📌 반복측정 분산분석 (repeated measures ANOVA)
- 동일한 대상에 대해 여러 번 반복측정하여 반복측정 집단 간에 차이가 존재하는지 검정
- 일반적 형태의 분산분석은 다른 집단에 속한 대상들 간의 집단 간 차이를 검정하는 반면에 반복측정 분산분석은 동일한 대상에 대한 검정이다.
CO2
식물이 저온 성장환경에서 견디는 정도
- Quebec 지역 나무와 Mississippi 지역 나무 간의 이산화탄소 흡수율에 따라 차이가 있는지 검정
- 7개의 서로 다른 이산화탄소 농도에 따라 흡수율에 차이가 있는지 검정
- 나무 출신 지역과 이산화탄소 읍수율의 관계가 농도에 따라 달라지는지 검정
- uptake (종속변수) : 이산화탄소 흡수율
- Type (독립변수), conc (독립변수) : 나무의 출신 지역, 이산화탄소 농도
- Type (집단 간 요인)
- conc (집단 내 요인) => 반복적으로 측정된 값
- Treatment : 저온처리 여부
- Plant : 나무의 고유 식별
>str(CO2)
Classes ‘nfnGroupedData’, ‘nfGroupedData’, ‘groupedData’ and 'data.frame': 84 obs. of 5 variables:
$ Plant : Ord.factor w/ 12 levels "Qn1"<"Qn2"<"Qn3"<..: 1 1 1 1 1 1 1 2 2 2 ...
$ Type : Factor w/ 2 levels "Quebec","Mississippi": 1 1 1 1 1 1 1 1 1 1 ...
$ Treatment: Factor w/ 2 levels "nonchilled","chilled": 1 1 1 1 1 1 1 1 1 1 ...
$ conc : num 95 175 250 350 500 675 1000 95 175 250 ...
$ uptake : num 16 30.4 34.8 37.2 35.3 39.2 39.7 13.6 27.3 37.1 ...
- attr(*, "formula")=Class 'formula' language uptake ~ conc | Plant
.. ..- attr(*, ".Environment")=<environment: R_EmptyEnv>
- attr(*, "outer")=Class 'formula' language ~Treatment * Type
.. ..- attr(*, ".Environment")=<environment: R_EmptyEnv>
- attr(*, "labels")=List of 2
..$ x: chr "Ambient carbon dioxide concentration"
..$ y: chr "CO2 uptake rate"
- attr(*, "units")=List of 2
..$ x: chr "(uL/L)"
..$ y: chr "(umol/m^2 s)"> CO2sub <- subset(CO2, Treatment == "chilled")
> CO2sub$conc <- factor(CO2sub$conc)
> str(CO2sub)
Classes ‘nfnGroupedData’, ‘nfGroupedData’, ‘groupedData’ and 'data.frame': 42 obs. of 5 variables:
$ Plant : Ord.factor w/ 12 levels "Qn1"<"Qn2"<"Qn3"<..: 4 4 4 4 4 4 4 6 6 6 ...
$ Type : Factor w/ 2 levels "Quebec","Mississippi": 1 1 1 1 1 1 1 1 1 1 ...
$ Treatment: Factor w/ 2 levels "nonchilled","chilled": 2 2 2 2 2 2 2 2 2 2 ...
$ conc : Factor w/ 7 levels "95","175","250",..: 1 2 3 4 5 6 7 1 2 3 ...
$ uptake : num 14.2 24.1 30.3 34.6 32.5 35.4 38.7 9.3 27.3 35 ..
> CO2sub
Plant Type Treatment conc uptake
22 Qc1 Quebec chilled 95 14.2
23 Qc1 Quebec chilled 175 24.1
24 Qc1 Quebec chilled 250 30.3
25 Qc1 Quebec chilled 350 34.6
26 Qc1 Quebec chilled 500 32.5
27 Qc1 Quebec chilled 675 35.4
28 Qc1 Quebec chilled 1000 38.7
29 Qc2 Quebec chilled 95 9.3
30 Qc2 Quebec chilled 175 27.3
31 Qc2 Quebec chilled 250 35.0
32 Qc2 Quebec chilled 350 38.8
33 Qc2 Quebec chilled 500 38.6
34 Qc2 Quebec chilled 675 37.5
35 Qc2 Quebec chilled 1000 42.4
36 Qc3 Quebec chilled 95 15.1
37 Qc3 Quebec chilled 175 21.0
38 Qc3 Quebec chilled 250 38.1
39 Qc3 Quebec chilled 350 34.0
40 Qc3 Quebec chilled 500 38.9
41 Qc3 Quebec chilled 675 39.6
42 Qc3 Quebec chilled 1000 41.4
64 Mc1 Mississippi chilled 95 10.5
65 Mc1 Mississippi chilled 175 14.9
66 Mc1 Mississippi chilled 250 18.1
67 Mc1 Mississippi chilled 350 18.9
68 Mc1 Mississippi chilled 500 19.5
69 Mc1 Mississippi chilled 675 22.2
70 Mc1 Mississippi chilled 1000 21.9
71 Mc2 Mississippi chilled 95 7.7
72 Mc2 Mississippi chilled 175 11.4
73 Mc2 Mississippi chilled 250 12.3
74 Mc2 Mississippi chilled 350 13.0
75 Mc2 Mississippi chilled 500 12.5
76 Mc2 Mississippi chilled 675 13.7
77 Mc2 Mississippi chilled 1000 14.4
78 Mc3 Mississippi chilled 95 10.6
79 Mc3 Mississippi chilled 175 18.0
80 Mc3 Mississippi chilled 250 17.9
81 Mc3 Mississippi chilled 350 17.9
82 Mc3 Mississippi chilled 500 17.9
83 Mc3 Mississippi chilled 675 18.9
84 Mc3 Mississippi chilled 1000 19.9📌 반복측정 분산분석
- 반복측정 일원분산분석 : y ~ W + Error(Subject/W)
- 반복측정 이원분산분석 : y ~ B * W + Error(Subject/W)
B는 집단 간 요인, W는 집단 내 요인을 의미하고,
Subject는 각 층정 대상에 대한 식별자 변수를 의미한다.
> CO2sub.aov <- aov(uptake ~ Type * conc + Error(Plant/conc), data=CO2sub)
> summary(CO2sub.aov)
Error: Plant
Df Sum Sq Mean Sq F value Pr(>F)
Type 1 2667.2 2667.2 60.41 0.00148 **
Residuals 4 176.6 44.1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: Plant:conc
Df Sum Sq Mean Sq F value Pr(>F)
conc 6 1472.4 245.40 52.52 1.26e-12 ***
Type:conc 6 428.8 71.47 15.30 3.75e-07 ***
Residuals 24 112.1 4.67
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Type 변수의 p-value가 유의하다. 귀무가설을 기각한다.
나무의 출신지역에 따라 이산화탄소의 흡수율이 다르다.
conc 변수의 p-value가 유의하다. 귀무가설을 기각한다.
이산화탄소 농소에 따라 이산화탄소의 흡수율이 다르다.
상호작용효과 Type:conc의 p-value가 유의하다. 귀무가설을 기각한다.나무 출신 지역과 이산화탄소 농도의 상호작용 효과가 존재한다.
> windows(width=12, height=8)
> boxplot(uptake ~ Type * conc, data=CO2sub,
+ col=c("deepskyblue", "violet"))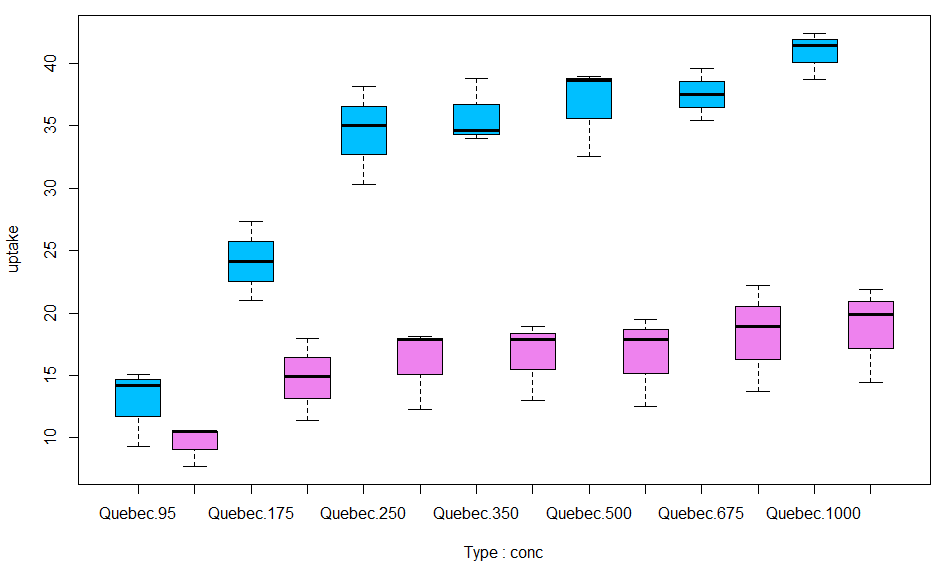
Quebec 나무에 대해서만 축이 나타나고 Mississippi에 대해서는 나타나지 않았다. 그래프를 좀 더 보기 좋게 다듬어 보자.
> boxplot(uptake ~ Type * conc, data=CO2sub,
+ col=c("deepskyblue", "violet"),
+ las=2, cex.axis=0.7,
+ xlab="", ylab="Carbon dioxide wptake rate",
+ main="Effects of Plant Type and CO2 on Carbon Dioxide uptake")
> legend("topleft", inset=0.02,
+ legend=c("Quebec", "Mississippi"),
+ fill=c("deepskyblue", "violet")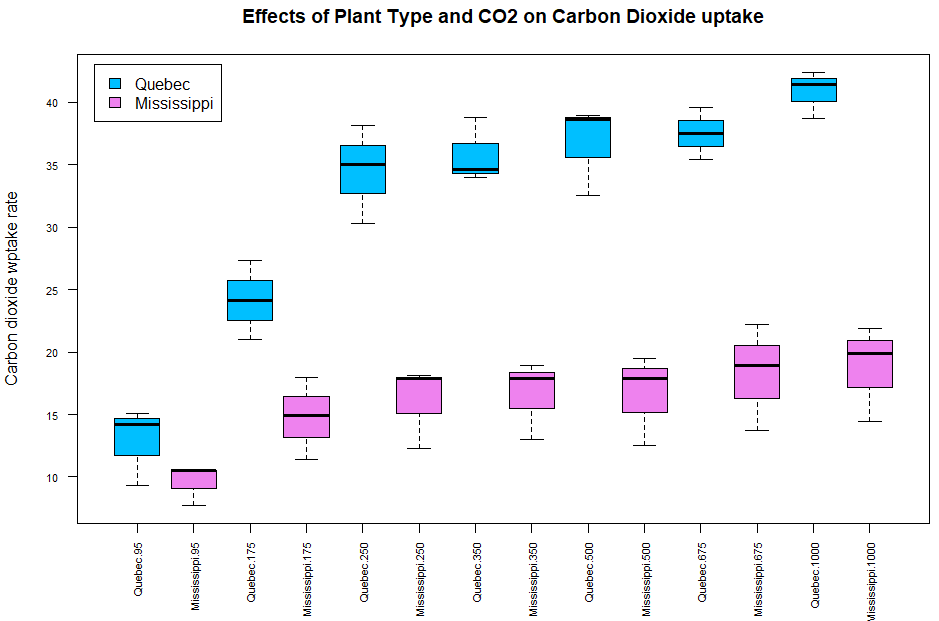
Quebec 나무가 Mississippi 나무보다 이산화탄소 흡수율이 높다.
이산화탄소 농도가 증가함에 따라 이산화탄소 흡수율도 증가한다.
> library(HH)
> interaction2wt(uptake ~ Type * conc, data=CO2sub)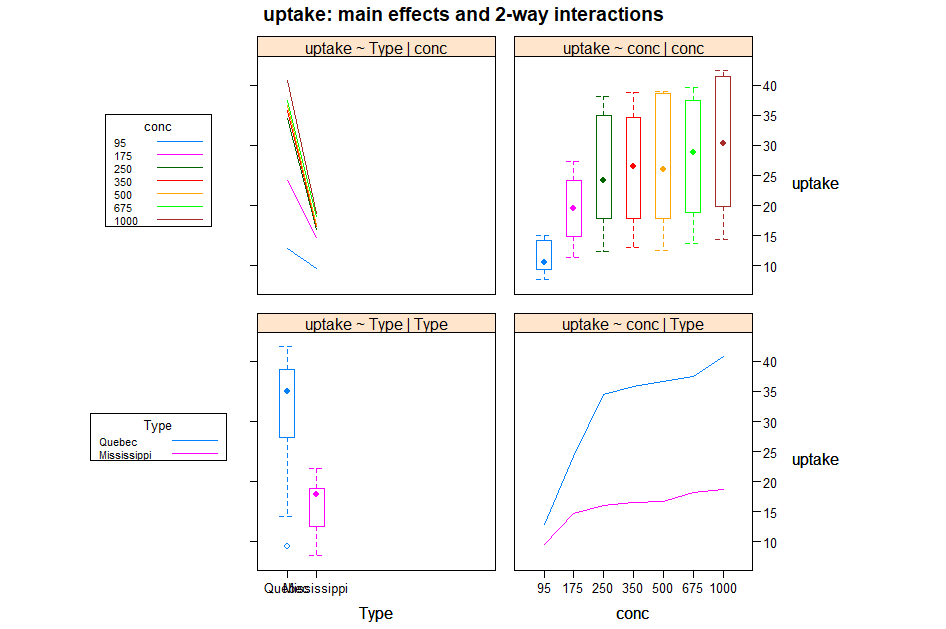
- 대각선 주효과
- 비대각선 상호작용효과
보다 신뢰할 만한 분석 결과를 얻기 위해서는 비록 동일한 대상에 대해 시점을 달리하여 반복적으로 측정된 데이터이긴 하지만, 모든 반복 차수 간의 관련성의 정도는 일정해야 한다.
구형성검정(sphericity test)을 통해 측정값 간 차이의 분산/공분산이 동일하다는 귀무가설을 검정할 수 있다.

반복측정 일원분산분석의 비모수 방법은 프리드만 검정으로 알고 있는데, 반복측정 이원분산분석에서의 비모수 방법은 검색해도 찾기 어렵습니다. 어떤 사이트에서는 반복측정 이원분산분석 방법 또한 프리드만 검정을 사용하라고 하는데, 변수 간에 교호작용 결과는 확인이 되지 않습니다. 순동님께서 올려주신 >CO2sub.aov <- aov(uptake ~ Type * conc + Error(Plant/conc), data=CO2sub) 와 같은 형태를 사용하는게 맞는 것 같은데, 제 데이터는 정규성을 만족하지 않아서 비모수 방법으로 사용해야 합니다ㅠ 프리드만 검정에서는 >friedman.test(count, groups = year, blocks = month) 이렇게 나와있어서 교호작용은 결과에서 확인이 안됩니다ㅠ 알려주시면 감사드리겠습니다.!!!