📌 분할 정복
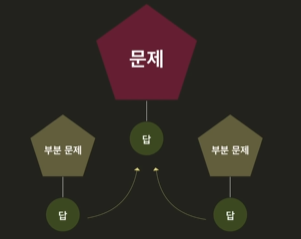
분할 정복은 3단계로 이루어진다.
예를 들어 함수 f(x)를 만들고 싶다고 가정하자. f는 파라미터로 x를 받는다.
- 분할(Divide)
문제를 부분 문제로 나눈다.
ex) x를 x1, x2으로 나눈다. - 정복(Conquer)
각 부분 문제를 정복한다.
ex) 부분 문제를 해결하기 위해 f(x1), f(x2)로 A, B라는 답이 나왔다. - 결합(Combine)
부분 문제들의 솔루션을 합쳐서 기존 문제를 해결한다.
ex) 두 솔루션 A, B를 이용해 기존 문제 f(x)를 해결한다.
만약 정복 단계가 A, B라는 답을 알아내기에 문제가 너무 크다면 정복 단계 안에서 또 분할, 정복, 결합 단계를 거친다.

📌 분할 정복 예시
✅ 1부터 100까지 더하는 문제를 분할 정복으로 풀어보자.
- 분할
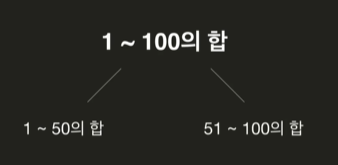
- 정복
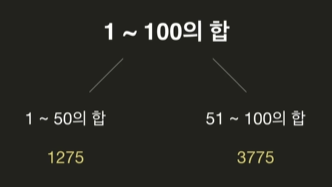
- 결합
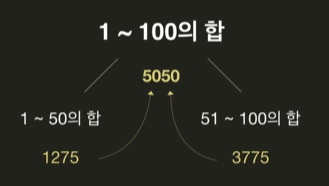
위 내용이 기본적인 방식이다. 내부적으로는 어떻게 동작할까❓
좀 더 간단하게 하기 위해 1부터 8까지의 합으로 변경한다.
✅ 1부터 8까지 더하는 문제를 분할 정복을 구해보자.
- 분할
- 1~4의 합과 5~8의 합으로 나눈다
- 정복
- 1~4의 합을 1~2의 합과 3~4의 합으로 또 다시 분할한다.
- 5~8의 합을 5~6의 합과 7~8의 합으로 또 다시 분할한다.
- 1~2의 합은 1, 2가 나오므로 더 이상 분할하지 않는다. 이렇게 문제가 충분히 작아진 경우를
Base Case라고 한다. 1 + 2 = 3 - 3~4의 합은 3, 4가 나오므로 더 이상 분할하지 않는다. 3 + 4 = 7
- 5~8의 합도 위와 같은 방식으로 진행한다.
- 결합
- 1~4의 합과 5~8의 합을 결합한다.
✅ 1부터 n까지의 합
분할 정복(Divide and Conquer)을 이용해서 1부터 n까지 더하는 예시를 보았다. 코드로 한 번 구현해 보자.
작성할 함수 consecutive_sum은 두 개의 정수 input start와 end를 받고, start부터 end까지의 합을 리턴한다. end는 start보다 크다고 가정한다.
💻 풀이
def consecutive_sum(start, end):
if start == end:
return start
else:
return consecutive_sum(start, (start + end) // 2) + consecutive_sum(((start + end) // 2) + 1, end)
print(consecutive_sum(1, 10)) # 55
print(consecutive_sum(1, 100)) # 5050
print(consecutive_sum(1, 253)) # 32131
print(consecutive_sum(1, 388)) # 75466📌 합병 정렬
📝 정렬 알고리즘
- 선택 정렬 (Selection Sort)
- 삽입 정렬 (Insertion Sort)
- 합병 정렬 (Merge Sort)
분할 정복을 사용하는 합병 정렬을 알아보자.
분할 정복은 세 단계로 나뉘며 합병 정렬에서의 분할 정복 단계는 다음과 같다.
분할 (Divide): 리스트를 반으로 나눈다.정복 (Conquer): 왼쪽 리스트와 오른쪽 리스트를 각각 정렬한다.결합 (Conbine): 정렬된 두 리스트를 하나의 정렬된 리스트로 합병한다.
결합 (Conbine) 부분을 자세히 살펴보자.

위와 같은 정렬된 두 리스트가 존재한다. 이를 어떻게 하나의 정렬된 리스트로 합칠 수 있을까 ❓



.
.
.

남은 왼쪽 리스트 값을 순서대로 정렬된 리스트에 넣어주면 완성된다.
📌 합병 정렬 진행 과정
아래의 리스트를 합병 정렬 방식으로 정렬해보자.

리스트를 반으로 나눈다.

나눠진 각 리스트를 또 다시 분할 단계로 반으로 나눈다.

아직도 리스트가 충분히 작지 않으므로 또 다시 재귀적으로 리스트를 반으로 나눈다.

리스트가 충분히 작아졌으므로 이를 정렬한다.
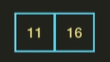
나머지 [6, 13] 리스트도 마찬가지로 분할하고 정렬한다.

이제 [11, 16]과 [6, 13]을 정렬하여 합쳐준다.

[1, 7, 10, 4] 리스트도 마찬가지로 위 과정을 반복하여 정렬하고 합쳐준다.


✅ 합병 정렬 구현
합병 정렬 알고리즘 중 사용되는 merge 함수를 작성하라.
merge 함수는 정렬된 두 리스트 list1과 list2를 받아서, 하나의 정렬된 리스트를 리턴한다.
Divide and Conquer 방식으로 merge_sort 함수를 작성하라. merge_sort는 파라미터로 리스트 하나를 받고, 정렬된 새로운 리스트를 리턴한다.
💻 풀이
def merge(list1, list2):
sorted_list = []
i = 0
j = 0
while len(list1) > i and len(list2) > j:
if list1[i] > list2[j]:
sorted_list.append(list2[j])
j += 1
else:
sorted_list.append(list1[i])
i += 1
if i == len(list1):
sorted_list += list2[j:]
if j == len(list2):
sorted_list += list1[i:]
return sorted_list
def merge_sort(my_list):
mid = len(my_list) // 2
if len(my_list) < 2:
return my_list
else:
return merge(merge_sort(my_list[:mid]), merge_sort(my_list[mid:]))
print(merge_sort([1, 3, 5, 7, 9, 11, 13, 11]))
print(merge_sort([28, 13, 9, 30, 1, 48, 5, 7, 15]))
print(merge_sort([2, 5, 6, 7, 1, 2, 4, 7, 10, 11, 4, 15, 13, 1, 6, 4]))👉 결과
[1, 3, 5, 7, 9, 11, 11, 13]
[1, 5, 7, 9, 13, 15, 28, 30, 48]
[1, 1, 2, 2, 4, 4, 4, 5, 6, 6, 7, 7, 10, 11, 13, 15]📌 퀵 정렬(Quicksort)
분할 정복을 사용하는 또 다른 정렬 알고리즘이 있다. 바로 퀵 정렬이다.

- 분할
퀵 정렬에서 리스트를 나누는 과정을Partition이라고 한다.
편의상 마지막 값을 pivot으로 정하였다.
pivot을 기준으로 더 작은 값은 왼쪽에, 더 큰 값은 오른쪽으로 배치한다.


- 정복
pivot 왼쪽 값과 오른쪽 값을 각각 정렬해준다.

- 결합
퀵 정렬은 결합 단계에서 딱히 할 게 없다.
분할과 정복 단계만 거치면 자동으로 정렬이 되어 있기 때문이다.
📌 퀵 정렬 진행 과정

위의 리스트로 퀵 정렬을 진행하려고 한다.
편의상 마지막 값을 pivot으로 정한다.

pivot인 7보다 작은 값들은 왼쪽에, 7보다 큰 값들은 오른쪽에 배치한다.
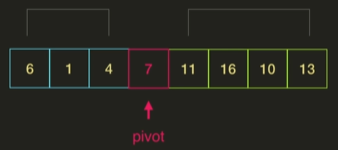
이제 pivot의 왼쪽과 오른쪽을 각각 정렬해주면 되는데, 이 과정에서 또 다시 분할, 정복 단계가 이루어진다.
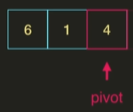
4를 pivot으로 정한다.
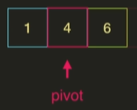
4보다 작은 값은 왼쪽에, 4보다 큰 값은 오른쪽에 배치한다.
왼쪽과 오른쪽에 값이 하나 밖에 없으므로 이미 정렬된 상태이다.
이 경우를 base case라고 한다.
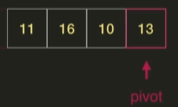
왼쪽의 정렬이 끝났으므로 오른쪽 정렬을 위해 또 다시 분할, 정복 단계를 진행한다.
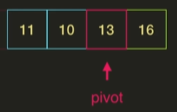
pivot인 13보다 작은 값은 왼쪽에, 13보다 큰 값은 오른쪽에 배치한다.
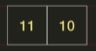
13의 왼쪽 부분에 또 다시 분할, 정복 단계를 진행한다.
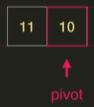
오른쪽에 값이 하나 밖에 없으므로 이미 정렬된 상태이다.
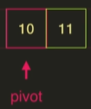
13의 왼쪽 부분은 정렬이 끝났으므로 오른쪽을 정렬한다.
그러나 13의 오른쪽 리스트도 base case이기 때문에 이미 정복을 완료했다.

다시 처음으로 돌아가면 pivot 7의 왼쪼과 오른쪽이 정렬이 되었다.

리스트 전체 정렬 되어 퀵 정렬은 끝이 난다.
📌 partition 함수 설명
퀵 정렬에서 가장 어려운 부분이 분할 단계이다.
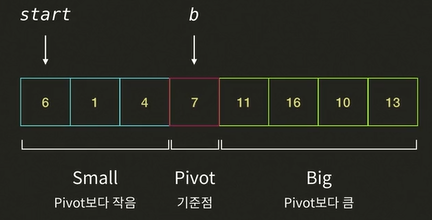
아래의 리스트를 partition 하려고 한다.


i: unknown이 시작되는 인덱스b: Big 그룹이 시작 되는 인덱스p: pivot
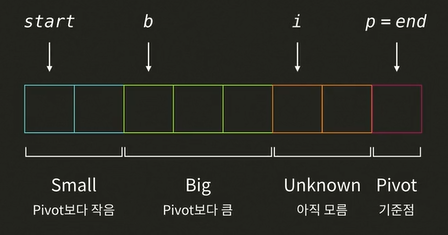
- 시작할 떈
i와b가 모두 가장 왼쪽 인덱스를 가르킨다. - 아무 값도 확인하지 않았으므로 모든 인덱스가
Unknown이다.
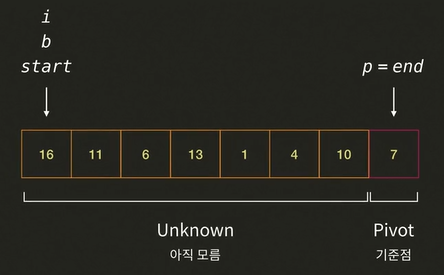
i가 가르키는 16을pivot7와 비교한다. 16 > 7 이므로 Big 그룹에 해당된다.- i가 오른쪽으로 한 칸 이동한다.
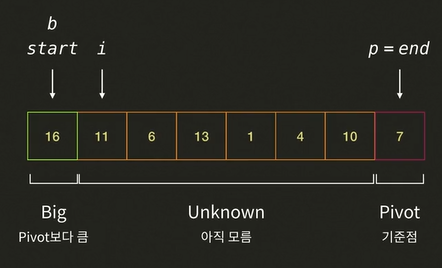
i가 가르키는 11과pivot7와 비교한다. 11 > 7 이므로 Big 그룹에 해당된다.- i가 오른쪽으로 한 칸 이동한다.

i가 가르키는 6을pivot7와 비교한다. 6 < 7 이므로 Small 그룹에 해당된다.i가 가르키는 6과b가 가르키는 16의 자리를 바꾼다.i와b를 모두 오른쪽으로 한 칸 이동한다.
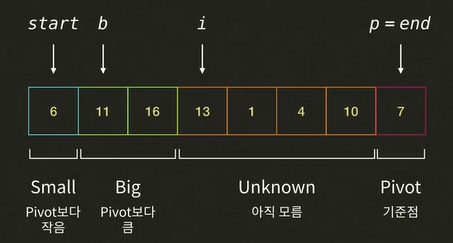
i가 가르키는 13과pivot7을 비교한다. 13 > 7 이므로 Big 그룹에 해당된다.i를 오른쪽으로 한 칸 이동한다.
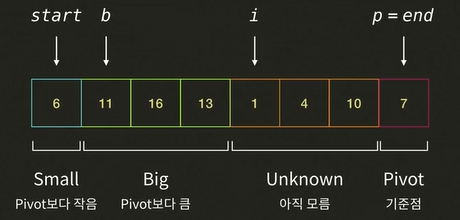
i가 가르키는 1과pivot7을 비교한다. 1 < 7 이므로 Small 그룹에 해당된다.i가 가르키는 1과b가 가르키는 11의 자리를 바꾼다.i와b를 모두 오른쪽으로 한 칸 이동한다.
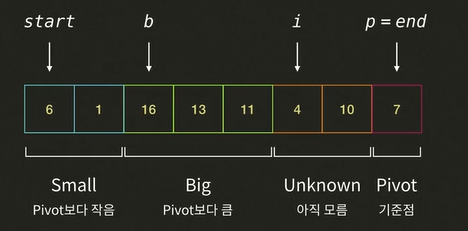
i가 가르키는 4와pivot7을 비교한다. 4 < 7 이므로 Small 그룹에 해당한다.i가 가르키는 4과b가 가르키는 16의 자리를 바꾼다.i와b를 모두 오른쪽으로 한 칸 이동한다.
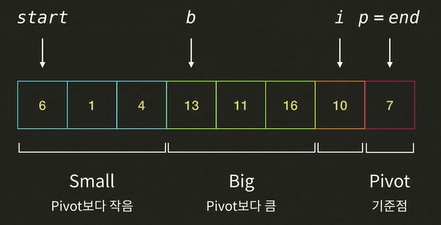
i가 가르키는 10과pivot7을 비교한다. 10 > 7 이므로 Big 그룹에 해당한다.i를 오른쪽으로 한 칸 이동한다.i가pivot에 도착한다.b가 가르키는 13과pivot이 가르키는 7의 자리를 바꾼다.pivot왼쪽에는 작은 값이,pivot오른쪽에는 큰 값이 들어가partition이 끝이 난다.
✅ partition 함수 구현
partiton 함수는 리스트 my_list, 그리고 partiton할 범위를 나타내는 인덱스 start와 end를 파라미터로 받는다. my_list의 값들을 pivot 기준으로 재배치한 후, pivot의 최종 위치 인덱스를 리턴한다.
💻 풀이
def swap_elements(my_list, index1, index2):
my_list[index1], my_list[index2] = my_list[index2], my_list[index1]
def partition(my_list, start, end):
i = start
b = start
p = end
while i < p:
if my_list[i] <= my_list[p]:
swap_elements(my_list, i, b)
b += 1
i += 1
if my_list[i] > my_list[p]:
i += 1
if i == p:
swap_elements(my_list, b, p)
p = b
return p
list1 = [4, 3, 6, 2, 7, 1, 5]
pivot_index1 = partition(list1, 0, len(list1) - 1)
print(list1)
print(pivot_index1)
list2 = [6, 1, 2, 6, 3, 5, 4]
pivot_index2 = partition(list2, 0, len(list2) - 1)
print(list2)
print(pivot_index2)👉 결과
[4, 3, 2, 1, 5, 6, 7]
4
[1, 2, 3, 4, 6, 5, 6]
3✅ 퀵 정렬 구현하기
분할 정복 방식으로 quicksort 함수를 작성하라.
quicksort는 파라미터로 리스트 하나와 리스트 내에서 정렬시킬 범위를 나타내는 인덱스 start와 인덱스 end를 받는다.
merge_sort 함수와 달리 quicksort 함수는 정렬된 새로운 리스트를 리턴하는 게 아니라, 파라미터로 받는 리스트 자체를 정렬시킨다.
💻 풀이
def swap_elements(my_list, index1, index2):
my_list[index1], my_list[index2] = my_list[index2], my_list[index1]
def partition(my_list, start, end):
i = start
b = start
p = end
while i < p:
if my_list[i] <= my_list[p]:
swap_elements(my_list, i, b)
b += 1
i += 1
if my_list[i] > my_list[p]:
i += 1
if i == p:
swap_elements(my_list, b, p)
p = b
return p
def quicksort(my_list, start, end):
if end - start < 1:
return
else:
p = partition(my_list, start, end)
quicksort(my_list, start, p-1)
quicksort(my_list, p+1, end)
return
list1 = [1, 3, 5, 7, 9, 11, 13, 11]
quicksort(list1, 0, len(list1) - 1)
print(list1)
list2 = [28, 13, 9, 30, 1, 48, 5, 7, 15]
quicksort(list2, 0, len(list2) - 1)
print(list2)
list3 = [2, 5, 6, 7, 1, 2, 4, 7, 10, 11, 4, 15, 13, 1, 6, 4]
quicksort(list3, 0, len(list3) - 1)
print(list3)👉 결과
[1, 3, 5, 7, 9, 11, 11, 13]
[1, 5, 7, 9, 13, 15, 28, 30, 48]
[1, 1, 2, 2, 4, 4, 4, 5, 6, 6, 7, 7, 10, 11, 13, 15]... ing
