📌 일원분산분석(one-way ANOVA)
집단을 구분하는 독립변수가 한 개일 때 모집단 간 평균의 동일성 검정
- 귀무가설 : 집단 간 평균은 모두 동일하다.
- 대립가설 : 집단 간 평균은 모두 동일하지 않다. (한 집단이라도 통계적으로 유의한 차이를 보인다면 귀무가설 기각)
> # 살충제에 대한 실험 데이터
> # count : 살아남은 해충의 개수, spray : 스프레이 변수
> str(InsectSprays)
'data.frame': 72 obs. of 2 variables:
$ count: num 10 7 20 14 14 12 10 23 17 20 ...
$ spray: Factor w/ 6 levels "A","B","C","D",..: 1 1 1 1 1 1 1 1 1 1 ...
> head(InsectSprays)
count spray
1 10 A
2 7 A
3 20 A
4 14 A
5 14 A
6 12 A
> # 집단별 표본 크기
> tapply(InsectSprays$count, InsectSprays$spray, length)
A B C D E F
12 12 12 12 12 12
> tapply(InsectSprays$count, InsectSprays$spray, mean) # 살충제별 평균
A B C D E F
14.500000 15.333333 2.083333 4.916667 3.500000 16.666667
> tapply(InsectSprays$count, InsectSprays$spray, sd) # 살충제별 표준편차
A B C D E F
4.719399 4.271115 1.975225 2.503028 1.732051 6.213378
> library(gplots)
> windows(width=12, height=8) # window 창 열기📌 집단 간 차이 그래프로 시각화
plotmeans()
plotmeans(종속변수 ~ 독립변수, data=)
집단별 평균과 평균에 대한 95% 신뢰구간 그래프
> plotmeans(count ~ spray, data=InsectSprays,
+ barcol ="tomato", barwidth=,
+ col="cornflowerblue", lwd=2,
+ xlab="Type of Sprays", ylab="Insect Count",
+ main="Performance of Insect Sprays")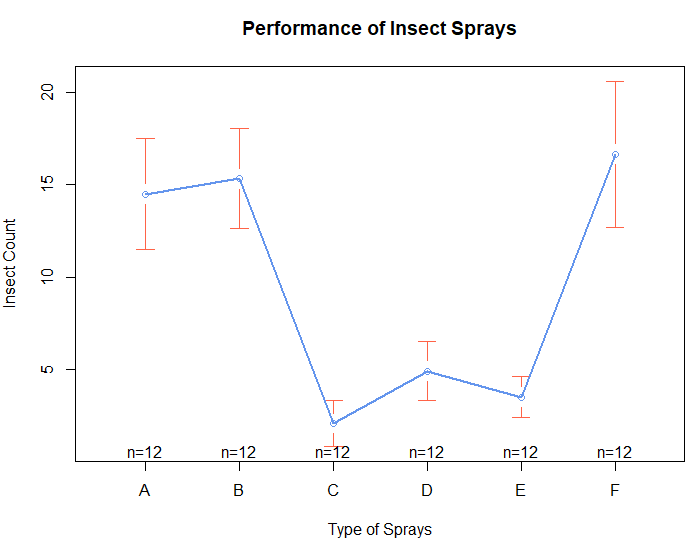
boxplot()
boxplot(종속변수 ~ 독립변수, data=)
> boxplot(count ~ spray, data=InsectSprays, col="tomato",
+ xlab="Type of Sprays", ylab="Insect Count",
+ main="Performance of Insect Sprays")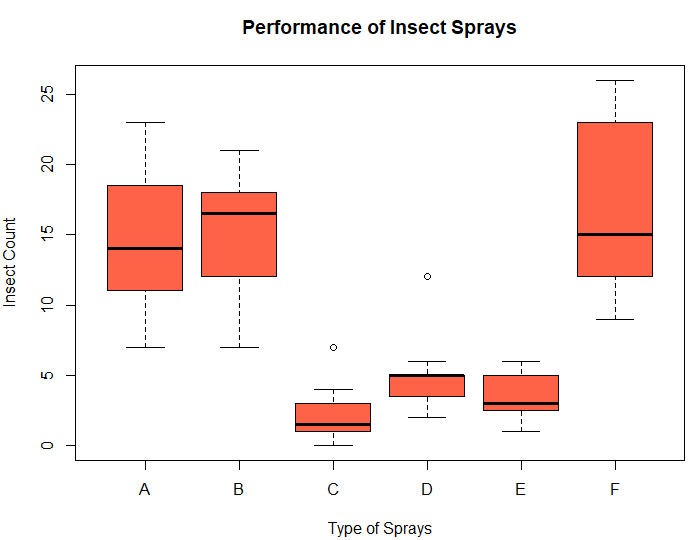
📌 분산분석(ANOVA)
aov(종속변수 ~ 독립변수, data=)
> spray.aov <- aov(count ~ spray, data=InsectSprays)
> spray.aov
Call:
aov(formula = count ~ spray, data = InsectSprays)
Terms:
spray Residuals
Sum of Squares 2668.833 1015.167
Deg. of Freedom 5 66
Residual standard error: 3.921902
Estimated effects may be unbalanced
> summary(spray.aov)
Df Sum Sq Mean Sq F value Pr(>F)
spray 5 2669 533.8 34.7 <2e-16 ***
Residuals 66 1015 15.4
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1귀무가설을 기각한다. 즉, 평균에 차이가 있다. 그러나 어떤 집단의 평균이 다른 건지는 알 수 없다.
어떤 집단 간에 차이가 있는가❓
model.tables
model.tables(분산분석 모델, type=c("mean", "effects")
개별 집단간 평균 차이 확인
# type="mean" 전체 평균과 함께 각 집단의 평균
> model.tables(spray.aov, type="mean")
Tables of means
Grand mean
9.5
spray
spray
A B C D E F
14.500 15.333 2.083 4.917 3.500 16.667
# type="effects" : 각 집단평균과 전체평균의 차이
> model.tables(spray.aov, type="effects")
Tables of effects
spray
spray
A B C D E F
5.000 5.833 -7.417 -4.583 -6.000 7.167 ⭐ 사후분석 ⭐
TukeyHSD()
터키 HSD 검정(Tukey HSD test)
통계적으로 유의미한 차이가 있는지를 검정한다.
> spray.compare <- TukeyHSD(spray.aov)
> spray.compare
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = count ~ spray, data = InsectSprays)
$spray
diff lwr upr p adj
B-A 0.8333333 -3.866075 5.532742 0.9951810
C-A -12.4166667 -17.116075 -7.717258 0.0000000
D-A -9.5833333 -14.282742 -4.883925 0.0000014
E-A -11.0000000 -15.699409 -6.300591 0.0000000
F-A 2.1666667 -2.532742 6.866075 0.7542147
C-B -13.2500000 -17.949409 -8.550591 0.0000000
D-B -10.4166667 -15.116075 -5.717258 0.0000002
E-B -11.8333333 -16.532742 -7.133925 0.0000000
F-B 1.3333333 -3.366075 6.032742 0.9603075
D-C 2.8333333 -1.866075 7.532742 0.4920707
E-C 1.4166667 -3.282742 6.116075 0.9488669
F-C 14.5833333 9.883925 19.282742 0.0000000
E-D -1.4166667 -6.116075 3.282742 0.9488669
F-D 11.7500000 7.050591 16.449409 0.0000000
F-E 13.1666667 8.467258 17.866075 0.0000000
> # 살충제 D와 C만 추출
> spray.compare$spray['D-C', ] # 두 살충제간 차이가 없다.
diff lwr upr p adj
2.8333333 -1.8660752 7.5327418 0.4920707
> plot(spray.compare, col="blue", las=1)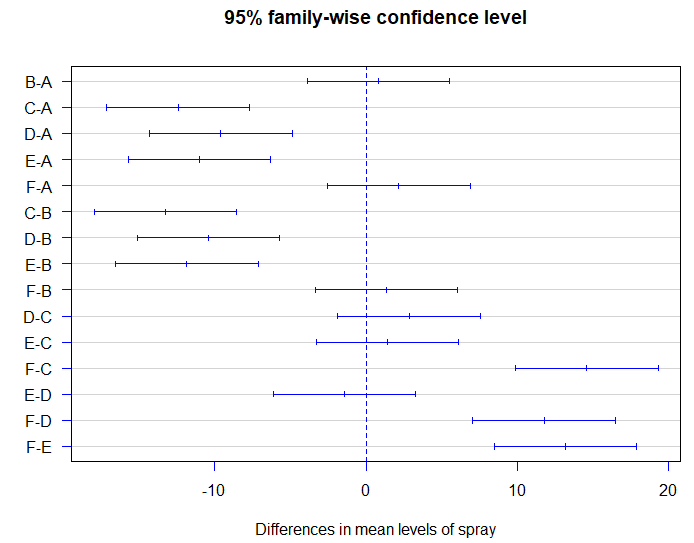
가로선은 집단 간 평균의 차이에 대한 신뢰구간을 나타내며, 0을 포함하지 않으면 통계적으로 유의하다.
glht()
glht() 이용해 TukeyHSD 검정 수행
glht(model=모델 객체, linfct=검정할 가설)
> library(multcomp)
> tuk.hsd <- glht(model=spray.aov, linfct=mcp(spray="Tukey"))
> tuk.hsd
General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Linear Hypotheses:
Estimate
B - A == 0 0.8333
C - A == 0 -12.4167
D - A == 0 -9.5833
E - A == 0 -11.0000
F - A == 0 2.1667
C - B == 0 -13.2500
D - B == 0 -10.4167
E - B == 0 -11.8333
F - B == 0 1.3333
D - C == 0 2.8333
E - C == 0 1.4167
F - C == 0 14.5833
E - D == 0 -1.4167
F - D == 0 11.7500
F - E == 0 13.1667
> cld(tuk.hsd, level=0.05)
A B C D E F
"b" "b" "a" "a" "a" "b"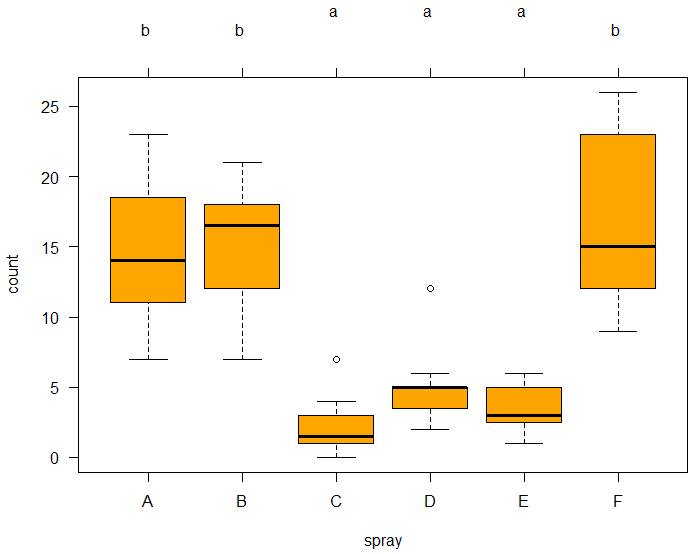
A, B, F의 평균이 같고, C, D, E의 평균이 같다.
📌 분산분석의 가정
- 정규성 : 종속변수는 정규분포를 따른다.
- 등분산성 : 각 집단의 분포는 모두 동일한 분산을 가진다.
정규성
qqplot(data vector, id=)
> library(car)
> plot(cld(tuk.hsd, level=0.05), col="orange", las=1)
> qqPlot(InsectSprays$count, id=FALSE, pch=20, col="deepskyblue",
+ xlab="Theoretical Quantiles", ylab="Empirical Quantiles",
+ main="Q-Q Plot")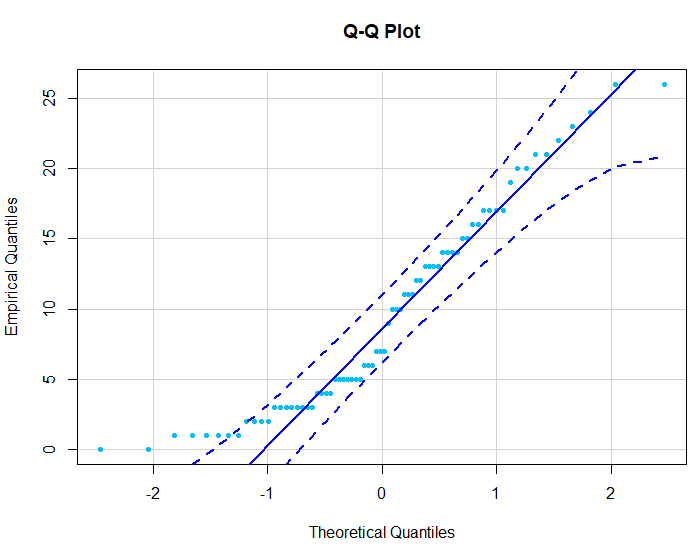
> shapiro.test(InsectSprays$count)
Shapiro-Wilk normality test
data: InsectSprays$count
W = 0.9216, p-value = 0.0002525정규성 가정을 만족하지 못한다.
이상점
car 패키지의 outlietTest() 함수
> outlierTest(spray.aov)
No Studentized residuals with Bonferroni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferroni p
69 2.590966 0.011804 0.8499Bonferroni p > 0.05 이면 이상점이 존재하지 않는다.
등분산성
car 패키지의 leveneTest() 함수 or stats 패키지의 bartlett.test() 함수
> leveneTest(count ~ spray, data=InsectSprays)
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 3.8214 0.004223 **
66
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> bartlett.test(count ~ spray, data=InsectSprays)
Bartlett test of homogeneity of variances
data: count by spray
Bartlett's K-squared = 25.96, df = 5, p-value = 9.085e-05귀무가설을 기각하므로 등분산성을 만족하지 못 한다.
📌 등분산 가정 O : aov()
> summary(aov(count ~ spray, data=InsectSprays))
Df Sum Sq Mean Sq F value Pr(>F)
spray 5 2669 533.8 34.7 <2e-16 ***
Residuals 66 1015 15.4
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1📌 등분산 가정 X : oneway.test()
> oneway.test(count ~ spray, data=InsectSprays)
One-way analysis of means (not assuming equal variances)
data: count and spray
F = 36.065, num df = 5.000, denom df = 30.043, p-value = 7.999e-12📌 등분산 가정 O : equal=TRUE
> oneway.test(count ~ spray, data=InsectSprays,var.equal=TRUE)
One-way analysis of means
data: count and spray
F = 34.702, num df = 5, denom df = 66, p-value < 2.2e-16등분산 가정을 만족하지 못 한다.
따라서 이번 데이터셋의 경우 oneway.test() 함수로 일원분산분석을 수행하는 것이 더 적절해 보인다.
