📌 카이스퀘어 검정(Chi-Square Test)
독립변수가 범주형인 표본인 모집단의 분포와 같은지 다른지 검정
- 독립성 검정 : 두 변수가 서로 연관이 있는가?
- 적합성 검정 : 모집단이 특정한 분포를 따르는지 판단하는 검정
- 관측빈도 : 교차표상의 실제 빈도
- 기대빈도 : 변수 간 서로 관련성이 없을 때 기대할 수 있는 예상빈도
- 자유도 = (행 범주 개수 - 1) * (열 범주 개수 - 1)
- 카이스퀘어 = (관측빈도 - 기대빈도)^2 / 기대빈도
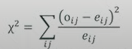
카이스퀘어 값이 크면 클수록 귀무가설을 기각한다.
# 안전벨트 착용과 승객 안전과의 관계
> survivors <- matrix(c(1443, 151, 47, 1781, 312, 135), ncol=2)
> dimnames(survivors) <- list(Status=c("minor injury", "major injury", "dead"),
Seatbelt=c("with seatbelt", "without seatbelt"))
> survivors
Seatbelt
Status with seatbelt without seatbelt
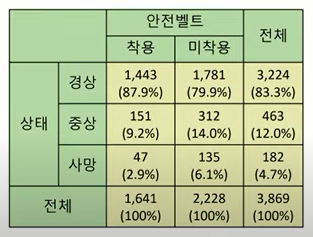
minor injury 1443 1781
major injury 151 312
dead 47 135
> addmargins(prop.table(addmargins(survivors, 2), 2), 1)
Seatbelt
Status with seatbelt without seatbelt Sum
minor injury 0.87934186 0.79937163 0.83329026
major injury 0.09201706 0.14003591 0.11966917
dead 0.02864107 0.06059246 0.04704058
Sum 1.00000000 1.00000000 1.00000000
> windows(width=7.0, height=5.5)
> barplot(survivors, ylim=c(0, 2500), las=1,
+ col=c("yellowgreen", "lightsalmon", "orangered"),
+ ylab="Frequency", main="Frequency of Survivoirs")
> legend(0.2, 2500, rownames(survivors),
+ fill=c("yellowgreen", "lightsalmon", "orangered"))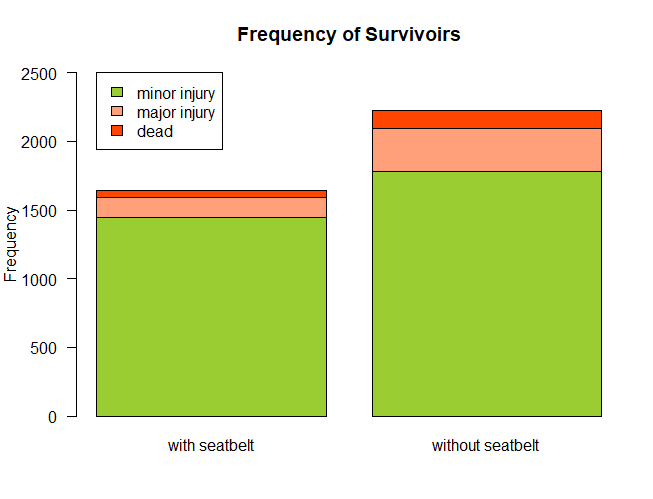
> survivors.prop <- prop.table(survivors, 2)
> barplot(survivors.prop*100, las=1,
+ col=c("yellowgreen", "lightsalmon", "orangered"),
+ ylab="Percent", main="Percent of Survivoirs")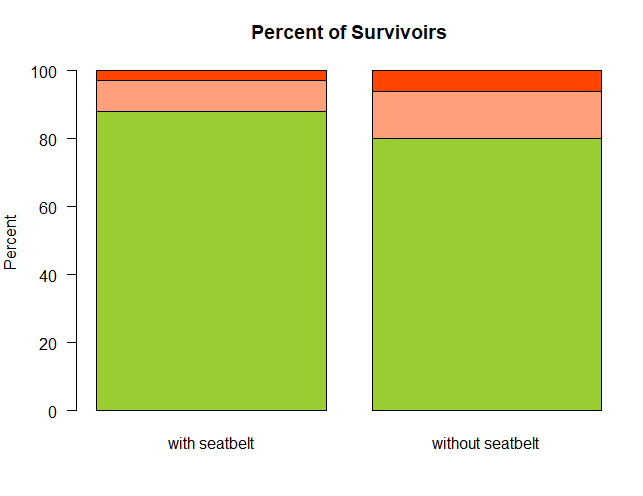
📌 통계적 검정
- 관측된 카이스퀘어 검정통계량의 유의확률(p-value)
- 유의수준 하에서의 카이스퀘어 검정통계량을 구한 후 관측된 카이스퀘어 검정통계량과 비교
관측된 카이스퀘어 값이 더 크면 귀무가설을 기각한다.

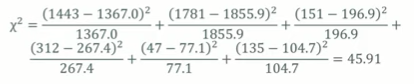
> # 유의확률
> pchisq(45.91, df=(3-1)*(2-1), lower.tail=FALSE)
[1] 1.073421e-10
> # 카이스퀘어 값
> qchisq(0.05, df=(3-1)*(2-1), lower.tail=FALSE)
[1] 5.99146귀무가설을 기각한다. 안전벨트 착용 유무는 환자의 상태와 관련이 있다.
