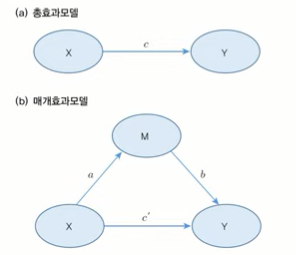
📌 매개효과분석
- 첫 번째 변수 X가 두 번째 변수 M에 영향을 미치고, 이어서 차례로 그 변수가 세 번쩨 변수 Y에 영향을 미치는 연쇄적인 영향 관계를 검정한다.
- 두 변수 X와 Y사이에서 일련의 영향관계가 어떠한 과정을 거쳐 발생하는지 설명하는 변수 M을 매개변수(mediator)라고 한다.
- 매개효과는 간접효과(indirect effect)라고도 한다.
- c'=0이면 완전매개(perfect mediation)
- c > c'이면 부분매개(paritial mediation)
- c : 총효과
- c' : 직접효과
- ab : 간접효과(매개효과)
- c = c' + ab (총효과 = 직접효과 + 간접효과)
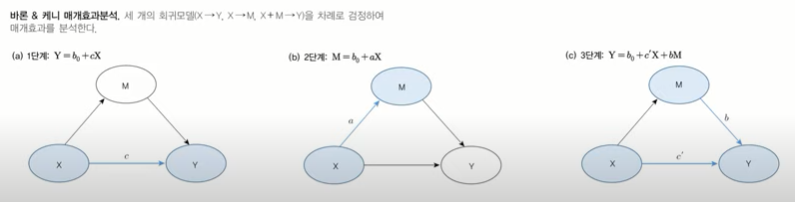
📌 바론 & 케니 매개효과분석
간접효과에 대한 통계적 검정 결과를 제시하지 않기 때문에 따로 검정이 필요하다.
- 1단계 : Y = b0 + cX : c가 통계적으로 유의한지 검정
- 2단계 : M = b0 + aX : a가 통계적으로 유의한지 검정
회귀계수 a는 통계적으로 유의해야 한다. X와 M간의 어떠한 유의적 관계가 없으면 M은 매개변수가 아니라 Y에 대한 제 3의 독립변수가 되기 때문이다.
- 3단계 : Y = b0 + c'X + bM : X를 통제한 후에 M과 Y와의 관계를 검정, b가 통계적으로 유의해야 한다.
📝 ex) mtcars 데이터 셋
- 1단계 : mpg ~ disp
- 2단계 : wt ~ disp
- 3단계 : mpg ~ disp + wt
> str(mtcars)
'data.frame': 32 obs. of 11 variables:
$ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
$ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
$ disp: num 160 160 108 258 360 ...
$ hp : num 110 110 93 110 175 105 245 62 95 123 ...
$ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
$ wt : num 2.62 2.88 2.32 3.21 3.44 ...
$ qsec: num 16.5 17 18.6 19.4 17 ...
$ vs : num 0 0 1 1 0 1 0 1 1 1 ...
$ am : num 1 1 1 0 0 0 0 0 0 0 ...
$ gear: num 4 4 4 3 3 3 3 4 4 4 ...
$ carb: num 4 4 1 1 2 1 4 2 2 4 ...> model.total <- lm(mpg ~ disp, data=mtcars)
> summary(model.total)
Call:
lm(formula = mpg ~ disp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-4.8922 -2.2022 -0.9631 1.6272 7.2305
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.599855 1.229720 24.070 < 2e-16 ***
disp -0.041215 0.004712 -8.747 9.38e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.251 on 30 degrees of freedom
Multiple R-squared: 0.7183, Adjusted R-squared: 0.709
F-statistic: 76.51 on 1 and 30 DF, p-value: 9.38e-10독립변수 disp의 p-value=9.38e-10이므로 disp는 mpg에 유의한 영향을 미친다. disp가 mpg에 미치는 총 효과(c)는 회귀계수인 -0.041215이다.
model.m <- lm(wt ~ disp, data=mtcars)
> summary(model.m)
Call:
lm(formula = wt ~ disp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-0.89044 -0.29775 -0.00684 0.33428 0.66525
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.5998146 0.1729964 9.248 2.74e-10 ***
disp 0.0070103 0.0006629 10.576 1.22e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4574 on 30 degrees of freedom
Multiple R-squared: 0.7885, Adjusted R-squared: 0.7815
F-statistic: 111.8 on 1 and 30 DF, p-value: 1.222e-11독립변수 disp의 p-value=1.22e-11이므로 disp는 wt와 유의한 영향 관계를 갖는다.
model.y <- lm(mpg ~ disp + wt, data=mtcars)
> summary(model.y)
Call:
lm(formula = mpg ~ disp + wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.4087 -2.3243 -0.7683 1.7721 6.3484
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.96055 2.16454 16.151 4.91e-16 ***
disp -0.01773 0.00919 -1.929 0.06362 .
wt -3.35082 1.16413 -2.878 0.00743 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.917 on 29 degrees of freedom
Multiple R-squared: 0.7809, Adjusted R-squared: 0.7658
F-statistic: 51.69 on 2 and 29 DF, p-value: 2.744e-10disp의 p-value=0.06362 통계적으로 유의하지 않다.
wt의 p-value=0.00743으로 통계적으로 유의하다.
매개효과 모델에서 disp와 mpg간의 직접효과는 존재하지 않는다.
1단계 모델에서는 disp와 mpg간의 총 효과가 존재하는 반면에 3단계 모델에서는 wt라는 매개변수의 투입으로 인해서 disp와 mpg간의 직접효과가 사라진다. 따라서 wt는 disp와 mpg간의 관계를 완전매개한다.
📌 간접효과
- 간접효과 = 독립변수와 매개변수 간의 회귀계수 * 매개변수와 종속변수 간의 회귀계수
- 독립변수와 매개변수 간의 회귀계수
2단계 모델에서 확인 가능 = 0.0070103- 매개변수와 종속변수 간의 회귀계수
3단계 모델에서 확인 가능 = -3.35082
> print(0.0070103 * (-3.35082))
[1] -0.02349025따라서 간접효과는 -0.0249025이다.
하지만 이 방법은 간접효과의 통계적 유의성을 검정해주지는 않는다.
📌 간접효과의 통계적 유의성 검정하는 방법 2가지
소벨(Sobel)검정
소벨검정은 매개변수 M이 존재할 때 독립변수 X가 종속변수 Y에 미치는 영향이 통계적으로 유의하게 감소하는지를 검정한다.
- 매개효과의 유의성 검정한다.
- 간접효과가 정규분포를 따라야하고, 표본 크기가 상대적으로 커야 한다는 제한이 있다.
cober(pred=독립변수, med=매개변수, out=종속변수)
> library(multilevel)
> model.sob <- sobel(pred=mtcars$disp, med=mtcars$wt, out=mtcars$mpg)
> model.sob
$`Mod1: Y~X`
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.59985476 1.229719515 24.070411 3.576586e-21
pred -0.04121512 0.004711833 -8.747152 9.380327e-10
$`Mod2: Y~X+M`
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.96055404 2.164539504 16.151497 4.910746e-16
pred -0.01772474 0.009190429 -1.928609 6.361981e-02
med -3.35082533 1.164128079 -2.878399 7.430725e-03
$`Mod3: M~X`
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.599814597 0.1729964404 9.247673 2.737804e-10
pred 0.007010325 0.0006628588 10.575896 1.222320e-11
$Indirect.Effect
[1] -0.02349038
$SE
[1] 0.008457775
$z.value
[1] -2.777371
$N
[1] 32z.value=-2.777371이다.
> pnorm(abs(model.sob$z.value), lower.tail=FALSE) * 2
[1] 0.005480063p-value=0.005480063으로 유의하기 때문에 매개효과가 존재한다.
또 다른 방법
> library(bda)
> mediation.test(mv=mtcars$wt, iv=mtcars$disp, dv=mtcars$mpg)p.value=0.005480063이므로 통계적으로 유의하다.
disp과 mpg의 관계는 wt에 대해서 유의하게 매개된다는 간접효과를 확인했다.
bootsprapping 검정
- 정규성 가정에 자유롭지 못하거나 상대적으로 작은 표본 크기에 사용 가능하다.
- 다수의 무작위 표본을 생성하여 간접효과를 추정하고 통계적 유의성을 검정한다.
> library(mediation)
> model.M <- lm(wt ~ disp, data=mtcars)
> model.Y <- lm(mpg ~ disp + wt, data=mtcars)
> set.seed(123)
> model.mediation <- mediate(model.m=model.M,
+ model.y=model.Y,
+ treat="disp",
+ mediator="wt",
+ boot=TRUE, sims=500)
> summary(model.mediation)매개변수 모델, 종속변수 모델, 독립변수, 매개변수, sims=추출한 표본 개수(기본값은 1000)

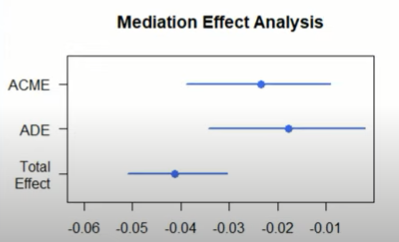
- Total Effect : 총효과
- ADE : 직접효과
- ACME : 매개효과(간접효과) = 총효과 - 직접효과
간접효과를 추정하고 이에 대한 통계적 유의성 검정이 목표이다.
ACME의 p-value=0.004이므로 매개효과는 존재한다.
총효과에 비해서 직접효과가 절댓값으로 크기가 더 작다.
따라서 wt는 disp와 mpg와의 관계를 부분매개한다.
> plot(model.mediation, cex=1.2, col="royalblue", lwd=2,
main="Mediation Effect Analysis")