📌 조절효과분석(moderation effect analysis)
- 변수 X와 변수 Y간 관계에 대한 제 3의 변수 Z의 영향을 검정한다.
- 제 3의 변수가 언제 어떤 조건하에서 두 변수 간 관계에 영향을 미치는지 검정하며, 변수
Z를조절변수(moderator)라고 한다. - 조절변수는 두 변수 간의 관계를 강화시키거나 약화시키며, 때로는 관계의 방향을 바꾸기도 한다.
- 조절효과는
상호작용효과(interaction effect)라고도 한다.
📝 ex) 자신감의 조절효과 : 시험의 중요도 vs 불안감
- x (독립변수) : 시험의 중요도
- y (종속변수) : 시험에 따른 불안감
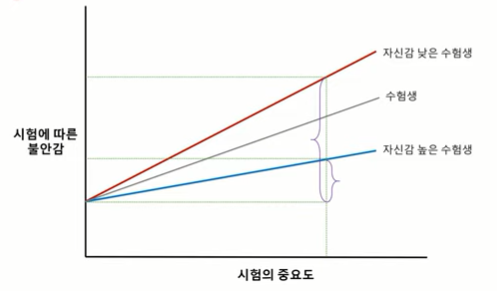
- 두 변수 간의 관계는 양의 선형관계를 갖는다.
- 시험의 중요도가 클수록 불안감은 증가한다.
- 중요도가 낮은 시험에 대해서는 모두 낮은 불안감을 느끼지만, 중요도가 높은 시험에 대해서는 자신감이 낮은 수험생이 더 많은 불안감을 느낀다.
- 이러한 현상을 자신감은 독립변수인 시험의 중요도와 상호작용한다고 한다.
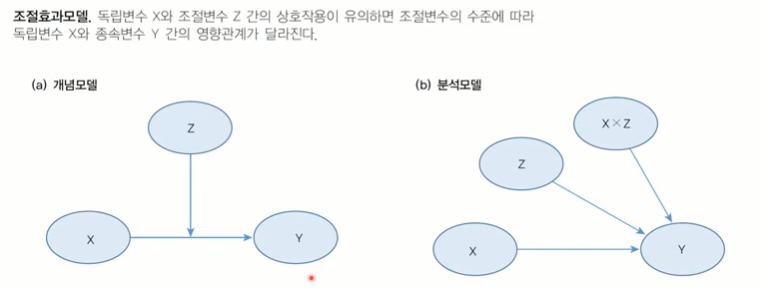
조절변수 Z가 변화함에 따라 독립변수 X가 종속변수 Y에 미치는 영향이 달라지는지를 검정한다.
- X x Y인 상호작용항이 종속변수에 미치는 영향이 유의하지 않다면, Z가 변화하더라도 X와 Y는 달라지지 않음을 의미한다.
- X x Y인 상호작용항이 종속변수에 미치는 영향이 유의하다면, Z가 변화함에 따라 X와 Y는 달라짐을 의미한다.
hp와 mpg의 관계에 있어서 wt가 조절변수 역할을 하는가❓
> str(mtcars)
'data.frame': 32 obs. of 11 variables:
$ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
$ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
$ disp: num 160 160 108 258 360 ...
$ hp : num 110 110 93 110 175 105 245 62 95 123 ...
$ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
$ wt : num 2.62 2.88 2.32 3.21 3.44 ...
$ qsec: num 16.5 17 18.6 19.4 17 ...
$ vs : num 0 0 1 1 0 1 0 1 1 1 ...
$ am : num 1 1 1 0 0 0 0 0 0 0 ...
$ gear: num 4 4 4 3 3 3 3 4 4 4 ...
$ carb: num 4 4 1 1 2 1 4 2 2 4 ...
- 독립변수 : hp (마력)
- 종속변수 : mpg (연비)
- 조절변수 : wt (무게)
mpg ~ hp + wt + hp:wt
> mtcars.lm <- lm(mpg ~ hp + wt + hp:wt, data=mtcars)
> summary(mtcars.lm)
Call:
lm(formula = mpg ~ hp + wt + hp:wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.0632 -1.6491 -0.7362 1.4211 4.5513
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.80842 3.60516 13.816 5.01e-14 ***
hp -0.12010 0.02470 -4.863 4.04e-05 ***
wt -8.21662 1.26971 -6.471 5.20e-07 ***
hp:wt 0.02785 0.00742 3.753 0.000811 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.153 on 28 degrees of freedom
Multiple R-squared: 0.8848, Adjusted R-squared: 0.8724
F-statistic: 71.66 on 3 and 28 DF, p-value: 2.981e-13hp:wt의 p-value=0.000811이므로 통계적으로 유의하다. 즉, 상호작용이 존재한다. hp와 mpg의 관계는 wt에 따라서 달라진다.
회귀식 : mpg = 49.808 - 0.120 x hp - 8.217 x wt + 0.028 x hp x wt
> round(mean(mtcars$wt), 1)
[1] 3.2
> round(sd(mtcars$wt), 1)
[1] 1평균은 3.2, 표준편차는 1이므로 평균을 중심으로 3개의 데이터를 만든다면, 2.2, 3.2, 4.2를 만들고, 이를 회귀식에 대입한다.
- w=2.3 : 31.731 - 0.058 x hp
- wt=3.2 : 23.514 - 0.030 x hp
- wt=4.2 : 15.297 - 0.002 x hp
wt가 증가함에 따라 hp의 증가가 mpg의 감소에 미치는 영향은 점차 작아진다. 따라서 hp와 mpg와의 관계는 wt에 따라 변화한다는 조절효과를 확인했다.
📌 상호작용 그래프로 시각화
- plot(effect(term=모델에서 시각화할 부분 포뮬러, mod=lm에서 반환된 조절효과 회귀모델, xlevels=일정하게 유지할 변수명과 변수값))
- multiline=TRUE : 하나의 그래프 창에 선들이 겹쳐서 나타남
> library(effects)
> m <- round(mean(mtcars$wt), 1)
> s <- round(sd(mtcars$wt), 1)
> m;s
[1] 3.2
[1] 1
> windows(width=, height=)
> plot(effect(term='hp:wt', mod=mtcars.lm, xlevels=list(wt=c(m-s, m, m+s))),
+ lines=list(multiline=TRUE, lwd=2, lty=c(3, 2, 1), col=c('royalblue', 'violet', 'maroon')),
+ main='Interaction Plot for Horsepower and Weight')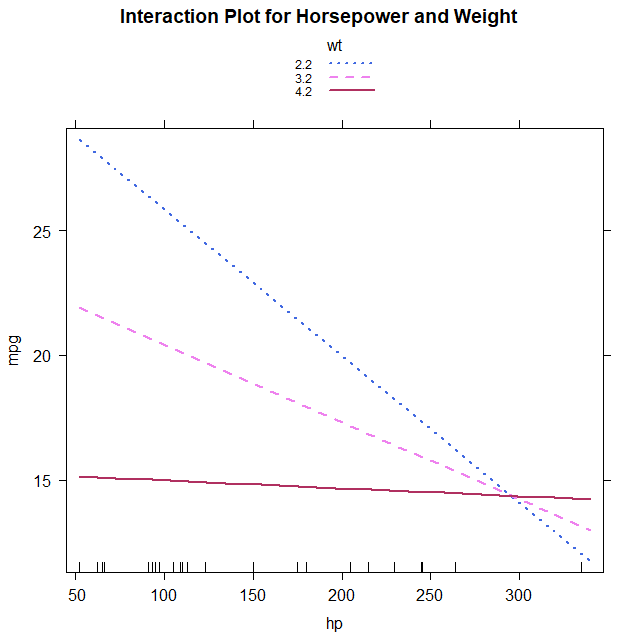
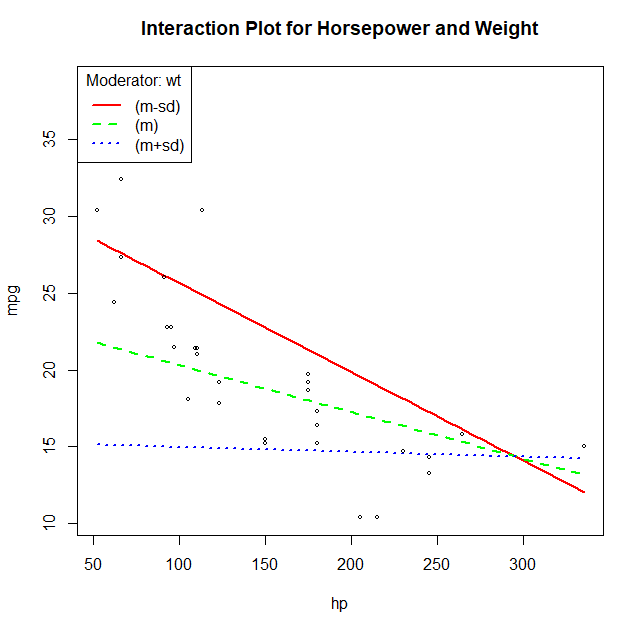
wt가 증가함에 따라 hp와 mpg의 관계가 약해지고 있다. => 기울기가 점점 작아진다.
plotSlpoes(model=조절효과 회귀모델, plotx='독립변수', modx='조절변수', modxVals=일정하게 유지할 조절변수 값)
> library(rockchalk)
> plotSlopes(model=mtcars.lm, plotx='hp', modx='wt',
+ modxVals='std.dev.', col=rainbow(3),
+ main='Interaction Plot for Horsepower and Weight')