[책 정리] Chapter 08. 우선순위 큐

yj 0·2022년 5월 24일

자료구조

목록 보기

8/12

8.1 우선순위 큐 추상 자료형

우선순위 큐의 소개

우선순위 큐(priority queue): 데이터들이 우선순뤼를 가지고 있고, 우선순위가 높은 데이터가 먼저 나가게 됨

자료구조	삭제되는 요소
스택	가장 최근에 들어온 데이터
큐	가장 먼저 들어온 데이터
우선순위 큐	가장 우선순위가 높은 데이터

우선순위 큐의 추상 자료형

<ADT 8.1.1> 우선순위 큐

객체: n개의 element 형의 우선순위를 가진 요소들의 모임
연산:
	create() ::= 우선순위 큐를 생성
    init(q) ::= 우선순위 큐 q를 초기화
    is_empty(q) ::= 우선순위 큐 q가 비어있는지 검사
    is_full(q) ::= 우선순위 큐 q가 가득찼는지 검사
    insert(q,x) ::= 우선순위 큐 q에 요소 x를 추가
    delete(q) ::= 우선순위 큐 q로부터 가장 우선순위가 높은 요소를 삭제하고 이 요소를 반환
    find(q) ::= 우선순위가 가장 높은 요소를 반환

Quiz

왜 우선순위 큐가 가장 일반적인 큐라고 할 수 있는가?
-> 스택이나 큐도 우선순위 큐를 사용하여 얼마든지 구현할 수 있기 때문
스택이나 큐도 우선순위 큐로 구현할 수 있는가?
-> 적절한 우선순위만 부여하면 우선순위 큐는 스택이나 큐로 동작함. 데이터가 들어온 시각을 우선순위로 잡으면 일반적인 큐 처럼 동작

8.2 우선순위 큐의 구현 방법

배열을 사용하는 방법

정렬이 안된 배열일 때

삽입 => 기존의 요소들의 맨 끝에 붙이면 됨(시간복잡도 $O(1)$ )
삭제(가장 우선순위가 높은 요소를 삭제) => 처음부터 끝까지 모든 요소들을 스캔해야 삭제 가능(시간복잡도 $O(n)$ ), 삭제 후 뒤에 있는 요소를 앞으로 이동시켜야 하는 부담이 있음

정렬이 되어 있는 배열일 때

삽입 => 일일이 다른 요소와 비교하여 우선순위에 따라 삽입 위치(순차 탐색, 이진 탐색)를 결정해야 함,그 후 삽입 위치 뒤에 있는 요소들을 이동시켜서 빈자리를 만든 다음 삽입해야 함(시간복잡도 $O(n)$ )
삭제 => 숫자 높은 것이 우선순위가 높다고 가정할 때 맨 뒤에 위치한 요소를 삭제하면 됨(시간복잡도 $O(1)$ )

연결 리스트를 사용하는 방법

정렬이 안된 연결 리스트일 때

삽입 => 첫 번째 노드로 삽입시키는 것이 유리, 배열과 달리 다른 노드를 이동할 필요 없이 포인터만 변경하면 됨(시간복잡도 $O(1)$ )
삭제 => 포인터를 따라 모든 노드를 뒤져봐야 함(시간복잡도 $O(n)$ )

정렬된 연결 리스트일 때(우선순위가 높은 요소가 앞에 있는 것이 유리)

삽입 => 우선순위 값을 기준으로 갑입 위치를 찾아 삽입(시간복잡도 $O(n)$ )
삭제 -> 첫 번째 노드를 삭제하면 됨(시간복잡도 $O(1)$ )

힙을 사용하는 방법

힙(heap): 완전 이진 트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조, 반정렬 상태를 유지

8.3 힙

8.3.1 힙의 개념

여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조
부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말함
힙 트리는 중복된 값을 허용함에 유리(이진 탐색 트리는 중복된 값을 허용하지 않음)
힙 안의 데이터들은 느슨한 정렬 상태를 유지 -> 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
힙의 목적: 삭제 연산이 수행될 때마다 가장 큰 값을 찾아 내기만 하면 되는 것이므로(가장 큰 값은 루트노드에 있음) 전체를 정렬할 필요는 없음
힙의 종료: 최대 힙(max heap), 최소 힙(min heap)

최대 힙(max heap)
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리: key(부모 노드) >= key(자식 노드)
최소 힙(min heap)
부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리: key(부모 노드) <= key(자식 노드)

8.3.2 힙의 구현

힙은 완전 이진 트리이기 때문에 각각의 노드에 차례대로 번호를 부여할 수 있음
이 번호를 배열의 인덱스로 생각하면 배열에 힙의 노드들을 저장할 수 있음 -> 힙을 저장하는 표준적인 자료구조는 배열임
배열을 이용하여 힙을 저장하면 완전 이진 트리에서처럼 자식 노드와 부모 노드를 쉽게 알 수 있음

- 왼쪽 자식의 인덱스 = (부모 인덱스)*2
- 오른쪽 자식의 인덱스 = (부모 인덱스)*2+1

- 부모 인덱스 = (자식의 인덱스)/2

힙 구조체

#define MAX_ELEMENT 200
typedef struct{
	int key;
}element;

typedef struct{
	element heap[MAX_ELEMENT];
    int heap_size;
}HeapType;

// 힙 생성
HeapType heap1;

8.3.3 삽입 연산

새로운 노드를 힙의 마지막 노드에 이어서 삽입
그 후 힙 트리의 성질이 만족되지 않은 경우, 힙 성질을 만족할 때까지 새로운 노드와 부모 노드를 교환

<알고리즘 8.3.3.1> 힙 트리에서의 삽입 알고리즘(자연어 버전)

insert(A, key)
1. 힙의 끝에 새로운 노드를 삽입
2. 삽입된 노드와 그 부모 노드의 키 값을 비교, 삽입된 노드의 키 값이 부모 노드의 키 값보다 크면 두 노드의 위치를 바꿈
3. 삽입된 노드의 키 값이 자신의 부모 노드 키 값보다 작아질 때까지 단계 2를 반복

<알고리즘 8.3.3.2> 힙 트리에서의 삽입 알고리즘(유사코드 버전)

insert_max_heap(A, key)

heap_size <- heap_size + 1;
i <- heap_size;
A[i] <- key;

while i != 1 and A[i] > A[PARENT(i)] do
	A[i] <- A[PARENT(i)];
    i <- PARENT(i);
    
1. 힙 크기를 하나 증가
2. 증가된 힙 크기 위치에 새로운 노드를 삽입
3. i가 루트 노드가 아니고 i번째 노드가 i의 부모 노드보다 크면
4. i번째 노드와 부모 노드와 교환
5. 한 레벨 위로 올라감(승진)

<프로그램 8.3.3.1> 힙 트리에서의 삽입 함수

// 현재 요소의 개수가 heap_size인 힙 h에 item을 삽입
// 삽입 함수
void insert_max_heap(HeapType *h, element item){
	int i;
    i = ++(h->heap_size);
    
    // 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정
    // 교환이 아니고 부모노드만을 끌어 내린 다음 
    while((i != 1) && (item.key > h->heap[i/2].key){
    	h->heap[i] = h->heap[i/2];
        i/=2;
    }
    // 삽입될 위치가 확실해지면 새로운 노드는 그 위치로 이동 -> 이동 횟수를 줄일 수 있음
    h->heap[i] = item; // 새로운 노드 삽입
}

8.3.4 삭제 연산

최대 힙에서 삭제는 최대값을 가진 요소를 삭제하는 것
루트 노드가 삭제 되고, 삭제 후 힙 재구성이 필요함
힙의 재구성: 힙의 성질을 만족하기 위해 위, 아래 노드를 교환하는 것

<알고리즘 8.3.4.1> 힙 트리에서의 삭제 알고리즘

delete_max_heap(A)

item <- A[i]; // 루트 노드 값을 반환을 위해 item 변수로 옮김
A[i] <- A[heap_size]; // 말단 노드를 루트 노드로 옮김
heap_size <- heap_size-1; // 힙 크기를 하나 줄임
i <- 2; // 루트의 왼쪽 자식부터 비교 시작
while i <= heap_size do // i가 힙 트리의 크기보다 작으면(즉, 힙 트리를 벗어나지 않았으면)
	if i < heap_size and A[i+1] > A[i] // 오른쪽 자식이 더 크면
    	// 두 개의 자식 노드 중 크 값의 인덱스를 largest로 옮김
    	then largest <- i+1;
        else largest <- i;
    // largest의 부모 노드가 largest보다 크면 종료
    if A[PARENT(largest)] > A[largesr]
    	then break;
    // 그렇지 않다면 largest와 largest 부모 노드를 교환
    A[PARENT(largest)] <- A[largest];
    i <- Child(largest); // 한 레벨 밑으로 내려감
    
return item; // 최댓값을 반환

<프로그램 8.3.4.1> 힙 트리에서의 삭제 함수

// 삭제 함수
element delete_max_heap(HeapType *h){
	int parent, child;
    element item, tmp;
    
    item = h->heap[1];
    tmp = h->heap[(h->heap_size)--]; // 루트로 갈 힙 트리의 마지막 노드
    parent = 1;
    child = 2;
    
    while(child <= h->heap_size){
    	// 현재 노드의 자식 노드 중 더 큰 자식 노드를 찾는다.
        if( (child < h->heap_size) && (h->heap[child].key < h->heap[child+1].key){
        	child++;
        }
        if(tmp.key >= h->heap[child]) break;
        // 한 단계 아래로 이동
        h->heap[parent] = h->heap[child];
        parent = child; // 결과적으로 마지막 노드가 있어야 하는 위치가 됨
        child *=2;
    }
    h->heap[parent] = tmp;
    
    return item;
}

전체 프로그램

<프로그램 8.3.1> 전체 프로그램

#include <stdio.h>
#define MAX_ELEMENT 200

typedef struct{
    int key;
} element;

typedef struct {
    element heap[MAX_ELEMENT];
    int heap_size;
} HeapType;

// 초기화 함수
void init(HeapType *h){
    h->heap_size = 0;
}

void insert_max_heap(HeapType*h,element item){
    // 1. 힙 트리의 마지막 노드로 삽입
    // 2. 힙의 재구성: 최대 힙의 성질을 만족하는 트리를 만들어야 함(부모 노드 > 자식 노드)
    int i = ++(h->heap_size);
    while((i!=1)&&(h->heap[i/2].key < item.key)){
        h->heap[i] = h->heap[i / 2];
        i /= 2;
    }
    h->heap[i] = item;
}

element delete_max_heap(HeapType*h){
    // 1. 힙 트리의 루트 노드를 삭제
    // 2. 힙 트리의 마지막 노드를 루트 노드 위치로 옮김
    // 3. 힙의 재구성: 최대 힙의 성질을 만족하는 트리를 만들어야 함(부모 노드 > 자식 노드)
    element item = h->heap[1];
    element tmp = h->heap[(h->heap_size)--];
    int parent = 1, child = 2;
    while ((child <= h->heap_size)){
        if((child < h->heap_size) && (h->heap[child].key < h->heap[child+1].key )){
            child++;
        }
        if(h->heap[child].key <= tmp.key){
            break;
        }
        h->heap[parent] = h ->heap[child];
        parent = child;
        child *= 2;
    }
    h->heap[parent] = tmp;
    return item;
}

// 주 함수
int main(){
    element e1 = { 10 }, e2 = { 5 }, e3 = { 30 };
    element e4, e5, e6;
    HeapType heap; // 힙 생성
    init(&heap); // 초기화
    // 삽입
    insert_max_heap(&heap, e1);
    insert_max_heap(&heap, e2);
    insert_max_heap(&heap, e3);

    // 삭제
    e4 = delete_max_heap(&heap);
    printf("< %d > ", e4.key);
    e5 = delete_max_heap(&heap);
    printf("< %d > ", e5.key);
    e6 = delete_max_heap(&heap);
    printf("< %d >\n", e6.key);
}

프로그램 8.3.1결과

8.3.5 힙의 복잡도 분석

삽입 연산 - 새로운 요소는 힙 트리를 타고 올라가면서 부모 노드들과 교환하게 됨
최악의 경우: 루트 까지 올라가야 하므로 거의 트리의 높이에 해당하는 비교 연산 및 이동 연산이 필요함 -> 시간복잡도 $O(logn)$
삭제 연산 - 마지막 노드를 루트로 가져온 후에 자식 노드들과 비교하여 교환해야 함
최악의 경우: 가장 아래 레벨까지 내려가야 하므로 트리의 높이만큼의 시간이 걸림 -> 시간복잡도 $O(logn)$

Quiz

최대 힙이 아래와 같이 배열에 저장되어 있을 때, 11이 삽입된 후의 힙 트리?

인덱스	1	2	3	4	5	6	7	8	9
데이터	12	10	8	4	6	2	5	3

-> 11 삽입 후

인덱스	1	2	3	4	5	6	7	8	9
데이터	12	11	8	10	6	2	5	3	4

위의 최대 힙에서 우선순위가 가장 높은 요소를 삭제했을 경우에 재구성된 힙 트리?

인덱스	1	2	3	4	5	6	7	8	9
데이터	12	10	8	4	6	2	5	3

-> 12 삭제 후

인덱스	1	2	3	4	5	6	7	8	9
데이터	10	6	8	4	3	2	5

8.4 힙의 응용

힙 정렬

시간복잡도 $O(nlogn)$
1. 정렬해야 할 n개의 요소들로 최대 힙을 초기화
2. 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장 -> 삭제되는 요소들은 값이 감소되는 숨서로 정렬되게 됨

<프로그램 8.4.1> 힙 정렬 프로그램

// 우선순위 큐인 힙을 이용한 정렬
void heap_sort(element e[], int n){
	HeapType *h;
    init(&h);
    for(int i=0;i<n;i++){
    	insert_max_heap(&h, e[i]);
    }
    
    for(int i =(n-1);i>=0;i--){
    	e[i] = delete_max_heap(&h);
    }
}

이산 이벤트 시뮬레이션

컴퓨터 시뮬레이션: 실재하거나 이론적으로 존재하는 물리적인 시스템의 모델을 디자인하고 그 모델을 디지털 컴퓨터에서 실행하고 그 실형 결과를 분석하는 학문
시뮬레이션의 종류(시간에 따라 달라짐): 연속 시간(continuous time) 시뮬레이션, 이산 시간(discrete time) 시뮬레이션, 이산 이벤트(discrete event) 시뮬레이션
이산 이벤트 시뮬레이션: 모든 시간의 진행은 이벤트의 발생에 의해 이루어짐. 즉, 이벤트가 발생하면 시간이 진행되는 것임
ex) 아이스크림 가게 시뮬레이션: 아이스크림 가게에 손님들이 들어오고 나가는 과정을 시뮬레이션하는 것

손님이 도착하는 이벤트(ARRIVAL)

손님의 숫자와 현재 남아 있는 의자를 비교하여 남아 있는 의자가 저 많으면 손님을 받음
남아 있는 의자의 수는 손님의 숫자만큼 줄어듬
만약 의자가 더 적으면 손님은 주문하지 않고 나가게 됨

손님이 주문하는 이벤트(ORDER)

손님의 숫자대로 주문을 받게 됨
잠시후 손님들이 떠나는 이벤트를 발생시킴

손님이 가게를 떠나는 이벤트(LEAVE)

떠나는 손님들의 숫자만큼 남아 있는 의자들의 개수를 증가시키면 됨
-> 손님들의 숫자, 주문을 하는데 걸리는 시간, 가게에 머물러 있는 시간 등은 모두 랜덤하게 처리
-> 먼저 발생한 이벤트를 가장 먼저 처리해야 되므로 여기서 우선순위 큐는 최소 힙을 사용해야 함

<프로그램 8.4.2> 아이스크림 가게 시뮬레이션 프로그램(최소 힙 사용)

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0

#define ARRIVAL 1
#define ORDER 2
#define LEAVE 3

int free_seats = 10;
double profit = 0.0;

#define MAX_ELEMENT 100

typedef struct{
    int type; // 이벤트의 종류
    int key; // 이벤트가 일어난 시각
    int number; // 고객의 숫자
} element;

typedef struct{
    element heap[MAX_ELEMENT];
    int heap_size;
} HeapType;

// 초기화 함수
void init(HeapType *h){
    h->heap_size = 0;
}

int is_empty(HeapType *h){
    if(h->heap_size == 0){
        return TRUE;
    }else{
        return FALSE;
    }
}

// 삽입 함수
void insert_min_heap(HeapType *h, element item){
    int i = ++(h->heap_size);

    // 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정
    while((i!=1) && (h->heap[i/2].key > item.key)){
        h->heap[i] = h->heap[i / 2];
        i /= 2;
    }
    h->heap[i] = item; // 새로운 노드 삽입
}

// 삭제 함수
element delete_min_heap(HeapType *h){
    element item = h->heap[1];
    element tmp = h->heap[(h->heap_size)--];
    int parent = 1, child = 2;

    while(child <= h->heap_size){
        // 현재 노드의 자식 노드 중 더 작은 자식 노드를 찾음
        if((child < h->heap_size) && (h->heap[child].key > h->heap[child+1].key)){
            child++;
        }
        if(h->heap[child].key >= tmp.key){
            break;
        }
        // 한단계 아래로 이동
        h->heap[parent] = h->heap[child];
        parent = child;
        child *= 2;
    }
    h->heap[parent] = tmp;
    return item;
}

// 0에서 n 사이의 정수 난수 생성 함수
int random(int n){
    return (int)(n * rand() / (double)RAND_MAX);
}

// 자리가 가능하면 빈자리 수를 사람 수만큼 감소시킴
int is_seat_available(int number){
    printf("Arrival %d people\n", number);
    if(free_seats >= number){
        free_seats -= number;
        return TRUE;
    }else{
        printf("Leave because there are no seats\n");
        return FALSE;
    }
}

// 주문을 받으면 순익을 나타내는 변수를 증가시팀
void order(int scoops){
    printf("Order %d ice cream\n", scoops);
    profit += 0.35 * scoops;
}

// 고객이 떠나면 빈자리 수를 증가시킴
void leave(int number){
    printf("Leave %d people\n", number);
    free_seats += number;
}

// 이벤트를 처리함
void process_event(HeapType *h, element e){

    element new_evenet;
    printf("Current time=%d\n", e.key);
    switch(e.type){
        case ARRIVAL:
            // 자리가 가능하다면 주문 이벤트를 만듦
            if(is_seat_available(e.number)){
                new_evenet.type = ORDER;
                new_evenet.key = e.key + 1 + random(4); // 랜덤 시간 뒤에 주문 
                new_evenet.number = e.number;
                insert_min_heap(h, new_evenet);
            }
            break;
        case ORDER:
            // 사람 수만큼 주문을 받음
            for (int i = 0; i < e.number;i++){
                order(1 + random(3));
            }
            // 매장을 떠나는 이벤트를 생성
            new_evenet.type = LEAVE;
            new_evenet.key = e.key + 1 + random(10);
            new_evenet.number = e.number;
            insert_min_heap(h, new_evenet);
            break;
        case LEAVE:
            // 고객이 떠나면 빈자리 수를 증가
            leave(e.number);
            break;
    }
}

int main(){
    element event;
    HeapType heap;
    unsigned int t = 0;

    init(&heap);

    // 처음에 몇 개의 초기 이벤트를 생성
    while(t<5){
        t += random(6);
        event.type = ARRIVAL;
        event.key = t;
        event.number = 1 + random(4);
        insert_min_heap(&heap, event);
    }

    //시뮬레이션 수행
    while(!is_empty(&heap)){
        event = delete_min_heap(&heap);
        process_event(&heap, event);
    }

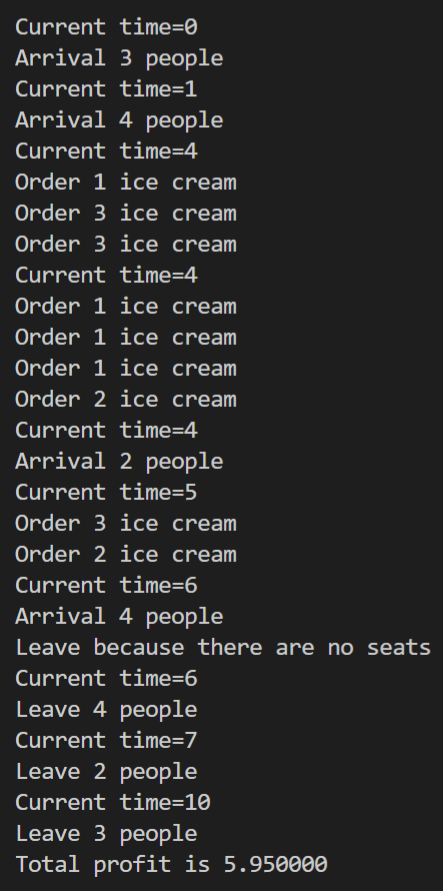
    printf("Total profit is %f\n", profit);
    return 0;
}

프로그램8.4.2결과

허프만 코드

이진 트리는 각 글자의 빈도가 알려져 있는 메시지의 내용을 압축하는데 사용될 수 있음 -> 허프만 코딩 트리
빈도수(frequencies): 각 숫자들은 영문 텍스트에서 해당 글자가 나타나는 횟수
빈도수를 이용해서 데이터를 압축할 때 각 글자들을 나타내는 최소 길이의 엔코딩 비트열을 만들 수 있음 -> 각 글자의 빈도수에 따라서 가장 많이 등장하는 글자에는 짧은 비트열을 사용하고 잘 나오지 않는 글자에는 긴 비트열을 사용하여 전체의 크기를 줄이는 것임

각각의 글자를 어떤 비트 코드로 표현했는지를 알려주는 테이블이 있을 때

글자	비트코드	빈도수	비트수
e	00	15	30
t	01	12	24
n	10	8	16
i	110	6	18
s	111	4	12
합계			88

해결해야 될 문제
1. 압축해야 할 텍스트가 주어졌을 때 어떻게 그러한 비트 코드를 자동으로 생성할 것인지
2. 압축된 텍스트가 주어져 있을 떄 어떻게 복원할 것인지
ex) teen의 경우, 가변 코드를 사용하여 코딩하면 01000010이 됨
첫 번째 글자의 경우, 하나의 글자가 4비트까지 가능하므로 0, 01, 010, 0100 중의 하나, 코드 테이블을 보면 0, 010, 0100인 코드는 없기 때문에 01이 분명함
-> 이러한 해독이 가능한 이유: 모든 코드가 다른 코드의 첫 부분이 아니기 때문, 따라서 코딩된 비트열을 왼쪽에서 오른쪽으로 조사해보면 정확히 하나의 코드만 일치하는 것을 알 수 있음 => 이러한 특수한 코드(허프만 코드(Huffman codes)를 만들기 위해서 이진 트리를 사용할 수 있음

허프만 코드가 생성되는 방법
1. 빈도수에 따라 5개의 글자를 나열(s(4), i(6), n(8), t(12), e(15))
2. 여기서 가장 작은 빈도수를 가진 글자 2개(s(4), i(6))을 추출하여 이 들을 단말 노드로 하여 이진 트리를 구성, 루트 노드의 값은 각 자식 노드의 값을 합한 값

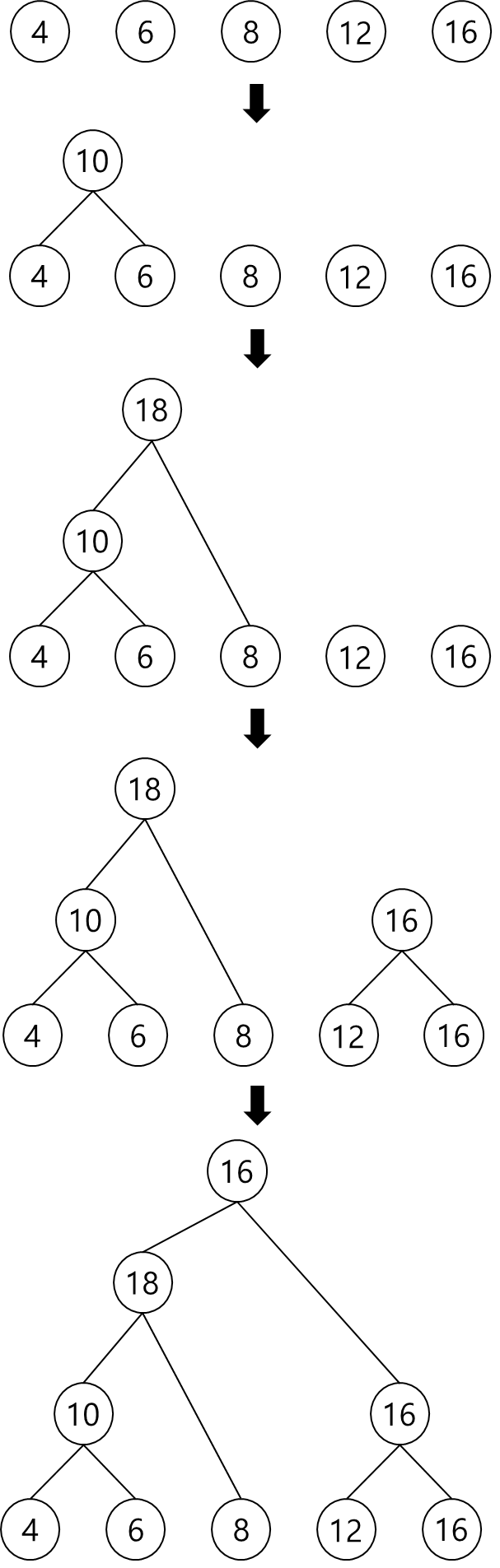
3. 위의 과정으로 이진 트리가 구성되면 왼쪽 간선은 1, 오른쪽 간선은 0 비트를 나타냄

-> 각 글자에 대한 허프만 코드는 단순히 루트 노드에서 단말 노드까지의 경로에 있는 간선의 라벨 값을 읽으면 됨
ex) 빈도수 6에 해당하는 글자인 i의 코드는 110이 됨

<프로그램 8.4.3> 허프만 코드 프로그램(최소 힙 사용)

#include <stdio.h>
#include <stdlib.h>

#define MAX_ELEMENT 100

// 우선순위는 트리의 weight 값에 의해 결정됨
typedef struct TreeNode{
    int weight;
    struct TreeNode* left;
    struct TreeNode* right;
} TreeNode;

typedef struct{
    TreeNode* ptree; // 트리를 가리키는 포인터
    int key; // 그 트리의 weight 값을 key 값으로 가짐
} element;

typedef struct{
    element heap[MAX_ELEMENT];
    int heap_size;
}HeapType;

// 초기화 함수
void init(HeapType *h){
    h->heap_size = 0;
}

// 삽입 함수
void insert_min_heap(HeapType*h,element item){
    int i = (h->heap_size)++;

    while((i!=1) && (item.key > h->heap[i/2].key)){
        h->heap[i] = h->heap[i / 2];
        i /= 2;
    }
    h->heap[i] = item;
}

// 삭제 함수
element delete_min_heap(HeapType *h){
    element item = h->heap[1];
    element tmp = h->heap[(h->heap_size)--];
    int parent = 1, child = 2;

    while(child <= h->heap_size){
        if((child < h->heap_size) && (h->heap[child].key > h->heap[child+1].key)){
            child++;
        }
        if(tmp.key <= h->heap[child].key){
            break;
        }
        h->heap[parent] = h->heap[child];
        parent = child;
        child *= 2;
    }
    h->heap[parent] = tmp;
    return item;
}

// 이진 트리 생성 함수 
// 매개변수로 받은 포인터들을 왼쪽 자식과 오른쪽 자식으로 하는 루트 노드를 만들어서 반환
TreeNode *make_tree(TreeNode*left, TreeNode *right){
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    if(node == NULL){
        fprintf(stderr, "memory allocate error\n");
        exit(1);
    }
    node->left = left;
    node->right = right;
    return node;
}

// 이진 트리 제거 함수
void destory_tree(TreeNode *root){
    if(root == NULL)
        return;
    destory_tree(root->left);
    destory_tree(root->right);
    free(root);
}

// 허프만 코드 생성 함수
void huffman_tree(int freq[], int n){
    TreeNode *node, *x;
    HeapType heap;
    element e, e1, e2;
    init(&heap);
    
    // 빈도수에 따라 각 글자들의 트리를 생성
    for (int i = 0; i < n;i++){
        node = make_tree(NULL, NULL);
        e.key = node->weight = freq[i];
        e.ptree = node;
        insert_min_heap(&heap, e);
    }

    for (int i = 1; i < n;i++){
        // 최솟값을 가지는 두 개의 노드를 삭제
        e1 = delete_min_heap(&heap);
        e2 = delete_min_heap(&heap);

        // 두 개의 노드를 합침
        x = make_tree(e1.ptree, e2.ptree);
        e.key = x->weight = e1.key + e2.key;
        e.ptree = x;
        insert_min_heap(&heap, e);
    }
    e = delete_min_heap(&heap); // 최종 트리
    destory_tree(e.ptree);
}

int main(){
    int freq[] = { 15, 12, 8, 6, 4 };
    huffman_tree(freq, sizeof(freq) / sizeof(int));
}

<참고자료>
천인국 · 공용해 · 하상호 지음,『C언어로 쉽게 풀어쓴 자료구조』, 생능출판(2016)

yj 0

이전 포스트

[책 정리] Chapter 07. 트리

다음 포스트

[책 정리] Chapter 08. 우선순위 큐

자료구조

8.1 우선순위 큐 추상 자료형

우선순위 큐의 소개

우선순위 큐의 추상 자료형

<ADT 8.1.1> 우선순위 큐

Quiz

8.2 우선순위 큐의 구현 방법

배열을 사용하는 방법

연결 리스트를 사용하는 방법

힙을 사용하는 방법

8.3 힙

8.3.1 힙의 개념

8.3.2 힙의 구현

8.3.3 삽입 연산

<알고리즘 8.3.3.1> 힙 트리에서의 삽입 알고리즘(자연어 버전)

<알고리즘 8.3.3.2> 힙 트리에서의 삽입 알고리즘(유사코드 버전)

<프로그램 8.3.3.1> 힙 트리에서의 삽입 함수

8.3.4 삭제 연산

<알고리즘 8.3.4.1> 힙 트리에서의 삭제 알고리즘

<프로그램 8.3.4.1> 힙 트리에서의 삭제 함수

전체 프로그램

<프로그램 8.3.1> 전체 프로그램

8.3.5 힙의 복잡도 분석

Quiz

8.4 힙의 응용

힙 정렬

<프로그램 8.4.1> 힙 정렬 프로그램

이산 이벤트 시뮬레이션

<프로그램 8.4.2> 아이스크림 가게 시뮬레이션 프로그램(최소 힙 사용)

허프만 코드

<프로그램 8.4.3> 허프만 코드 프로그램(최소 힙 사용)

[책 정리] Chapter 07. 트리

[책 정리] Chapter 09. 정렬

0개의 댓글