탐색 알고리즘 BFS

BFS

Breadth First Search, 너비 우선 탐색
가까운 노드부터 탐색하는 알고리즘
DFS - 최대한 멀리 있는 노드부터
수행시간이 BFS가 DFS보다 빠르다

선입선출 방식인 큐 자료구조를 이용하며, 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 된다.

동작방식
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
3. 2번의 과정을 반복

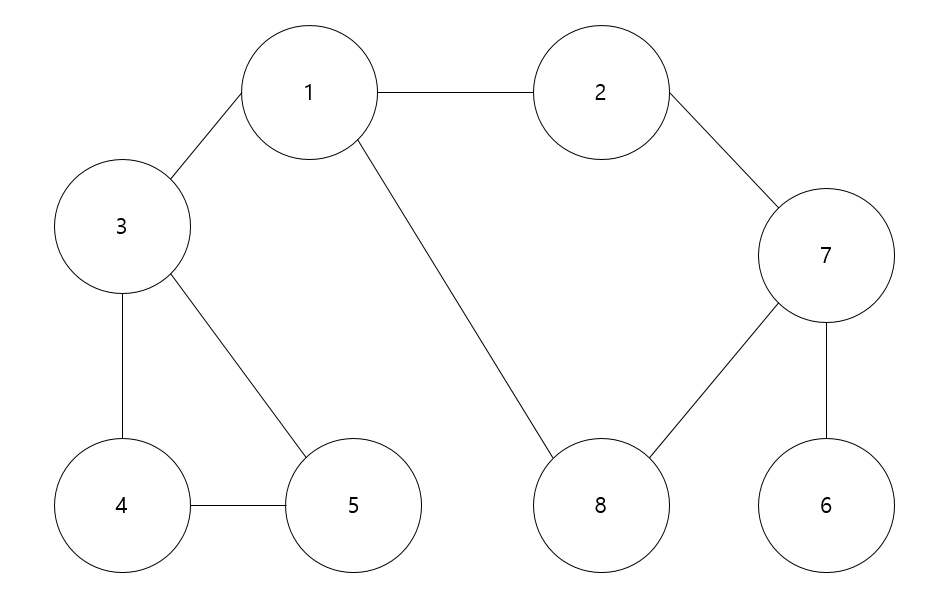
해당 그래프를 탐색해보자.

(참고: https://codingnojam.tistory.com/41)

public class StudyBFS {
	
	public static void main(String[] args) {
		
		// 그래프를 2차원 배열로 표현해줍니다.
		// 배열의 인덱스를 노드와 매칭시켜서 사용하기 위해 인덱스 0은 아무것도 저장하지 않습니다.
		// 1번인덱스는 1번노드를 뜻하고 노드의 배열의 값은 연결된 노드들입니다.
		int[][] graph = {{}, {2,3,8}, {1,7}, {1, 4, 5}, {3, 5}, {3, 4}, {7}, {2, 6, 8}, {1,7}};
		
		// 방문처리를 위한 boolean배열 선언
		boolean[] visited = new boolean[9];
		
		System.out.println(bfs(1, graph, visited));
		//출력 내용 : 1 -> 2 -> 3 -> 8 -> 7 -> 4 -> 5 -> 6 
	}
	
	static String bfs(int start, int[][] graph, boolean[] visited) {
		// 탐색 순서를 출력하기 위한 용도
        //StringBuilder 문자열 더해줌
		StringBuilder sb = new StringBuilder();
		// BFS에 사용할 큐를 생성해줍니다.
		Queue<Integer> q = new LinkedList<Integer>();
		 
		// 큐에 BFS를 시작 할 노드 번호를 넣어줍니다.
		q.offer(start);
		
		// 시작노드 방문처리
		visited[start] = true;
		
		// 큐가 빌 때까지 반복
		while(!q.isEmpty()) {
			int nodeIndex = q.poll();
			sb.append(nodeIndex + " -> ");
			//큐에서 꺼낸 노드와 연결된 노드들 체크
			for(int i=0; i<graph[nodeIndex].length; i++) {
				int temp = graph[nodeIndex][i];
				// 방문하지 않았으면 방문처리 후 큐에 넣기
				if(!visited[temp]) {
					visited[temp] = true;
					q.offer(temp);
				}
			}
		}
		// 탐색순서 리턴
		return sb.toString() ;
	}
}

---

BFS 실전 문제

미로탈출

동빈이는 N x M 크기의 직사각형 형태의 미로에 갇혀 있다. 미로에는 여러 마리의 괴물이 있어 이를 피해 탈출해야 한다. 동빈이의 위치는 (1,1)이고 미로의 출구는 (N, M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있다. 이때 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있다. 미로는 반드시 탈출할 수 있는 형태로 제시된다. 이때 동빈이가 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하시오. 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산한다.

입력 조건
--첫째 줄에 두 정수 N,M(4 <= N, M <= 200)이 주어집니다. 다음 N개의 줄에는 각각 M개의 정수(0 혹은 1)로 미로의 정보가 주어진다. 각각의 수들은 공백 없이 붙어서 입력으로 제시된다. 또한 시작 칸과 마지막 칸은 항상 1 이다.
출력 조건
-- 첫째 줄에 최소 이동 칸의 개수를 출력한다.

---

풀이

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class 미로찾기 {
	//상하좌우
	static int[] dx = {-1, 1, 0, 0};
	static int[] dy = {0, 0, -1, 1};

	static int n, m;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		
		n = sc.nextInt();
		m = sc.nextInt();
		int[][] graph = new int[n][m];
		
		for(int i = 0; i < n; i++) {
			String number = sc.next();
			for(int j = 0; j < m; j++) {
				graph[i][j] = Integer.parseInt(String.valueOf(number.charAt(j)));
			}
		}
		
		System.out.println(bfs(0,0, graph));
		
	}
	
	public static int bfs(int x, int y, int[][] graph) {
		int nx = 0, ny = 0;
		Integer[] v = {x, y};
		Queue<Integer[]> q = new LinkedList<Integer[]>();
		q.offer(v);
		while(!q.isEmpty()) {
 			//선입선출
			Integer[] index = q.poll();
			x = index[0];
			y = index[1];
			
			
			for(int i = 0; i < 4; i++) {
				nx = x + dx[i];
				ny = y + dy[i];
				
				if(nx < 0 || ny < 0 || nx > n-1 || ny > m-1 || (nx == 0 && ny == 0)) {
//				범위를 벗어나는 경우
					continue;
				}else if(graph[nx][ny] == 0) {
//					몬스터
					continue;
				}else if(graph[nx][ny] == 1) {
//					갈수있는 길
					//방문처리, 노드의 값을 변경시킴 --> 방문할 수록 값이 오르므로 이는 곧 지나간 노드의 수가됨
					graph[nx][ny] = graph[x][y] + 1;
					Integer[] n = {nx, ny};
					//큐에 추가
					q.offer(n);
				}
			}
		}
		//배열의 가장 마지막(출구)의 값이 이동한 거리가 됨
		return graph[n-1][m-1];
	}
}