KMP 알고리즘 (문자열 매칭)

KMP 알고리즘

대표적인 문자열 매칭 알고리즘이다. 문자열 매칭이란 특정한 글이 있을 때 그 글 안에서 하나의 문자열(= 여기서는 패턴이라고 부르겠다)을 찾아내는 것을 의미한다. 쉽게 말하면 우리가 브라우저에서 ctrl+f를 통해 찾고자하는 문자열을 검색하는 행위라고 생각하면 된다. 일단 kmp 알고리즘을 다루기 전에, 단순한 브루트 포스 방식으로 접근해보자.

말그대로 텍스트 인덱스를 하나씩 움직이면서, 패턴 길이만큼 떼어낸 부분 문자열을 비교하여 패턴과 동일한 지 비교하는 방식이다.

예를 들어 텍스트는 ABABABCAABABABC, 패턴은 ABABC가 입력되었다고 가정했을때,
ABABA (인덱스 0에서 시작, 패턴 매칭X)
BABAB (인덱스 1에서 시작, 패턴 매칭X)
ABABC (인덱스 2에서 시작, 패턴 매칭O)
....
이런식으로 텍스트의 마지막 글자에 도달할 때까지 모든 경우의 수를 비교하게 될 것이다.

이렇게 단순하게 모든 경우를 다 비교하는 경우는 최악의 경우 엄청난 시간이 소요될 수 있는데, 예를 들어 길이가 10,000,000인 텍스트에서 길이가 1,000인 패턴을 찾는 다면 1억번 이상의 연산을 수행해야한다. 따라서 모든 경우를 비교하지 않아도 패턴을 찾아낼 수 있는 kmp 알고리즘을 사용할 수 있어야 한다. 아래 글을 통해 단계별로 kmp 알고리즘의 핵심을 짚어보자.

1. 패턴 내 접두사 접미사 개념을 활용하자

kmp 알고리즘의 핵심은 패턴의 접두사와 접미사 개념을 적극 활용하여 '반복되는 연산을 얼만큼 건너뛸 수 있는 지'에 대해 집중한다는 것이다.
패턴 내에 존재하는 접두사와 접미사가 '일치' 한다면 접미사를 접두사로 다시 바라봄으로써 문자열 탐색을 이어서 진행할 수 있기 때문이다.

아마 글로는 단 번에 이해되지 않을 것이다. 아래 그림과 같이 '별똥같은별똥같은별똥별' 이란 텍스트에에서 '별똥같은별똥별' 패턴을 찾아야한다고 가정해보자.

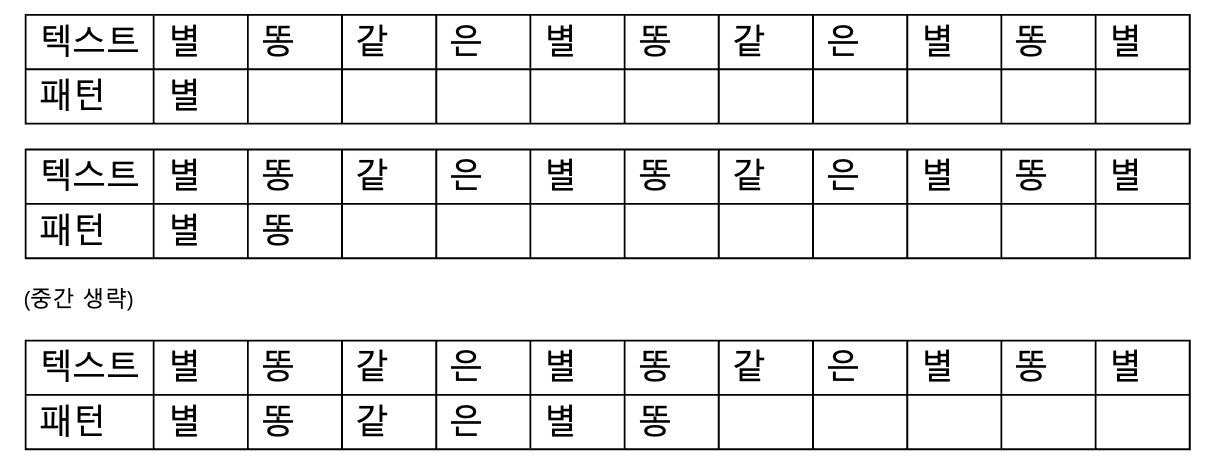
처음엔 위 그림과 같이 텍스트와 패턴 인덱스 모두 0부터 시작해서, 패턴과의 일치여부를 반복하여 확인할 것이다.

그러다가 위와 같이 텍스트와 패턴의 불일치가 일어나 매칭에 실패 하는 경우가 발생할 수 있다.
그렇다면 그 다음 값인 '똥(인덱스 1)~' 부터 확인해봐야할까?

우리는 앞서 패턴의 접미사 접두사를 적극 활용 하기로 하였다.
지금까지 확인된 텍스트에서(별똥같은별똥같), 패턴 내 접두사와 접미사가 일치하면서 그 길이가 최대인 부분을 찾아보자. 해당 부분은 별똥 이다.

접두사와 접미사가 일치한다면 접미사를 접두사로 다시 바라볼 수 있다 고 하였으므로 현재 접미사로 보고 있는 별똥 부분을, 다시 탐색할 때에는 접두사로 바라보고 해당 부분부터 다시 시작하는 것이다. 이렇게 하게되면 단순히 모든 문자를 탐색하는 것보다 따르게 패턴을 찾아낼 수 있다.

이제 아까 이해가 잘 되지 않았던 글 문단 을 빠르게 다시 읽고 와보자. 아마 이해가 훨씬 수월할 것이다.

2. 동일 접두사-접미사 전처리 테이블을 만들자

1을 통해 kmp 알고리즘에서 패턴 내 접두사와 접미사 개념을 활용하는 법에 대해 그림을 통해 배워보았다. 그렇다면 이를 어떤 식으로 알고리즘화하여 구현할 수 있을까?

먼저 생각해야할 점은, 패턴 안에서 접두사와 접미사가 일치하는 경우는 패턴에 따라 여러개가 만들어질 수 있다는 것이다. 위의 예시에선 패턴에서 찾을 수 있는 동일한 접두사-접미사가 '별똥' 밖에 존재하지 않아 적합한 예시가 되지 못하으로 아래의 다른 예시를 통해 확인해보자.

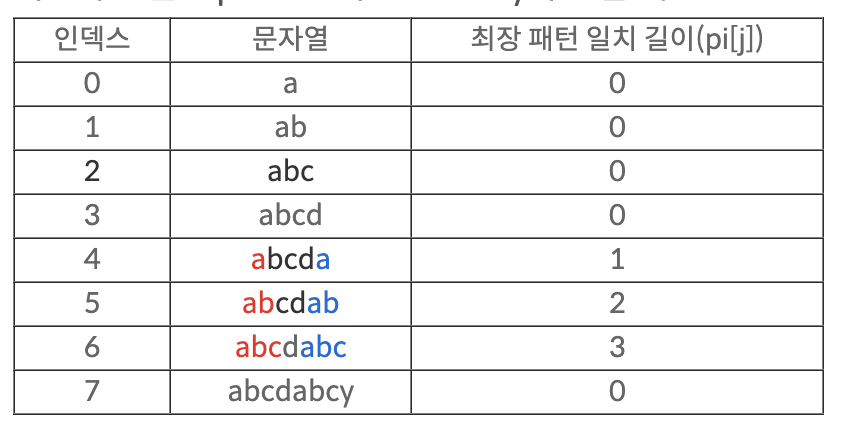
위 그림은 abcdabcy라는 패턴이 입력으로 주어졌을 때 만들어질 수 있는 동일 접두사-접미사 테이블을 나타낸 것이다. 패턴 내에서 글자를 하나씩 늘려가면서 접두사와 접미사가 일치하는 경우를 미리 확인하는 과정이라고 생각하면 된다.

여기서 고려해야할 점은 단순히 어떤 동일 접두사-접미사가 있는지만 확인하는 것이 아니라, 해당 접두사-접미사가 일치하는 최대 길이 값을 저장해야한다는 것이다. 우리가 그림을 통해서는 문자열 탐색을 다시 시작하는 지점을 직관적으로 알 수 있었지만, 실제 코드에서는 최대 일치 길이 값을 알아야만 그 값을 기준으로 인덱스를 점프하여 연산을 건너뛸 수 있기 때문이다.

코드 구현

위에서 얘기한 것들을 Python으로 구현하면 아래와 같다.

# KMP 알고리즘을 수행하기 전, 패턴을 처리하는 함수
# 테이블 생성 함수
def KMP_table(pattern):
    lp = len(pattern)
    tb = [0 for _ in range(lp)] # 테이블 리스트
    
    pidx = 0 # 테이블 값을 불러오거나 갱신 & 패턴의 인덱스 접근(접두사)
    for idx in range(1, lp): # 패턴의 인덱스 접근(접미사)
        # pidx가 0이 되거나, pidx번째 글자와 idx번째 글자가 같아질때까지 진행
        while pidx > 0 and pattern[pidx] != pattern[idx]:
            pidx = tb[pidx-1]
        
        # 값이 일치하는 경우, pidx 1 증가시키고 그 값을 tb에 저장
        if pattern[idx] == pattern[pidx] :
            pidx += 1
            tb[idx] = pidx
    
    return tb

pidx 는 접두사 포인터(and 패턴 일치 길이값을 갱신하기 위한 변수), idx 는 접미사 포인터라고 생각하고 하나씩 접미사와 접두사를 늘려가면서 비교한다고 생각하면 쉽다.

• 만약 pidx번째 글자와 idx 글자가 같다면, 패턴 일치 길이가 1칸 늘어난 것이므로 pidx를 1 증가시키고 그 값을 접두사-접미사 테이블의 idx번째에 저장한다.
• pidx번째 글자와 idx 글자가 같지 않다면, 현재 문자열에선 동일 접두사-접미사가 존재하지 않다는 뜻이므로 접두사 포인터인 pidx는 이전으로(=동일 접두사-접미사가 존재했던 문자열) 되돌아간다으로 되돌아간다. 이는 pidx-1번째 테이블 값을 pidx에 갱신해줌으로써 구현할 수 있다.

결국 다시 정리하면, 하나씩 접미사와 접두사를 늘려가면서 비교하다가 일치하지 않는 경우가 생기면 일치했었던 부분까지 되돌아가서 다시 검사를 하는 방식으로 테이블을 구축하는 것이다.

3.KMP 함수를 만들자.

이제 2번에서 만든 동일 접두사-접미사 전처리 테이블을 바탕으로 문자열 탐색 과정을 끝까지 진행해보자. 테이블 함수를 만드는 로직과 매우 비슷하기 때문에 위에서 잘 이해했다면 빠르게 이해할 수 있을 것이다. 참고로 아래 KMP 함수는 해당 패턴이 몇 번 나타나는 지, 그 때의 시작 인덱스가 몇인지를 리턴한다.

def KMP(word, pattern):
    # KMP_table 통해 전처리된 테이블 불러오기
    table = KMP_table(pattern)
    
    results = [] # 결과를 만족하는 인덱스 시점을 기록하는 리스트
    pidx = 0
    
    for idx in range(len(word)):
        # 단어와 패턴이 일치하지 않는 경우, pidx를 table을 활용해 값 변경
        while pidx > 0 and word[idx] != pattern[pidx] :
            pidx = table[pidx-1]
        # 해당 인덱스에서 값이 일치한다면, pidx를 1 증가시킴
        # 만약 pidx가 패턴의 끝까지 도달하였다면, 시작 인덱스 값을 계산하여 추가 후 pidx 값 table의 인덱스에 접근하여 변경
        if word[idx] == pattern[pidx]:
            if pidx == len(pattern)-1 :
                results.append(idx-len(pattern)+1)
                pidx = table[pidx]
            else:
                pidx += 1
    
    return results

전체 코드

# KMP 알고리즘을 수행하기 전, 패턴을 처리하는 함수
# 패턴의 테이블 생성
def KMP_table(pattern):
    lp = len(pattern)
    tb = [0 for _ in range(lp)] # 정보 저장용 테이블
    
    pidx = 0 # 테이블의 값을 불러오고, 패턴의 인덱스에 접근
    for idx in range(1, lp): # 테이블에 값 저장하기 위해 활용하는 인덱스
        # pidx가 0이 되거나, idx와 pidx의 pattern 접근 값이 같아질때까지 진행
        while pidx > 0 and pattern[idx] != pattern[pidx]:
            pidx = tb[pidx-1]
        
        # 값이 일치하는 경우, pidx 1 증가시키고 그 값을 tb에 저장
        if pattern[idx] == pattern[pidx] :
            pidx += 1
            tb[idx] = pidx
    
    return tb
    
    
def KMP(word, pattern):
    # KMP_table 통해 전처리된 테이블 불러오기
    table = KMP_table(pattern)
    
    results = [] # 결과를 만족하는 인덱스 시점을 기록하는 리스트
    pidx = 0
    
    for idx in range(len(word)):
        # 단어와 패턴이 일치하지 않는 경우, pidx를 table을 활용해 값 변경
        while pidx > 0 and word[idx] != pattern[pidx] :
            pidx = table[pidx-1]
        # 해당 인덱스에서 값이 일치한다면, pidx를 1 증가시킴
        # 만약 pidx가 패턴의 끝까지 도달하였다면, 시작 인덱스 값을 계산하여 추가 후 pidx 값 table의 인덱스에 접근하여 변경
        if word[idx] == pattern[pidx]:
            if pidx == len(pattern)-1 :
                results.append(idx-len(pattern)+2)
                pidx = table[pidx]
            else:
                pidx += 1
    
    return results

🦾 깨달은 점

여러 개발 포스팅과 영상을 보고 내재화 (내 언어로 풀어 설명하되 깔끔하고 남이 보기에 한 눈에 이해할 수 있도록 작성하기. 부족하다면 직접 도식화해보기) 하는 과정을 거쳐야만 온전히 알고리즘을 이해할 수 있는 것 같다 💬 ⚖️ 시간은 꽤 걸리더라도 들인만큼 기억에 오래남는다는 것을 잊지 말자 👟

참고 및 추천 포스팅