위상정렬
사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열 하는 것을 의미한다.
예를 들어 아래와 같이 선수과목을 고려해 수강신청을 해야한다고 했을 때,
 세 과목을 모두 듣기 위한 적절한 학습 순서는 자료구조 -> 알고리즘 -> 고급 알고리즘이 될것이다. 만약 자료구조를 수강한 뒤 고급 알고리즘을 먼저 듣게 되면, 이후 알고리즘을 신청할 때 방향성에 거르스게 되므로, 이는 적절치 못한 학습 순서가 된다.
세 과목을 모두 듣기 위한 적절한 학습 순서는 자료구조 -> 알고리즘 -> 고급 알고리즘이 될것이다. 만약 자료구조를 수강한 뒤 고급 알고리즘을 먼저 듣게 되면, 이후 알고리즘을 신청할 때 방향성에 거르스게 되므로, 이는 적절치 못한 학습 순서가 된다.
또한 사이클이 있다면 시작 지점을 특정할 수가 없으므로 위상정렬은 꼭 사이클이 없는 방향 그래프(Direct Acyclic Graph)에서만 적용 가능하다.
진입차수와 진출차수
위상정렬을 구현하기 위해서는 그래프에서 자주 나오는 개념인 진입차수와 진출차수를 알아야한다.
- 진입차수 (indegree) : 특정 노드로 들어오는 간선의 개수
- 진출차수 (outdegree) : 특정 노드로 나가는 간선의 개수
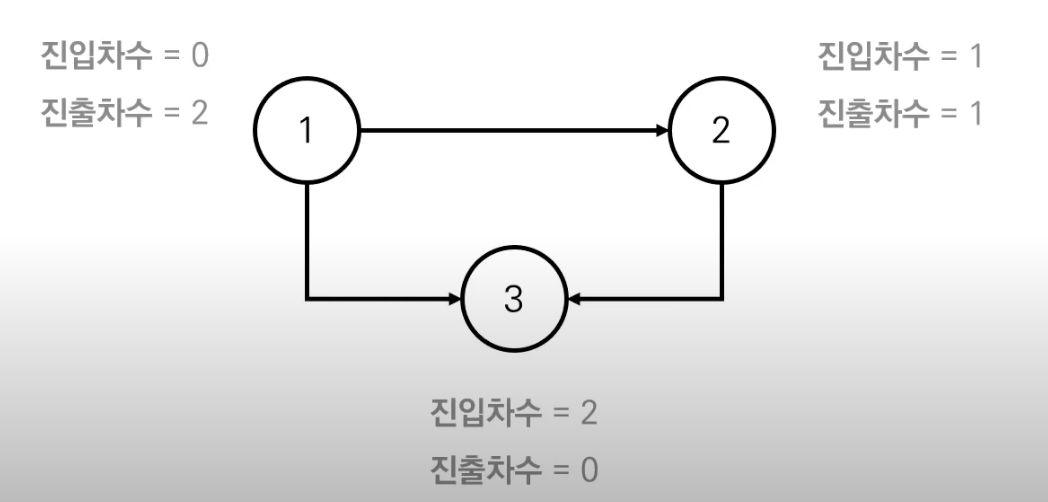
그림만 보아도 단번에 이해되니 별도의 설명은 하지 않겠다. 참고로 위상정렬은 진출차수는 상관하지 않고 진입차수만 고려하여도 충분히 구현해낼 수 있다.
동작과정
위상정렬 알고리즘은 큐를 이용한다.
- 진입차수가 0인 모든 노드를 큐에 넣는다.
- 큐가 빌 때까지 아래 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
결과적으로 큐에 들어온 노드들의 순서가 곧 위상 정렬을 수행한 결과 가 된다.
동작 예시는 해당 영상을 참고하면 도움이 될 것이니 꼭 한 번 시청하길 바란다 👍🏻
위상정렬의 특징
-
앞서 말했듯 위상정렬은 DAG에서만 수행이 가능하다.
- DAG(direct acyclic graph) : 순환하지 않는 방향 그래프
- 사이클이 있다면 진입차수가 0인 노드가 없게 되므로 사이클에 포함된 원소 중에서 어떠한 원소도 큐에 들어갈 수 없다. 따라서 모든 원소를 방문하기 전에 큐가 비게 된다면 사이클이 존재한다는 뜻이고, 결국 이는 dag가 아니기 때문에 위상 정렬을 수행할 수 없다.
-
위상정렬에서는 여러가지 답이 존재할 수 있다.
- 한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우가 있다면 여러 가지 답이 존재할 수 있다. 이런 상황에서는 보통 숫자가 작은 원소를 먼저 꺼내는 경우가 많으나 그렇지 않아도 상관없다는 뜻이다. 어짜피 전체 정렬 결과에 있어 오류가 존재할 일은 없기 때문이다.
-
스택을 활용한 DFS를 이용해 위상 정렬을 수행할 수도 있다.
코드 구현
from collections import deque
v, e = map(int, input().strip().split())
indegree = [0] * (v + 1)
graph = [[] for i in range(v + 1)]
for _ in range(e):
a, b = map(int, input().strip().split())
graph[a].append(b)
indegree[b] += 1
def topological_sort():
result = []
q = deque()
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
while q:
now = q.popleft()
result.append(now)
for i in graph[now]:
indegree[i] -= 1
if indegree[i] == 0:
q.append(i)
for i in result:
print(i, end=" ")
topological_sort()
