Knapsack 알고리즘
배낭에 담을 수 있는 무게의 최댓값이 정해져 있고, 일정한 가치의 무게가 정해진 짐들을 배낭에 담을 때, 가치의 합이 최대가 되는 조합을 찾는 알고리즘이다.
-
Fractional Knapsack Problem
말 그대로 물건을 쪼갤 수 있는 배낭 문제이다. 가치가 높은 순으로 정렬한 뒤 배낭에 담고, 텍스트남은 부분은 물건을 쪼개어 넣어 조합을 찾을 수 있을 수 있다. 그리디 알고리즘으로 해결 가능 -
Knapsack Problem
물건을 쪼갤 수 없는 배낭 문제로, 동적계획법(Dynamic Programming)을 활용해 해결 가능하다
Fractional Kanpsack Problem
앞서 말한 것 처럼 가치가 높은 순으로 짐들을 정렬하고 그리디하게 풀어나가면 된다. 이 때 어떤 것을 기준으로 잡느냐에 따라 수행방식이 달라질 수 있다.이는 문제에 따라 다르다.
보통 Fractional Knapsack 문제의 경우 무게 당 이익(= 이익 // 무게 )이 큰 것을 기준으로 잡고, 차례대로 물건을 담는다.
담다보면 가방의 용량을 넘어서는 경우가 있는데, 이 때는 가방의 남은 용량만큼만 짐을 넣는다. 여기서 하나의 짐을 온전히 넣지 못하고 짐을 쪼개야하는 상황이 발생하기 때문에 Fractional Knapsack Problem 으로 정의된다.
코드
cargo = [
(4, 12),
(2, 1),
(10, 4),
(1, 1),
(2, 2),
]
def fractional_knapsack(cargo):
capacity = 15
pack = []
# 단가 계산 역순 정렬
for c in cargo:
pack.append((c[0] / c[1], c[0], c[1]))
pack.sort(reverse=True)
# 단가 순 그리디계산
total_value: float = 0
for p in pack:
if capacity - p[2] >= 0:
capacity -= p[2]
total_value += p[1]
else:
fraction = capacity / p[2]
total_value += p[1] * fraction
break
return total_value
r = fractional_knapsack(cargo)
print(r)위 코드의 경우 단가를 기준으로 리스트를 내림차순 정렬하였으며, 짐이 용량을 넘어서는 시점에 해당 짐을 fraction으로 쪼개서 답을 구하고 있음을 알 수 있다. 이를 기준 코드로 삼아서 다양한 fractional knapsack 문제를 풀이할 수 있을 것이다.
Kanpsack Problem
알고리즘 과정
가방에 담을 물건 1~4의 무게와 가치 정보는 아래 표와 같고, 가방에 넣을 수 있는 최대 무게가 7kg라고 하였을 때 최대의 가치를 갖는 물건의 조합을 구해보자.

먼저 2차원 dp 배열을 만들어준다.
여기서 행은 물건의 번호를 의미하고, 열은 가방에 넣은 무게를 의미한다.
물건 1을 넣었을 때 갖는 최대 가치
물건 2까지 넣었을 때 갖는 최대 가치
물건 3까지 넣었을 때 갖는 최대 가치
를 계속 나아가다 보면 물건 N까지 넣었을 때 갖는 최대 가치를 찾을 수 있다.
물건 1을 넣었을 때

물건 1은 6kg이므로 당연히 6kg 이후부터 가치가 매겨질 것이다.
따라서 6kg, 7kg 열에 물건 1의 가치인 13을 입력한다.
(가능한 무게가 7kg여도 6kg와 동일하게 13임)
물건 2까지 넣었을 때
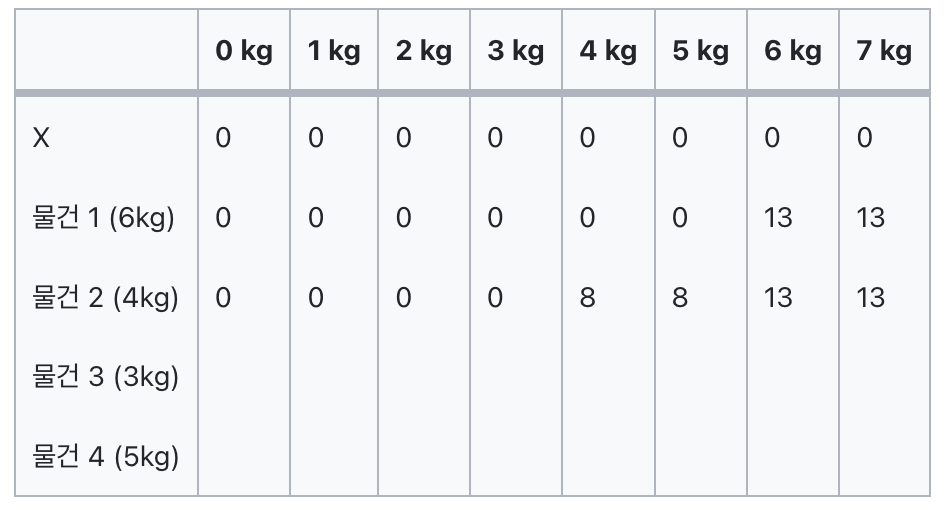
물건 2는 4kg이므로 4kg부터 가치가 매겨진다.
따라서 최대 가능 무게가 4,5kg의 경우 물건2의 가치인 8을 적고
6,7kg의 경우 물건2보다 물건1의 가치가 여전히 더 크기 때문에 그대로 둔다.
물건 3까지 넣었을 때
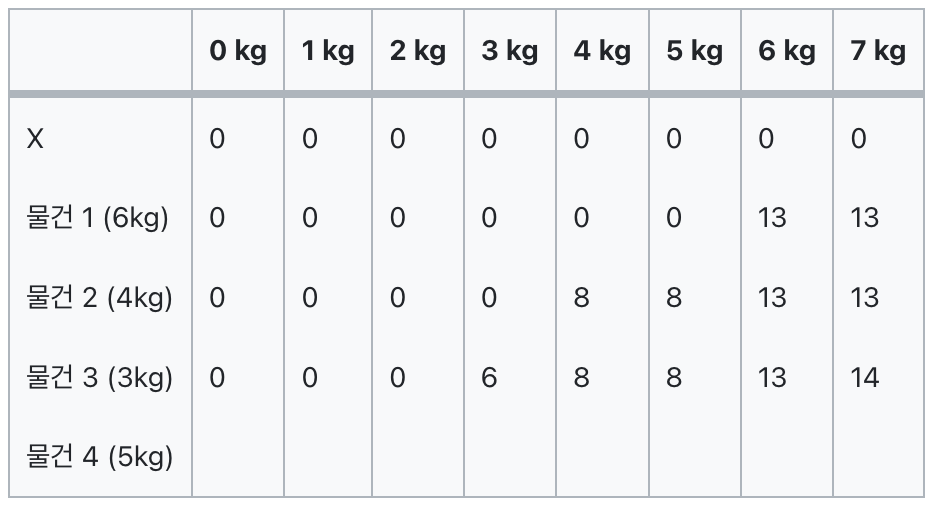
여기서부터가 좀 중요한데 (점화식을 도출해낼 수 있는 부분이기 때문에)
일단 물건 3은 3kg이므로 3kg부터 가치가 매겨진다.
따라서 최대 가능 무게가 3kg의 경우 물건 3의 가치인 3을 적는다.
3~6kg의 경우 이전 물건의 가치가 현재 물건의 가치보다 더 크기 때문에 그대로 둔다.
그러나 7kg의 경우 현재 가치인 무게1의 가치(13)보다 물건2(8)+현재 물건의 가치(6)=14 가 더 크기 때문에 14로 업데이트 해준다.
정리하면, 현재 물건까지 고려했을 때의 최대 가치는
현재 열에서 현재 물건의 무게를 뺀 열의 가치 + 현재 물건의 가치 와
현재 가치 중에서 더 큰 값으로 갱신해주면 되는것이다.
점화식
dp[i][j]=max(dp[i−1][j],dp[i−1][j−w]+v)
v = 현재 물건의 가치
w = 현재 물건의 무게를 의미한다
i = 현재 물건의 순서 번호
j = 최대 가능 무게
코드
import sys
input = sys.stdin.readline
n, k = map(int, input().strip().split())
size = [0]
value = [0]
for _ in range(n):
s, v = map(int, input().strip().split())
size.append(s)
value.append(v)
dp = [[0] * (k + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
s = size[i]
v = value[i]
for j in range(i, k + 1):
if j < s:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - s] + v)
print(dp[n][k])
또한 해당 백준 문제는 배낭 알고리즘을 그대로 구현해내는 기본 문제이기 때문에 워밍업으로 한 번 풀이해봐도 좋을 것 같다.
사실 배낭 알고리즘은 정말 특별한 것이 없다. 다른 dp들과 똑같이 dp 테이블을 업데이트하는 사이클을 돌면서 점화식을 찾아내는 것 뿐이다 !
