문제
풀이
백트래킹인가 고민하다 잘 모르겠어서 결국 다른 풀이를 참고해서 풀었다.
전형적인 dp 문제였다 (ㅋㅋ) 시간제한도 0.5초이기 때문에 매우 빨리 풀어내야 한다.
dp는 1) 문제를 작게 나눠서 보고, 이후 2) 점화식을 찾으면 된다.
1) 문제에서 '가치의 합이 k원이 되는 경우의 수'를 구하라는 문장을
'가치의 합이 i(0<=i<=k)원이 되는 경우의 수'로 작게 나눠 볼 수 있다.
(여기서 먼저 dp 테이블의 형태가 [0]*(k+1) 일 것이라고 유추해 볼 수 있음)
2) 이제 가치의 합이 i가 되는 경우의 수를 구하는 점화식을 찾아보자.
바로 떠올리긴 힘드니, 예제를 통해 생각해보자.
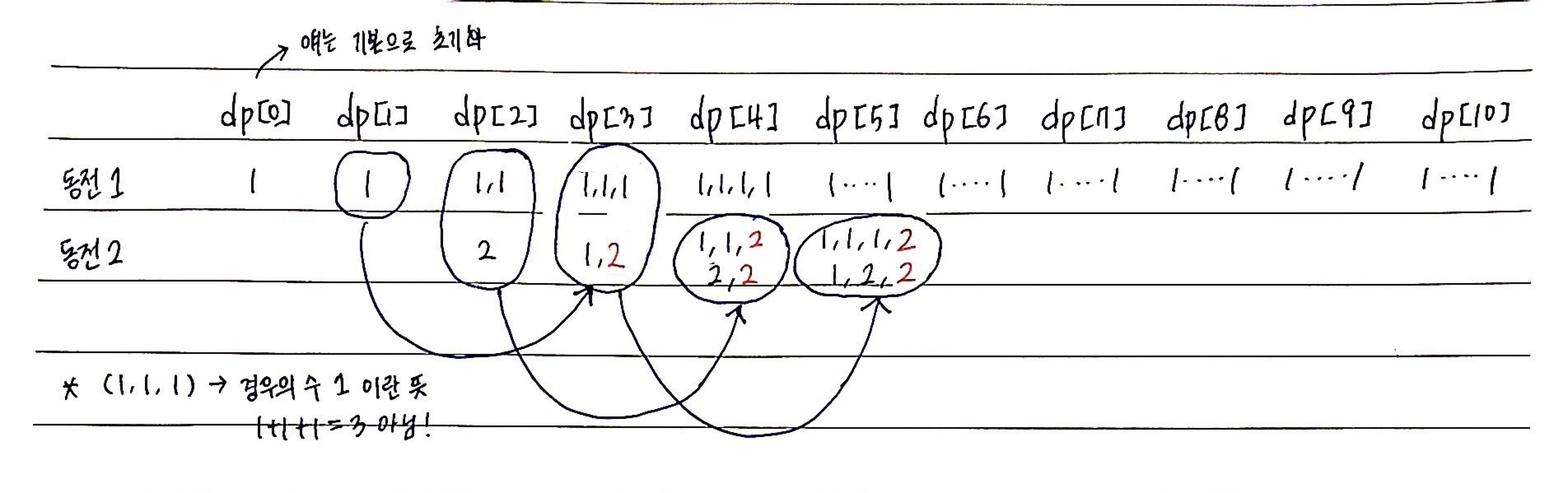
예제에서 동전의 구성이 1, 2, 5일 때 가치의 합이 10이 되는 경우의 수를 찾아야한다.
먼저 동전 1을 통해 1원~10원까지 만드는 경우의 수는 모두 1이다. dp[1]~dp[10] 모두 1로 갱신된다.
그 다음 동전 2가 추가되었다고 생각해보자.
1원을 만들어보자. 2원짜리 동전을 가지고 2원보다 작은 값을 만들 수 있을까? 불가하다. 그러니 1원을 만드는 경우의 수는 기존 그대로 1이다. 다시 말하면 dp[1]은 갱신되지 않는다. 즉, 현재 동전의 가치보다 작은 값들은 더이상 갱신되지 않으므로 이들은 dp값이 확정되었다고 볼 수 있다
2원을 만드는 경우의 수는 어떻게 될까? 기존에 1원으로만 만들었던 경우의 수 (1+1)에서 새로 추가된 동전을 사용하게 되는 경우(2)가 추가되므로 경우의 수는 총 2이다. dp[2]=2로 갱신된다.
다음 3원을 만드는 경우도 생각해보자. 기존에 1원으로만 만들었던 경우의 수 (1+1+1)에서 새로 추가된 동전 2를 사용하게 되는 경우(1+2)가 추가되므로 경우의 수는 총 2이다. dp[3]=2로 갱신된다.
여기서 새로 추가된 동전을 사용하게 되는 경우(1+2)를 뜯어보자.
왜라고 묻는다면.. 어떻게든 점화식을 찾아내기 위함이다 ✍ (´ι _` )
(1+2)은 1원을 만들수 있는 경우의 수(1)에서 2라는 값을 추가해 준 행위이다. 여기서 우리는 ⭐️ 기존의 경우의 수에 값을 추가한다고 해서 경우의 수가 바뀌지 않는다는 점을 알아야한다. 즉, dp[3] = dp[1]이다. 정확히 말하면 기존 값에서 갱신을 해야하는 것이므로 dp[3] = (기존) dp[3] + dp[1] 가 될 것이다.
아직 이해가 되지 않는다면 4원을 만드는 경우의 수도 생각해보자. 기존에 1원으로만 만들었던 경우의 수 (1+1+1+1)에서 새로 추가된 동전 2를 사용하게 되는 경우 (1+1+2), (2+2)가 추가되므로 경우의 수는 총 3이다. 아까와 같이 뜯어서 해석해보자. (1+1+2)와 (2+2)는 2원을 만들 수 있는 경우의 수(1+1),(2)에서 2라는 값을 추가해 준 행위이다. 아까와 마찬가지로 기존의 경우의 수에 값을 추가한다고 해서 경우의 수가 바뀌지 않는다. 따라서 dp[4]=dp[2]이며, 기존 것을 포함하면 dp[4] = (기존) dp[4] + dp[2]이다.
결국 이를 최종 점화식으로 표현하면,
dp[i] = dp[i] + dp[i - coin]
이다. 아직도 왜 dp[i-coin] 값을 더하는 지 이해가 가지 않는 다면 필자처럼 직접 그려가면서 생각해봐도 좋을듯 하다.
n, k = map(int, input().strip().split())
arr = []
for _ in range(n):
arr.append(int(input()))
dp = [0 for i in range(k + 1)]
dp[0] = 1
for coin in arr:
for i in range(coin, k + 1): # 현재 갖고 있는 동전 coin를 기준으로 coin 미만의 값은 갱신될리 없으므로 i부터 시작.
dp[i] += dp[i - coin]
print(dp[k])
다시 말하지만 dp는 무조건 점화식이다. 점화식만 잘 찾아내면 정답 찾기는 쉽다. 예외상황에 몰두 하기보다는 점화식을 찾기 위해 여러 상황을 반복해서 그려보고, 또 적어 내려가 보는 것이 dp 풀이에 큰 도움이 될 것 같다.
