문제
풀이
직전에 2293번 동전1 문제를 풀었기 때문에 매우 순조롭게 풀이할 수 있었다. 해당 문제도 전형적인 dp 문제이다.
dp 풀이 순서대로 1) 문제를 작게 나눠서 보고, 이후 2) 점화식을 찾아보자.
1) 문제에서 '가치의 합이 k원이 되는 동전 최소 개수'를 구하라는 문장을
'가치의 합이 i(0<=i<=k)원이 되는 동전 최소 개수'로 작게 나눠 볼 수 있다.
(여기서 우리는 dp 테이블의 형태가 [0]*(k+1) 일 것이라고 유추해 볼 수 있음)
2) 이제 가치의 합이 i가 되는 동전 최소 개수를 구하는 점화식을 찾아보자.
이번에도 예제를 보며 생각해보자.
예제에서 동전의 구성이 1, 5, 10일 때 가치의 합이 15가 되는 동전 최소 개수를 찾아야한다.
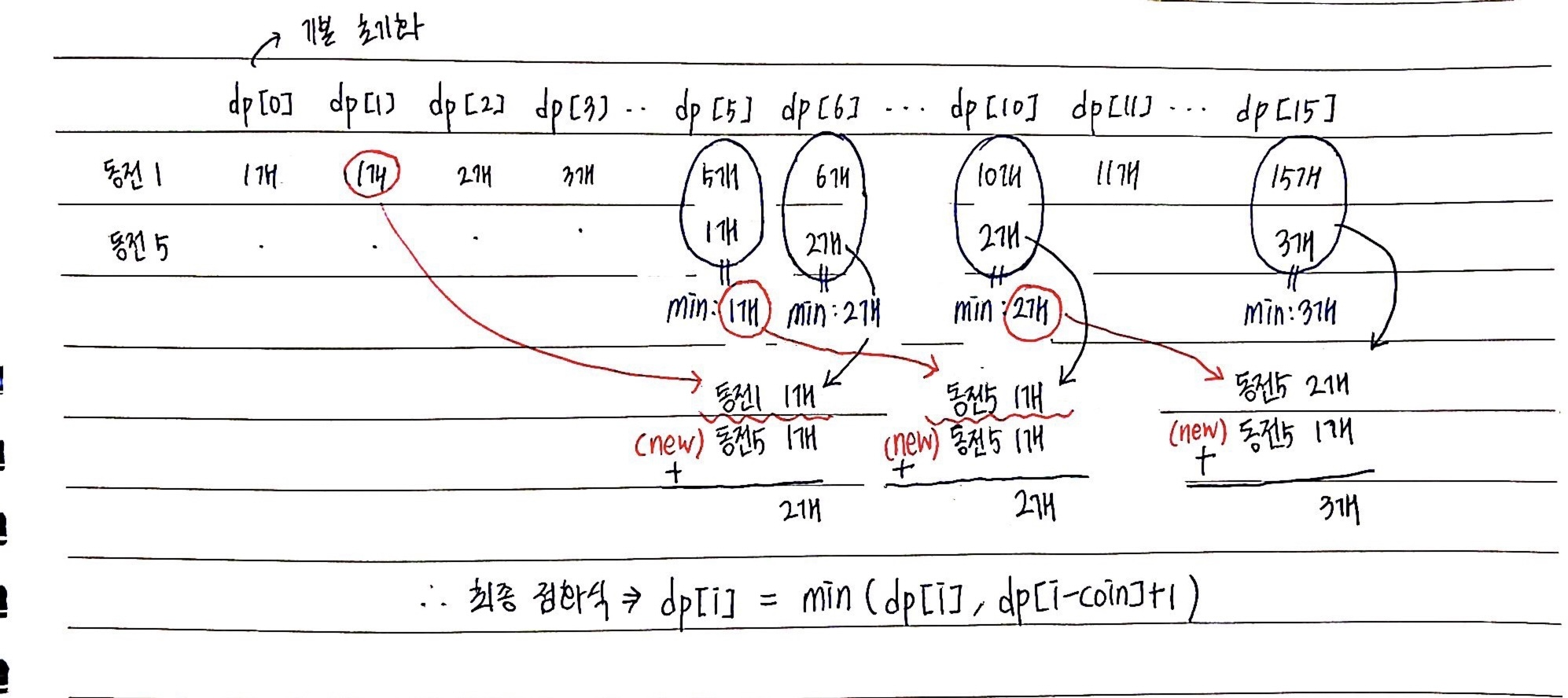
먼저 동전 1을 통해 1원~10원까지 만들 수 있는 동전 최소 개수는 각각 1,2,3,...,10이다. 따라서 dp[i]=i로 갱신된다.
이제 동전 5가 추가되었다고 해보자. 5원짜리 동전을 가지고 1~4의 값을 나타낼 순 없으므로 dp[1]에서 dp[4]까지의 값은 더 이상 갱신되지 않으며, 이는 곧 dp값이 확정되었다고 해석할 수 있다.
자 그럼 다시, 동전 5가 추가된 상태에서 5원을 만들어보자. 기존에 dp[5]는 1원만 갖고 있었으므로 5개가 필요했다. 하지만 5원이 추가되었으므로 5원 1개만으로 5원을 만들 수 있다. 여기서 우리는 dp[i]값은 기존값과 현재값의 min값으로 계속해서 갱신된다는 것을 알 수 있다.
이제 뼈대는 잡혔고, 이어서 6원을 만드는 경우도 생각해보자. 기존 dp[6]은 1원만 갖고 있었으므로 6개가 필요했다. 하지만 5원이 추가되었으므로 1원 1개 + 5원 1개로 6원을 만들수 있다. 이는 1원을 만들 수 있는 최소 개수(=dp[1])에서 현재 추가된 새로운 동전 5원을 더해준 행위이다. 여기서 우리는 동전 5원을 더해준다고 해서 개수가 5로 늘어나는 것이 아니라 5원짜리 동전 '1개'가 추가된다는 것을 알아야한다. 즉 dp[6]=dp[1]+1 이란 뜻이며, dp값은 기존 값과 현재값의 min값으로 계속해서 갱신된다는 것을 알수 있다.
결국 이를 점화식으로 표현하면,
dp[i] = min(dp[i],dp[i-coin]+1)
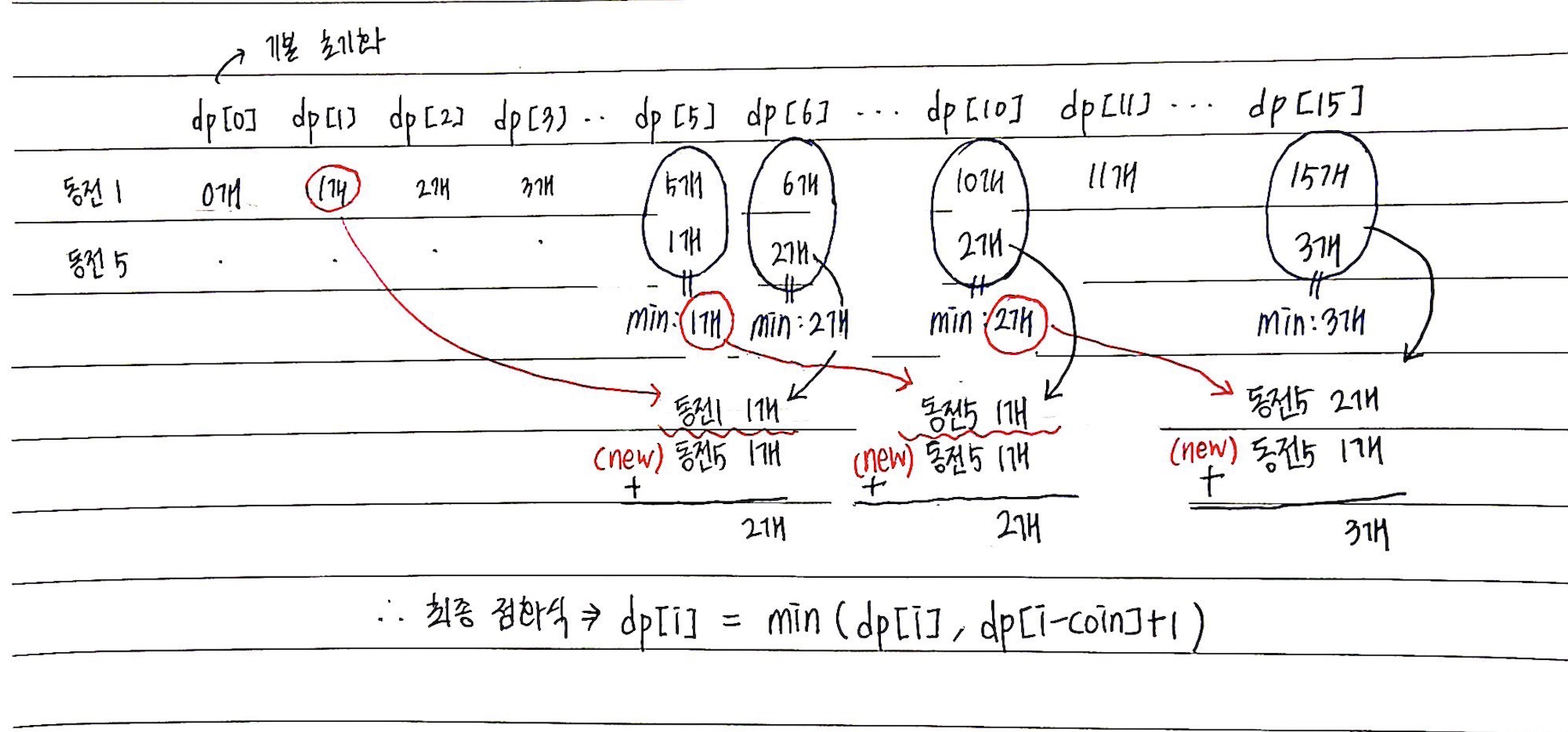
이다. 설명이 부족하다면 아래 그림을 확인해보자. dp[6]과 dp[10] 그리고 dp[15]과정도 다시 한 번 확인해보자.
for _ in range(n):
arr.append(int(input()))
dp = [100001 for i in range(k + 1)]
dp[0] = 0
for coin in arr:
for i in range(coin, k + 1): # 현재 갖고 있는 동전 i를 기준으로 i 미만의 값은 갱신될리 없으므로 i부터 시작.
dp[i] = min(dp[i], dp[i - coin] + 1)
if dp[k] == 100001:
print(-1)
else:
print(dp[k])
점화식은 눈으로 보고 반복해야만 보인다 ! 명심명심