우리는 이미 이전 포스팅에서 최단 경로(거리) 문제의 대표적인 알고리즘인 다익스트라 알고리즘에 대해 배웠다. 다익스트라 알고리즘의 특징 중 하나는 음의 간선이 없을 때만 정상 동작한다는 것이다. 그렇다면 간선이 음의 비용을 갖고 있다면 어떻게 최단 경로를 알아낼 수 있을까? ( 다익스트라 알고리즘을 모른다면 이전 포스팅을 보고 오는 것을 추천한다 🤗 )
벨만 포드 알고리즘
개요
백준의 타임머신 문제를 보면 특정 도시에서 다른 도시를 이동할 때 걸리는 시간이 양수가 아닌 경우가 있다. 순간 이동을 하는 경우는 시간을 0으로, 또 타임머신을 타고 이전으로 돌아가는 경우는 시간이 음수값이 되기도 한다. 이러한 상황이 음의 간선이 포함되었을 때 최단 경로를 구하는 문제 예시 중 하나라고 볼 수 있다.
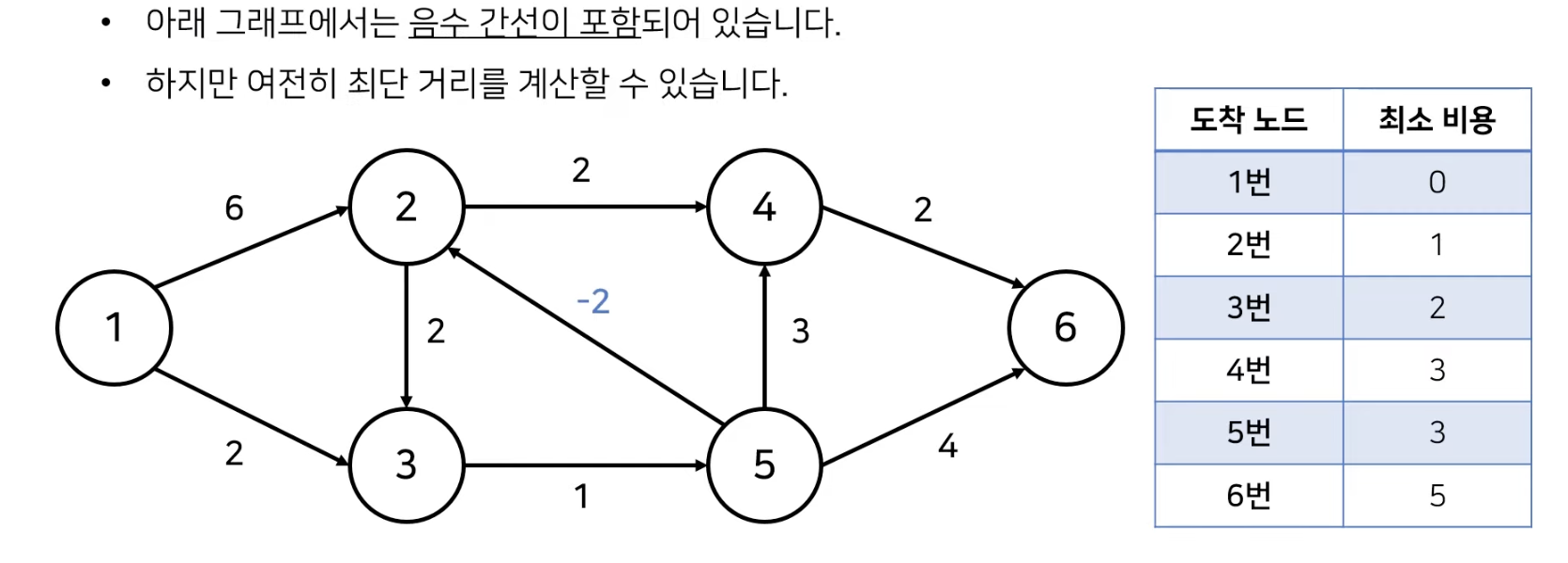
위 그림을 보면 음수 간선이 포함되어 있더라도 우리가 이미 알고있는 다익스트라 알고리즘 동작 과정을 통해 1번 노드로부터 시작되는 각 노드들의 최단 거리 (최소 비용)을 구할 수 있다.
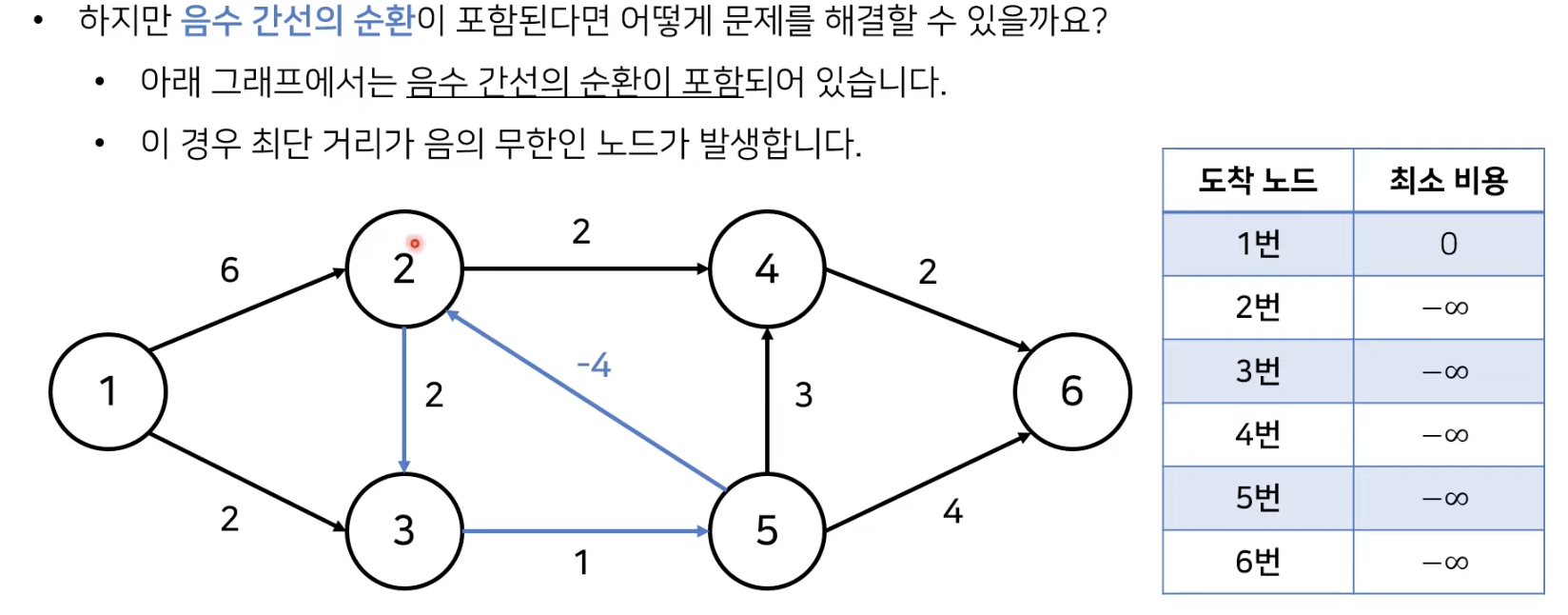
하지만 간선 정보에 따라 최소 비용을 결정하지 못하는 경우도 존재하는데, 그 예가 바로 위 그림의 경우이다. 우리는 파란 선으로 되어있는 음수 간선의 사이클을 통해 비용을 무한히 줄여나갈 수 있다. 결국 음수 간선 사이클이 발생하면 최소 비용을 결정짓지 못하고 최소 비용이 음의 무한값으로 빠지게 된다. 이렇게 되면 궁극적으로 다익스트라 알고리즘을 음의 간선이 있는 그래프 전체에 적용시킬 수 없다.
특징
먼저 최단 경로 문제는 다음과 같은 상황에 따라 분류하여 생각해볼 수 있다.
- 모든 간선이 양수인 경우
- 음의 간선이 존재하는 경우
- 음수 간선 순환이 없는 경우
- 음수 간선 순환이 있는 경우
- 벨만 포드 알고리즘은 음의 간선이 포함된 상황에서도 최단 경로를 찾을 수 있다. (위의 모든 경우 커버 가능)
- 음수 간선의 순환을 감지할 수 있다.
- 벨만 포드 알고리즘의 기본적인 시간 복잡도는
O(EV)이므로 다익스트라 알고리즘의 시간복잡도인O(ElogV)보다 느리다 (그래서 보통 모든 간선이 양수인 경우에는 성능을 위해 다익스트라 알고리즘을 쓰는 것이 낫다)
동작 과정
- 출발 노드를 설정한다.
- 최단 거리 테이블을 초기화한다.
- 아래의 과정을
n-1번 반복한다.- 전체 간선 E개를 하나씩 확인한다.
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 만약 음의 순환이 발생하는지 체크하고 싶다면 3번 과정을 한 번 더 반복한다
- 음의 순환이 발생하지 않는다면 정상적으로 최종 최단 거리 테이블을 완성한 것이므로 3번 과정을 반복하더라도 최단 거리 테이블의 값이 갱신되지 않을 것이다
- 최단 거리 테이블의 값이 갱신된다면 음의 순환이 존재한다는 것이다.
구현 코드
import sys
input = sys.stdin.readline
INF = int(1e9)
n, m = map(int, input().strip().split())
edges=[]
distance=[INF]*(n+1)
for _ in range(m):
a, b, c = map(int, input().split())
edges.append((a, b, c))
def bf(start):
distance[start]=0
for i in range(n):
for j in range(m):
cur_node= edges[j][0]
next_node= edges[j][1]
cost= edges[j][2]
if distance[next_node] > distance[cur_node]+cost:
distance[next_node]=distance[cur_node]+cost
if i==n-1:
return True
return False
negative_cycle=bf(1)
if negative_cycle:
print(-1)
else:
for i in range(2,n+1)
if distance[i]==INF:
print(i,'까지의 최단 거리:도달불가')
else:
print(i,'까지의 최단 거리:',distance[i])
벨만 포드 알고리즘 vs 다익스트라 알고리즘
- 다익스트라 알고리즘
- 매번 방문하지 않은 노드 중 가장 최단 거리가 짧은 노드를 선택한다
- 음수 간선이 없다면 빠르게 최적의 해를 구할 수 있다
- 벨만 포드 알고리즘
- 매번 간선 정보를 모두 확인한다
- 즉 벨만 포드 알고리즘이 다익스트라 알고리즘의 상위 집합 느낌이라고 생각하면 된다 (다익스트라 알고리즘의 최적의 해를 항상 포함하므로 ⭐️)
- 다익스트라 알고리즘에 비해 시간이 느리지만, 음수 간선 사이클 존재여부까지 확인해 볼 수 있다

정리가 잘 된 글이네요. 도움이 됐습니다.