💡 크루스칼 알고리즘을 완전히 이해하기 위해선 서로소 집합 자료구조의 동작원리(find 연산, union 연산)에 대해 필수적으로 알아야한다. 아직 서로소 집합 자료구조의 개념을 잘 모른다면 해당 포스팅 을 보고 숙지해보자 !
신장 트리
크루스칼 알고리즘은 최소 신장 트리를 찾기 위해 사용되는 알고리즘 중 하나이다. 여기서 신장 트리란 그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
예를 들어 아래와 같이 G라는 그래프가 있을 때
이 G 그래프에서 발생할 수 있는 신장 트리는 다음과 같다.

즉 각 노드들 간에 서로 연결은 되어 있으나, 자기 자신으로 돌아오는 또 다른 간선이 있어선 안된다. (사이클 X) 이러한 조건은 트리의 조건 이기도 하다.
최소 신장 트리
앞서 보았듯이 신장 트리는 여러 가지 형태로 표현될 수 있다. 그러나 만약 노드들간의 간선 비용이 존재한다면, 가장 최소한의 비용으로 구성된 단 하나의 신장 트리를 구할 수 있을 것이다. 이는 어떻게 구할 수 있을까?
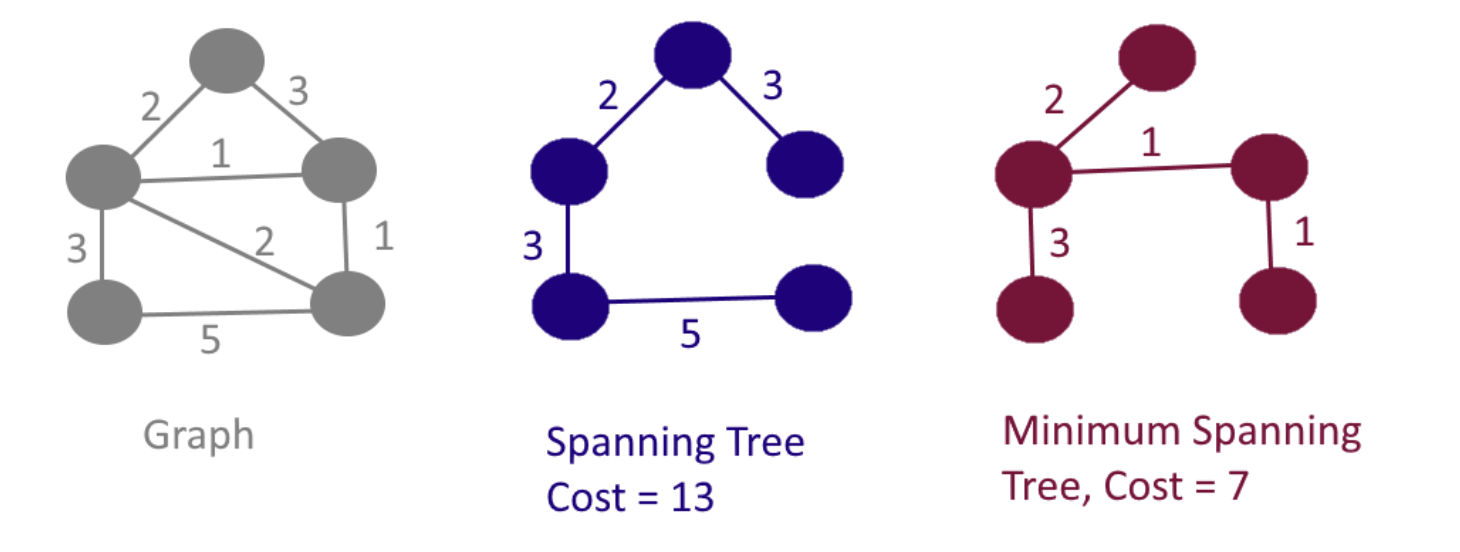
위 사진을 보면 가능한 신장 트리는 가운데 트리와 오른쪽 트리 모두 될 수 있지만, 그 중 최소의 간선 비용을 들여서 만든 트리는 오른쪽 트리가 될 것이다.
이렇게 최소 신장 트리를 찾기 위해 사용되는 대표적인 알고리즘이 크루스칼 알고리즘이다.
크루스칼 알고리즘
- 대표적인 최소 신장 트리 알고리즘이다.
- 매번 가장 적은 비용으로 모든 노드를 연결할 수 있도록 하는 특성 때문에 그리디 알고리즘으로 분류된다.
- 구체적인 동작과정은 다음과 같다.
- 간선 정보를 비용에 따라 오름차순으로 정렬 한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는 지 확인한다.
- 사이클이 발생하지 않는 경우 최소 신장 트리에 해당 간선을 포함시킨다.
- 사이클이 발생하는 경우 최소 신장 트리에 해당 간선을 포함시키지 않는다.
- 모든 간선에 대하여 2번 과정을 반복한다.
결국 쉽게 생각하면 사이클 발생 여부를 통해 현재 간선을 최소 신장트리로 포함시킬지 여부를 결정하는 행위를 반복하면 되는것이다. 그렇다면 사이클 발생 여부는 어떻게 판단할 수 있을까?
현재 간선이 갖고 있는 a, b 노드의 부모 노드를 확인했을 때 두 부모 노드가 같다면 사이클이 발생하고 그렇지 않다면 사이클이 발생하지 않는다. 왜 그런지에 대한 답은 이 포스팅 에서 찾을 수 있을 것이다. (간단히 말하면 a, b는 이미 같은 집합에 포함되었기 때문임 🤗)
아, 참고로 최종적으로 완성된 최소 신장 트리의 간선의 개수는 V-1이다 (여기서 V는 노드의 개수를 의미) 항상 노드의 총개수 -1 임을 잊지 말자.
코드 구현
서로소 집합 자료구조 구현의 기본이 되는 find, union 연산 함수에서 간선을 비용순 정렬한 뒤 사이클 반펼 로직만 추가하면 매우 쉽게 구현할 수 있다.
import sys
input = sys.stdin.readline
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
print("find_parent", parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
v, e = map(int, input().strip().split())
parent = [0] * (v + 1)
edges = []
for i in range(1, v + 1):
parent[i] = i
for _ in range(e):
a, b, cost = map(int, input().strip().split())
edges.append((cost, a, b))
edges.sort()
mst=[]
result = 0
for edge in edges:
cost, a, b = edge
if find_parent(parent, a) != find_parent(parent, b):
# (1) 보통 이렇게 mst의 세부 간선들을 리스트화해서 보여주거나,
mst.append(edge)
union_parent(parent, a, b)
# (2) mst의 간선 비용의 합을 구하기도 한다
result += cost
print(result)
print(mst)백준 문제
- https://www.acmicpc.net/problem/1197 (테크닉 없이 크루스칼 알고리즘을 코드로 그대로 구현하면 되는 문제)
