최소 신장 트리의 대표 알고리즘인 Prime 알고리즘에 대해 알아보자. 최소 신장 트리 개념은 이전 포스팅에 정리해두었으니 아직 잘 모르겠다면 이전 포스팅 을 보고 숙지해보자
Prime 알고리즘
- 대표적인 최소 신장 트리 알고리즘 중 하나이다.
- 크루스칼 알고리즘
- 프림 알고리즘
- 프림 알고리즘
- 시작 정점(노드)을 선택한 후, 정점에 인접한 간선 중 최소 비용의 간선으로 연결된 정점을 선택한다. 이후 해당 정점에서 또 다시 최소 간선으로 연결된 정점을 선택하는 방식으로 최소 신장 트리를 확장해가는 방식이다.
- 크루스칼 알고리즘 vs 프림 알고리즘
- 일단 공통점으로는 그리디 알고리즘 을 기초로 하고 있다. 당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾아내기 때문이다.
- 크루스칼 알고리즘은 정렬을 통해 모든 노드에 대하여 가장 가중치가 작은 간선부터 선택하면서 최소 신장 트리를 구하는 반면,
- 프림 알고리즘은 특정 노드에서 시작, 해당 정점에 연결된 간선들 중 가장 가중치가 작은 간선을 선택하는 방식으로 최소 신장 트리를 구한다.
- 크루스칼 알고리즘은 부모 노드 비교, 프림 알고리즘은 집합 내 원소 비교를 통해 궁극적으로 사이클 발생 여부를 확인한다는 점에서 공통점이 있다. (= 동작 과정은 다르나 얻고자 하는 바가 같음)
동작 과정
- 임의의 정점을 선택하여 '연결된 노드 집합'에 삽입한다.
- 선택된 정점에 연결된 간선들을 '간선 리스트'에 삽입한다.
- 간선 리스트에서 최소 가중치를 갖는 간선부터 추출해서,
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 이미 들어 있다면, 스킵한다 (cycle 발생을 막기 위해)
- 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 들어있지 않다면, 해당 간선을 선택하고 해당 간선 정보를 '최소 신장 트리(mst)'에 삽입한다
- 이후, 간선에 연결된 인접 정점의 간선들 중 '연결된 노드 집합'에 없는 노드와 연결된 간선들만 간선 리스트에 삽입- 선택된 간선은 '간선 리스트'에서 제거한다.
- 간선 리스트에 더 이상의 간선이 없을 때까지 2~4를 반복한다.
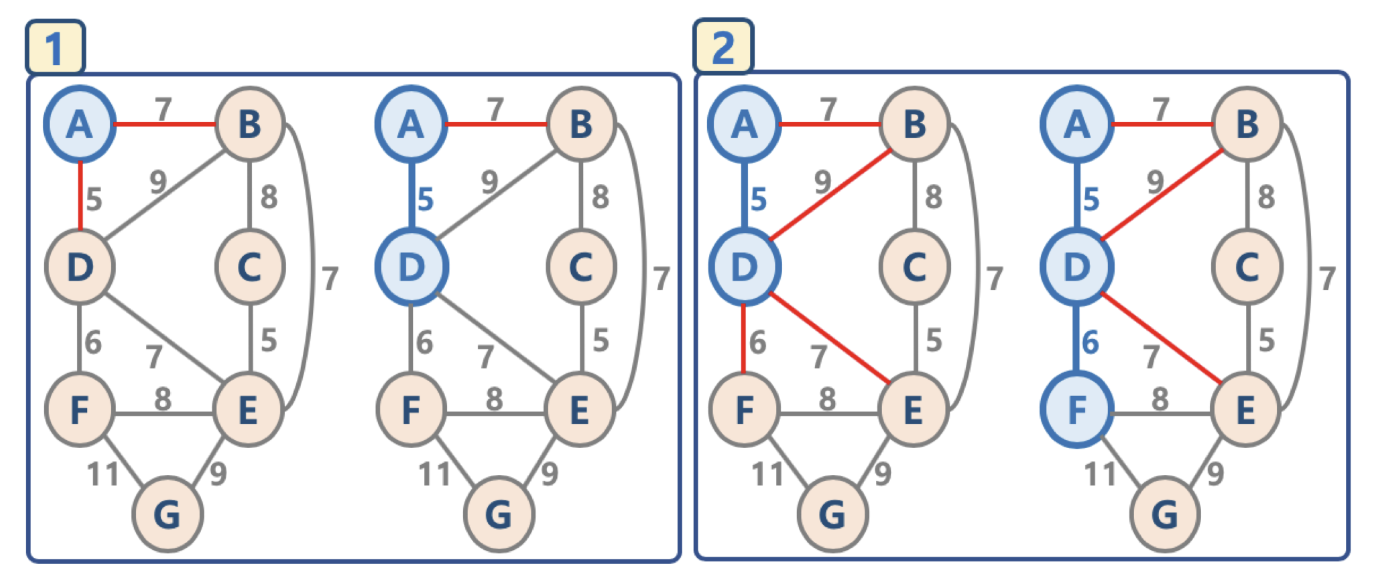

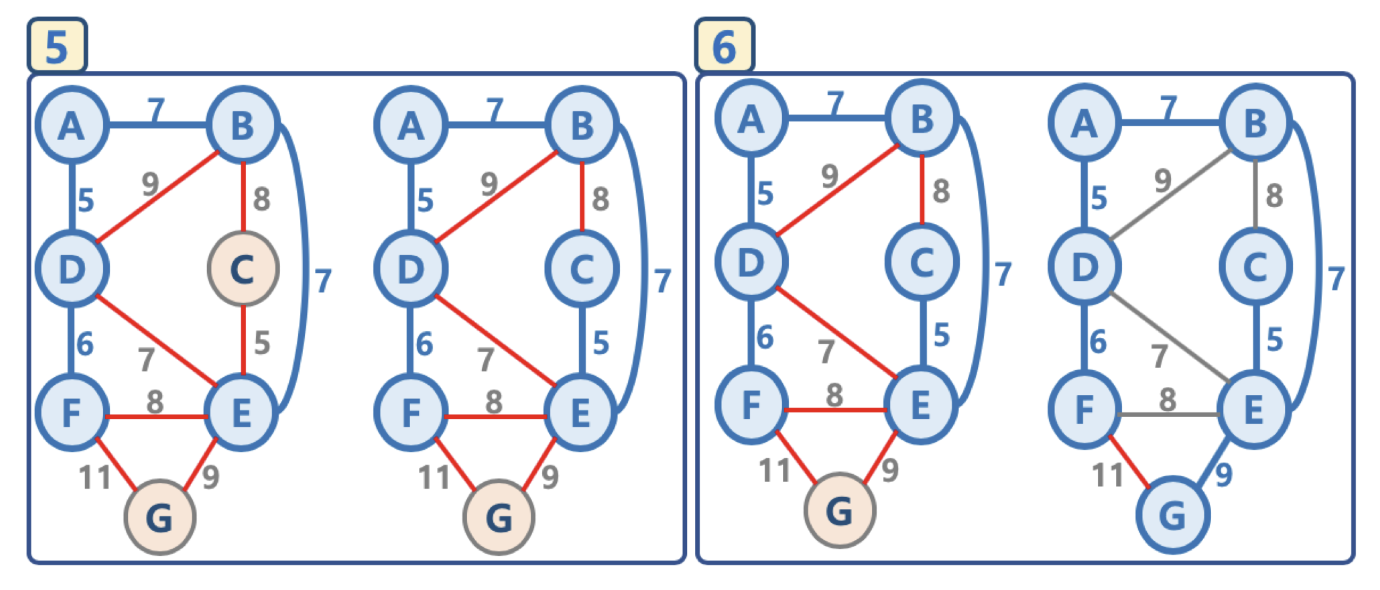
(그림 출처 : 잔재미코딩)
코드 구현
본격적으로 프림 알고리즘을 구현하기 전에, 해당 구현을 python에서 간단하고 빠르게 구하기 위해 알아두면 좋을 두 가지 라이브러리를 짚고 넘어가보자.
참고 1 | heap라이브러리를 활용한 우선순위 큐 사용
-
우선순위 큐는 우선순위가 가장 높은 data를 가장 먼저 꺼낼 수 있는 자료구조이며, 파이썬에서는 heapq 라이브러리로 정의해두었다. 해당 자료구조는 삽입, 삭제 모두 O(logN)으로 빠른 연산 속도를 보여준다.
-
아무튼 요지는, 해당 라이브러리를 사용하면 가중치가 작은 것부터 우선적으로 쉽게 값을 참조하고 뽑아쓸 수(pop) 있어 프림 알고리즘을 구현하는 데 굉장히 유횽하다
-
참고로 heapq 내장 함수인 heapify 함수는 입력으로 받은 list 데이터를 자동으로 한 번에 heap 형태로 변환해주어 우선순위 큐로 사용할 수 있다.
import heapq
graph_data=[[2,'A'],[5,'B'],[3,'C']]
heapq.heapify(graph_data)
# 결과: [[2,'A'],[3,'C'],[5,'B']참고 2 | collections 라이브러리의 defaultdict 함수 활용하기
defaultdict 함수는 key에 대한 value를 지정하지 않아도 자동으로 빈 리스트로 초기화해줄 수 있다
from collections import defaultdict
list_dict = defaultdict(list)
print(list_dict[key1])
# 결과 : [] 빈 리스트 나오는 것이 정상이제 위의 동작 과정 단계에 맞추어 실제로 코드를 구현해보자
-
일단 아래와 같이 간선 정보가 리스트 형태로 저장되어있다고 가정한다
myedges = [ (7, 'A', 'B'), (5, 'A', 'D'), (8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E'), (5, 'C', 'E'), (7, 'D', 'E'), (6, 'D', 'F'), (8, 'E', 'F'), (9, 'E', 'G'), (11, 'F', 'G') ] -
그리고 기본적으로 변수 설정 및 초기화를 해준다
from collections import defaultdict from heapq import * def prim(start_node, edges): mst = list() adjacent_edges = defaultdict(list) for weight, n1, n2 in edges: adjacent_edges[n1].append((weight, n1, n2)) adjacent_edges[n2].append((weight, n2, n1)) connected_nodes = set(start_node) candidate_edge_list = adjacent_edges[start_node] heapify(candidate_edge_list)-
최종적인 결과값을 반환할 리스트
mst -
모든 쌍방(무방향) 간선 정보들을 저장할
adjacent_edges( defaultdict 사용 ) -
연결된 노드들을 저장할(= 연결된 노드 집합)
connected_nodes -
후보군 간선들을 저장할(= 간선 리스트)
candidate_edge_list( 우선순위큐-최소힙으로 정의 -> 여기서 최소 비용을 갖는 간선을 빠르게 찾아야하기 때문에)중간에 for문으로 간선 정보들을 저장하는 이유는 어떤 노드를 시작으로 접근하더라도, 해당하는 간선 정보를 불러올 수 있도록 하기 위해서이다. 예를 들어 입력으로 받는 그래프 간선 정보 중 (7, a, b)가 존재할 때, adjacent_edges에서는
adjacent_edges[a]=[(7,a,b),..]adjacent_edges[b]=[(7,b,a),...]로 저장되어 있을 것이다. 이렇게 해야만 인접 간선 정보가 누락되지 않고 최소 간선 트리를 찾아낼 수 있다.
-
-
핵심 알고리즘을 구현한다
while candidate_edge_list: cost, n1, n2 = heappop(candidate_edge_list) if n2 not in connected_nodes: connected_nodes.add(n2) mst.append((cost,n1,n2)) for edge in adjacent_edges[n2]: if edge[2] not in connected_nodes: heappush(candidate_edge_list,edge) return mst동작 과정을 그대로 코드로 변환시키면 되므로 코드 자체는 매우 간결하다.
다시 말로 풀어 설명하면,
먼저 간선리스트(candidate_edge_list)에 저장된 후보 간선들 중 가장 비용이 작은 것을 pop한다.
pop한 간선 정보(cost, n1 -> n2)에 대해서 새롭게 잇게 되는 노드인 n2가 아직 연결된 노드 집합(connected_nodes)에 저장되지 않았다면 해당 노드를 집합에 저장하고, 해당 간선 정보를 최소 신장 트리(mst)에 삽입한다. 이후 방금 저장한 노드에 연결되어 있는 간선 정보들을 간선 리스트에 저장해준다. 이 때, 연결된 노드 집합에 없는 노드와 연결된 간선들만 간선 리스트에 삽입하여 불필요한 삽입을 무시할 수 있도록 한다. 간선리스트가 비워질 때까지 위 과정을 반복하면, 최소신장트리를 완성시킬 수 있다. -
결과
prim('A',medeges) #[(5, 'A', 'D'), (6, 'D', 'F'), (7, 'A', 'B'), (7, 'B', 'E'), (5, 'E', 'C'), (9, 'E', 'G')]참고로 프림알고리즘의 시간 복잡도는 while문을 통해 모든 간선에 대해 반복하고(최악의 경우), 최소힙 구조를 통해 candidate_edge_list 원소를 pop하므로 최종 O(ElogE)의 빠른 시간 복잡도를 가진다. 이를 개선하여 O(ElogV)의 시간 복잡도를 가진 프림알고리즘도 있긴 하지만, 이는 기회가 될 때 다음에 다루도록 하겠다 🥲 아래는 전체 코드이다.
from collections import defaultdict
from heapq import *
def prim(start_node, edges):
mst = list()
adjacent_edges = defaultdict(list)
for weight, n1, n2 in edges:
adjacent_edges[n1].append((weight, n1, n2))
adjacent_edges[n2].append((weight, n2, n1))
connected_nodes = set(start_node)
candidate_edge_list = adjacent_edges[start_node]
heapify(candidate_edge_list)
while candidate_edge_list:
weight, n1, n2 = heappop(candidate_edge_list)
if n2 not in connected_nodes:
connected_nodes.add(n2)
mst.append((weight, n1, n2))
for edge in adjacent_edges[n2]:
if edge[2] not in connected_nodes:
heappush(candidate_edge_list, edge)
return mst
알고리즘 이름 Prim이에요!