빅오 표기법 (Big-O notation)

본 포스트는 윤성우님의 열혈 자료구조를 출처로 작성된 글입니다.
필자의 복습을 위한 요약 주 목적이며 따라서 생략된 부분이 많을 수 있습니다. 오타나 잘못된 내용이 발견될 시 답글로 남겨주시면 감사하겠습니다.

상수

앞서 이진탐색에서 최악의 경우 시간복잡도를 평가할때 상수 $1$을 버렸다. 이렇게 상수를 버리는게 시간복잡도 평가에서는 왜 합리적인 것으로 평가될까?

앞서 시간복잡도는 데이터의 수 $n$이 증가할때 최악의 경우 이 알고리즘이 어떤 패턴을 보이는가(즉, 효율적인 패턴을 보이는가)가 주된 관심사이다.

따라서 $n$에 대한 식으로 정리되는 시간복잡도에서 $n$이 급격하게 증가하면 상수는 큰 의미를 갖지 않게 된다.

$n$이 $1,000,000$정도의 크기라고 해보자. 우리가 앞서 이진탐색의 성능평가에서 버린 상수 1은 $0.000001$의 비중밖에 차지하지 않는다.

만약 상수가 $1,000,000$라면 된다면? $n$이 $1$이더라도 연산을 백만번이나 하는 매우 비효율적인 알고리즘이니 애초에 고려의 대상이 아니다.

빅오 표기법

빅오 표기법(Big-O notaion)은 어떤 알고리즘의 시간복잡도 $T(n)$에서 실제로 가장 크게 영향력을 끼치는 부분을 기준으로 알고리즘의 성능을 표현하는 표기법이다.

이전에 다룬 이진탐색의 시간복잡도 $T(n)$은 $log_2n+1$이었다. 앞서 상수는 시간복잡도에서 큰 의미를 갖지 않는다는 것을 밝혔으니 이진탐색의 빅오는 $log_2n$이다.

만약 어떤 알고리즘의 시간복잡도 $T(n)$이 $n^2 + 2n +1$라면, 이 알고리즘의 빅오는 어떠할까?
이는 곧, 위의 $T(n)$에서 어떤 항이 $n$이 증가할때 결과에 가장 큰 영향을 미치는지 질문하는 것과 같다!

다음의 표를 보자. ( 열혈 자료구조 저자 윤성우님의 자료입니다.)

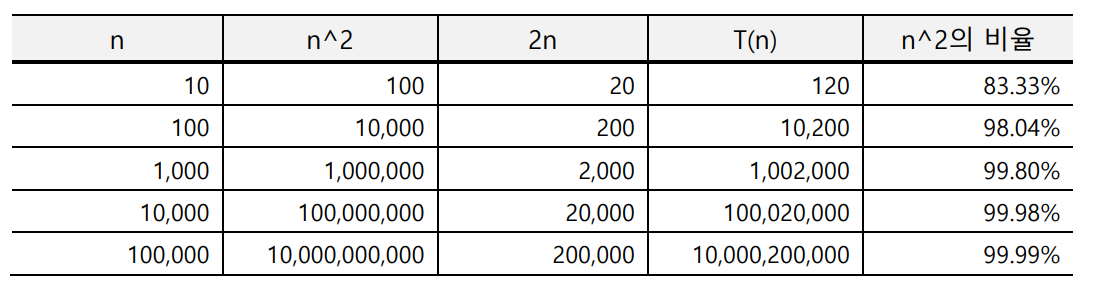
위 표는 $T(n) = n^2 + 2n +1$에서, $n^2$과 $2n$이 결과에 얼마나 영향을 미치는지를 정리했다.
$n$이 커질수록 $n^2$이 결과에서 차지하는 비율이 매우 커짐을 알 수 있다.

따라서
빅오표기법에서는 시간복잡도 $T(n)$이 다항식으로 표현이 된 경우 최고차항을 빅오로 삼는다.

• 그렇다면 각 항의 계수(Coefficient)는 어떻게 할 것인가?
  빅오에서 중요하게 생각하는 것은 수 자체가 아니라 그래프의 패턴이다. 계수는 그래프의 패턴에는 영향을 미치지 않으므로 고려하지 않는다.

그래프의 패턴은 대표적으로 아래의 경우가 있다.

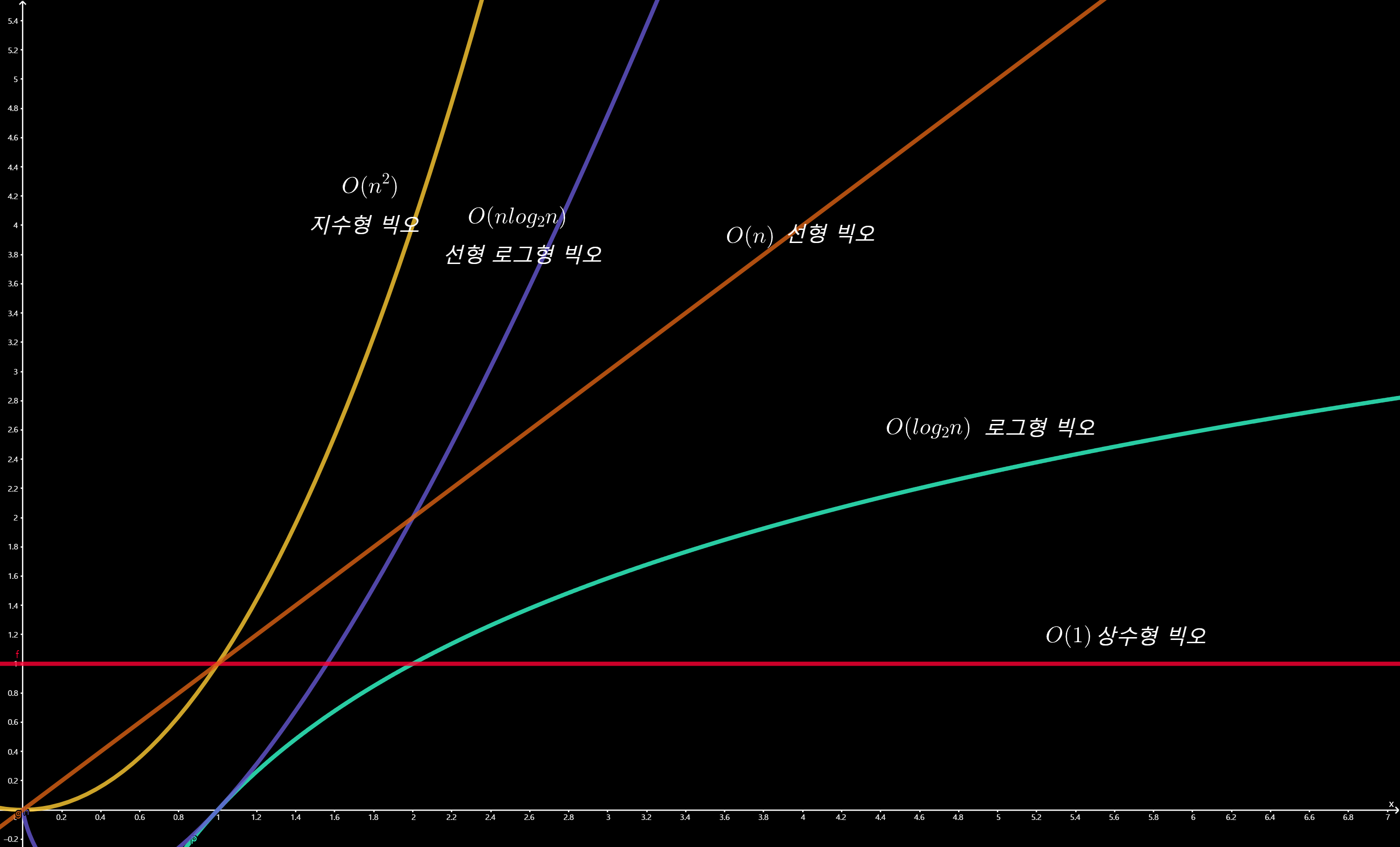
이중 쓸만한 빅오는 로그형 빅오부터라고 일반적으로 평가한다.
반면 어떤 알고리즘이 지수형 빅오를 갖는다면 반드시 수정되어야 하거나 그만큼의 성능을 감수하고서라도 사용하는 경우이다.

빅오에 대한 엄밀한 수학적 정의

두 개의 함수 $f(n)$과 $g(n)$이 주어졌을 때, 모든 $n \ge K$에 대하여, $f(n)\le Cg(n)$을 만족하는 두개의 상수 $C,K$가 존재하면, $f(n)$의 빅오는 $O(g(n))$이다.

즉, $g(n)$에 임의의 스칼라곱($C$)C을 했을때, $f(n)$보다 어느 지점에서($K$), $Cg(n)$이 항상 더 크다면, 빅 오는 $g(n)$을 기준으로 하겠다는 의미이다.

빅오 표기법의 핵심은 그래프의 패턴의 비교이다! 즉 임의의 스칼라곱($C$)를 하더라도, 일정 증가율의 패턴을 넘지 못한다면, 빅오는 그 증가율을 보이는 함수를 취한다는 것이다.

$n^2$에 어떤 스칼라곱을 취해도($Cn^2$), 어느 지점($K$)에서는 $n^3$의 증가율에 밀린다.

빅오는 최악의 경우의 연산횟수를 나타내는 다항식이 보여주는 증가율의 상한선을 표현하는 표기법으로 이해할 수 있다.

이해를 돕기 위해 예제를 보자.

$Eg)$

$T(n) = 7n^3 +3n^2 +2$ 일 경우,
$f(n) = T(n), \ G(n) = n^3$으로 두자.

1. $n \ge 0$일때, $7n^3 \le 7G(n)$이다.
2. $n \ge 3$일때, $3n^2 \le 3G(n)$이다.
3. $n \ge 2$일때, $2 \le 2G(n)$이다.

즉, $n\ge3$일때, $7n^3 + 3n^2 + 2 \le 7G(n) +3G(n) + 2G(n) = 12G(n)$이므로,

$K = 3,\ C=12$일때, $f(n) \le CG(n)$이다.

따라서 $T(n)$의 빅오 표기법은 $O(n^3)$이다.

위의 예제는 $n^3$에 계수를 곱하고 다른 항을 다항식 $T(n)$도 결국 $n^3$인 빅오의 패턴을 넘어서지 못함을 보이고 있다..