CPSC 223 - Red-black trees

rhkr9080·2023년 6월 30일

CPSC 223 : https://zoo.cs.yale.edu/classes/cs223/f2022/index.html
Data Structures and Programming Techniques : http://www.cs.yale.edu/homes/aspnes/classes/223/notes.html
2-3 trees : http://cs.yale.edu/homes/aspnes/classes/223/notes.html#A2.2BIBM-3_trees
Red-black trees : http://cs.yale.edu/homes/aspnes/classes/223/notes.html#redBlackTrees

2-3 trees

An early branch in the evolution of balanced tree was the 2-3 tree. Here all paths have the same length, but internal nodes have either 2 or 3 children. The maximum path length in a tree with n nodes is at most logn, as in a perfectly balanced binary tree.

An internal node in a 2-3 tree holds one key if it has two children and two if it has three children. A search that reaches a three-child node must compare the target with both keys to decide which of the three subtrees to recure into.

Insertion is done by expanding leaf nodes. This may cause a leaf to split when it acquires a third key. When a leaf splits, it becomes two one-key nodes and the middle key moves up into its parent. The tree grows in height by adding a new root when the old root splits.

ref)
2-3 Tree Insertion : https://www.youtube.com/watch?v=bhKixY-cZHE
2-3 Tree : https://www.geeksforgeeks.org/2-3-trees-search-and-insert/

Red-black trees🔴⚫

2-3-4 tree is good, but it is not binary. We are fond of binary trees. Can we represent a 2-3-4 tree in a binary way? 😄 Obama has told you: yes, we can.
RBtree is simple, absorb all red nodes into their parents, they are just 2-3-4 trees!
https://yuyuan.org/RedBlackTreeTutorial

1. 모든 노드는 빨간색 혹은 검은색
2. 루트 노드는 검은색
3. 모든 리프 노드(NIL)들은 검은색
4. 빨간색 노드의 자식은 검은색 (No two red nodes are adjacent)
5. 모든 리프 노드에서 Black Depth는 같다.

The RedBlack tree acts in a way to keep the overall tree fairly balanced as new data is loaded in.

A red-black tree is a 2-3-4 tree (i.e. all nodes have 2,3, or 4 children and 1,2, or 3 internal keys) where each node is represented by a little binary tree with a black root and zero, one, or two red extender nodes as follows.

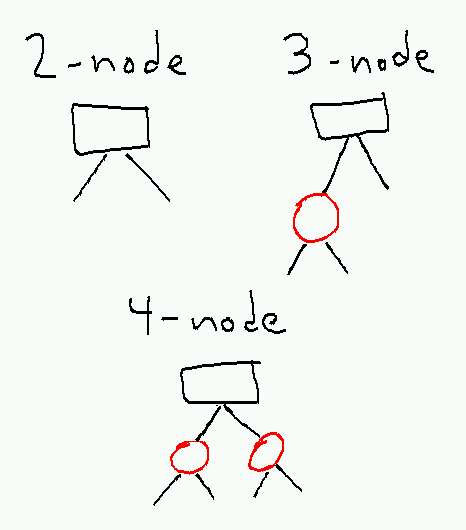
The invariant for a red-black tree is that

1. No two red nodes are adjacent.
2. Every path contains the same number of black nodes.

For technical reasons, we include the null pointers at the bottom of the tree as black nodes; this has no effect on the invariant, but simplifies the description of the rebalancing procedure.

Searching in a red-black tree is identical to searching in any other binary search tree; we simply ignore the color bit on each node. So search takes O(log n) time. For insertions, we use the standard binary search tree insertion algorithm, and insert the new node as a red node.

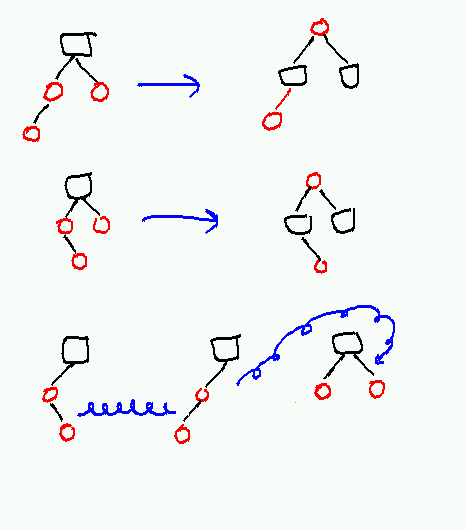
🚀 구현

Search

node *search(node *x, int v)
{
	if (x == NULL)
    	return 0;
    
    if (v < x->data)
    	search(x->left, v);
    else if (v > x->data)
    	search(x->right, v);
    else
    	return x;
}

Rotation

기존의 tree(root, x)에 새로운 subtree(y)를 추가하는 것으로 가정

// Left Rotation
void LeftRotate(struct node **root,struct node *x)
{
    // 새로운 subtree 나(y)를 parent(x)의 right에 추가
    struct node *y = x->right;
 
    // parent의 right과 나의 left를 연결
    x->right = y->left;
 
    // 나와 parent를 연결
    if (x->right != NULL)
        x->right->parent = x;
 
    // 나와 parent의 위치를 바꿈
    y->parent = x->parent;
 
    // parent가 root였으면, 나를 root로 변경
    if (x->parent == NULL)
        (*root) = y;
 
    // 부모 node가 할아버지 node의 왼쪽에 있는 경우
    else if (x == x->parent->left)
        x->parent->left = y;
    // 부모 node가 할아버지 node의 오른쪽에 있는 경우
    else    x->parent->right = y;
 
    // 바뀐 위치의 parent와 나를 연결
    y->left = x;
    x->parent = y;
}
 
 
// Right Rotation (Similar to LeftRotate)
void rightRotate(struct node **root,struct node *y)
{
    struct node *x = y->left;
    y->left = x->right;
    if (x->right != NULL)
        x->right->parent = y;
    x->parent =y->parent;
    if (x->parent == NULL)
        (*root) = x;
    else if (y == y->parent->left)
        y->parent->left = x;
    else y->parent->right = x;
    x->right = y;
    y->parent = x;
}

Insert

새로운 Red 노드를 생성

typedef struct __node {
	int data;
    char color;
    struct __node *left, *right, *parent;
} node;

binary search node의 규칙에 맞게 insert

void insert (node **root, int data)
{
	node *z = (node *)malloc(sizeof(node));
    z->data = data;
    z->left = z->right = z->parent = NULL;
    
    if(*root == NULL)
    {
    	z->color = 'B';
        (*root) = z;
    }
    else
    {
    	node *y = NULL;
        node *x = (*root);
        
        //BST insert 그대로 진행!!
        while(x != NULL)
        {
        	y = x;
            if (z->data < x->data)
        		x = x->left;
            else 
            	x= x->right;
        }
        z->parent = y;
        if(z->data > y->data)
        	y->right = z;
        else
        	y->left = z;
        z->color = 'R';
    
    	// call insertFixUp to fix red-black tree's property
        // if it is violated due to insertion.
        insertFixUp(root, z);
    }
}

Red-Black Tree의 규칙에 맞게 재정렬

void insertFixUp(struct node **root,struct node *z)
{
    // iterate until z is not the root and z's parent color is red
    while (z != *root && z->parent->color == 'R')
    {
        struct node *y;
 
        // Find uncle and store uncle in y
        if (z->parent == z->parent->parent->left)
            y = z->parent->parent->right;
        else
            y = z->parent->parent->left;
 
        // If uncle is RED, do following
        // (i)  Change color of parent and uncle as BLACK
        // (ii) Change color of grandparent as RED
        // (iii) Move z to grandparent
        if (y->color == 'R')
        {
            y->color = 'B';
            z->parent->color = 'B';
            z->parent->parent->color = 'R';
            z = z->parent->parent;
        }
 
        // Uncle is BLACK, there are four cases (LL, LR, RL and RR)
        else
        {
            // Left-Left (LL) case, do following
            // (i)  Swap color of parent and grandparent
            // (ii) Right Rotate Grandparent
            if (z->parent == z->parent->parent->left &&
                z == z->parent->left)
            {
                char ch = z->parent->color ;
                z->parent->color = z->parent->parent->color;
                z->parent->parent->color = ch;
                rightRotate(root,z->parent->parent);
            }
 
            // Left-Right (LR) case, do following
            // (i)  Swap color of current node  and grandparent
            // (ii) Left Rotate Parent
            // (iii) Right Rotate Grand Parent
            if (z->parent == z->parent->parent->left &&
                z == z->parent->right)
            {
                char ch = z->color ;
                z->color = z->parent->parent->color;
                z->parent->parent->color = ch;
                LeftRotate(root,z->parent);
                rightRotate(root,z->parent->parent);
            }
 
            // Right-Right (RR) case, do following
            // (i)  Swap color of parent and grandparent
            // (ii) Left Rotate Grandparent
            if (z->parent == z->parent->parent->right &&
                z == z->parent->right)
            {
                char ch = z->parent->color ;
                z->parent->color = z->parent->parent->color;
                z->parent->parent->color = ch;
                LeftRotate(root,z->parent->parent);
            }
 
            // Right-Left (RL) case, do following
            // (i)  Swap color of current node  and grandparent
            // (ii) Right Rotate Parent
            // (iii) Left Rotate Grand Parent
            if (z->parent == z->parent->parent->right &&
                z == z->parent->left)
            {
                char ch = z->color ;
                z->color = z->parent->parent->color;
                z->parent->parent->color = ch;
                rightRotate(root,z->parent);
                LeftRotate(root,z->parent->parent);
            }
        }
    }
    (*root)->color = 'B'; //keep root always black
}