❓문제 설명

문제 : 백준 11404 플로이드

난이도 : 골드 4

문제 요약
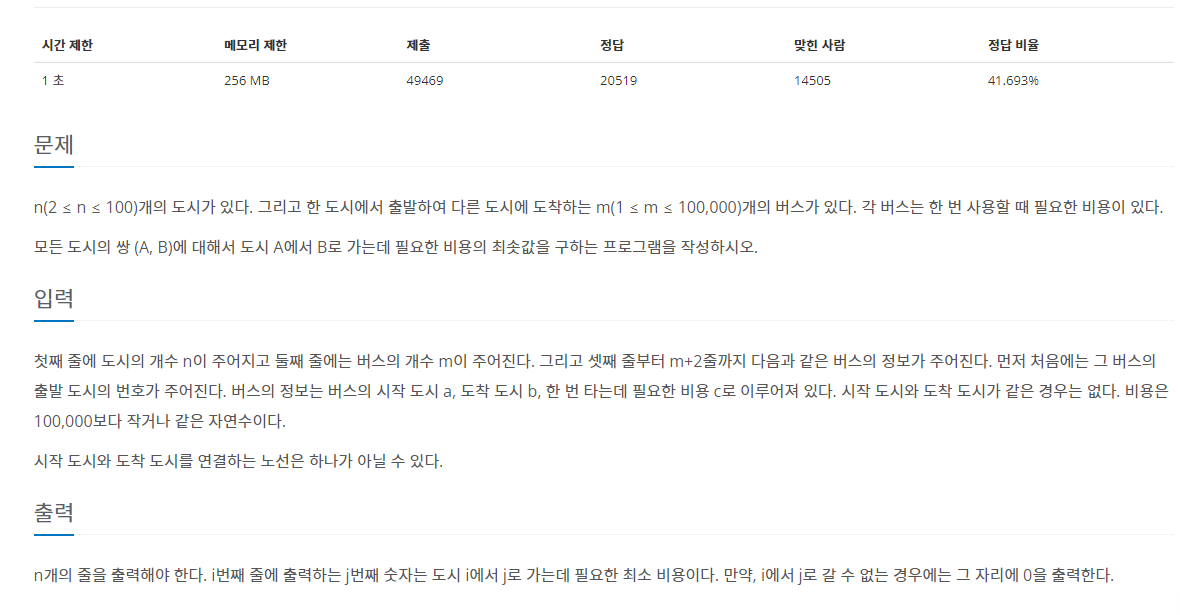
1. n (2 이상 100 이하)개의 도시가 있습니다.
2. 한 도시에서 출발하여 다른 도시에 도착하는 m(1 이상 10만 이하)개의 버스가 있습니다.
3. 각 버스는 한 번 사용할 때 필요한 비용이 있습니다.
4. 모든 도시의 쌍(A,B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구합니다. 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있습니다.

🎯문제 해결 방법

이 문제는 모든 노드 간의 최단 거리를 구해야 하는 문제이므로 문제 제목과 같이 플로이드-워셜 알고리즘을 사용하면 쉽게 풀립니다.

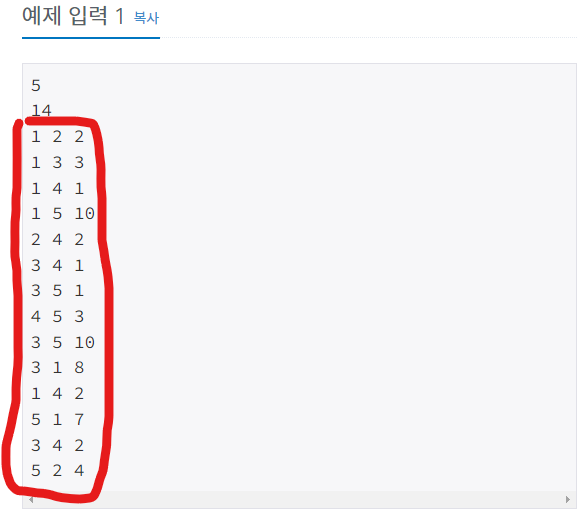
예제를 통해서 설명하겠습니다.

빨간 네모로 친 부분은 한 줄 마다 <시작 노드, 도착 노드, 가중치> 를 입력받습니다.

노드 번호	1	2	3	4	5
1	0	2	3	1	10
2	INF	0	INF	2	INF
3	8	INF	0	1	1
4	INF	INF	INF	0	3
5	7	4	INF	INF	0

가중치를 입력받는 과정에서 중복되는 시작 노드와 도착 노드가 있었습니다. (ex. <3, 4, 1>, <3, 4, 2>)

for(int i=0; i<m; i++){
	int st, en, v;
	cin >> st >> en >> v;
	a[st][en] = min(a[st][en], v);
}

이때는 최단 거리를 구하는 것이기 때문에 입력 받을 때 더 최소인 값으로 업데이트면서 다음 입력값을 받으면 됩니다.

다음으로 1~5번 노드를 하나씩 중간노드로 설정하면서 최단 거리를 업데이트 해주면 됩니다.

1번 노드가 중간 노드일 때

노드 번호	1	2	3	4	5
1	0	2	3	1	10
2	INF	0	INF	2	INF
3	8	10	0	1	1
4	INF	INF	INF	0	3
5	7	4	10	8	0

3 -> 1 -> 2 : 8 + 2 = 10
5 -> 1 -> 3 : 7 + 3 = 10
5 -> 1 -> 4 : 7 + 1 = 8

2번 노드가 중간 노드일 때

노드 번호	1	2	3	4	5
1	0	2	3	1	10
2	INF	0	INF	2	INF
3	8	10	0	1	1
4	INF	INF	INF	0	3
5	7	4	10	6	0

5 -> 2 -> 4 : 4 + 2 = 6
이 때 5 -> 1 -> 4 경로로 갔을 때 8 이었지만 2번 노드를 통해서 구한 최단 경로를 6으로 업데이트 해줍니다.

이러한 과정을 통해서 2~5번 까지 중간 노드를 두어 다 확인하게 되면

최종적으로

노드 번호	1	2	3	4	5
1	0	2	3	1	4
2	12	0	15	2	5
3	8	5	0	1	1
4	10	7	13	0	3
5	7	4	10	6	0

이 되게 됩니다.

💻전체 코드

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

int n,m;
int a[104][104];
const int INF = 1e9;
int main(void){
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> m;
	
	for(int i=0; i<=n; i++){
		for(int j=0; j<=n; j++){
			if(i == j) a[i][j] = 0;
			else a[i][j] = INF;
		}
	}
	
	for(int i=0; i<m; i++){
		int st, en, v;
		cin >> st >> en >> v;
		a[st][en] = min(a[st][en], v);
	}
	
	for(int k=1; k<=n; k++){
		for(int i=1; i<=n; i++){
			for(int j=1; j<=n; j++){
				a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
			}
		}
	}
	
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			if(a[i][j] == INF) cout << "0 ";
			else cout << a[i][j] << ' ';
		}
		cout << '\n';
	}
	
	return 0;
}