❓문제 설명

문제 : 백준 15565 귀여운 라이언

난이도 : 실버 1

문제 요약
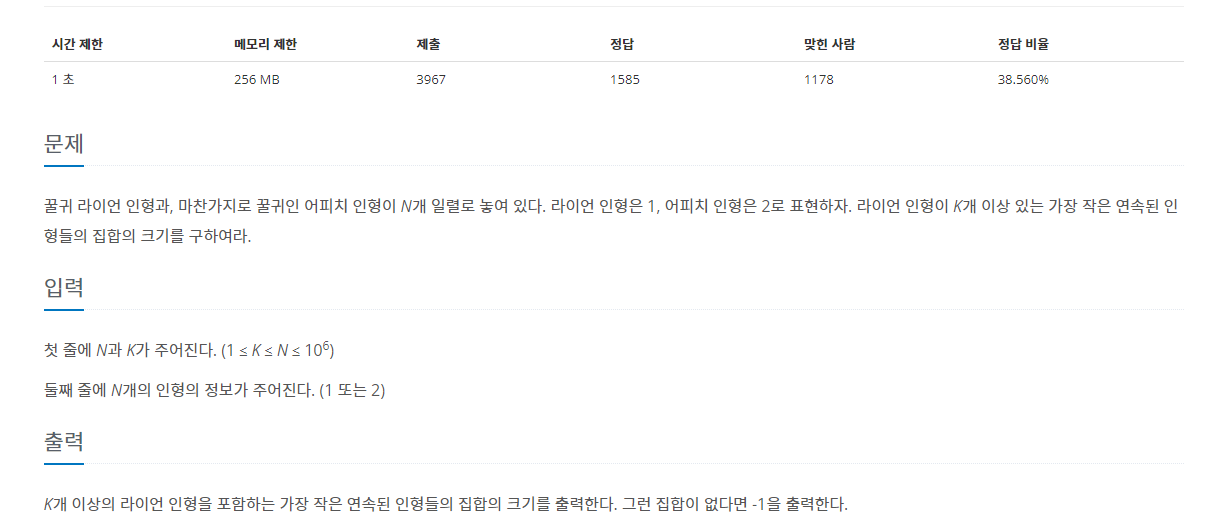
1. 꿀귀 라이언 인형과 꿀귀 어피치 인형이 N개 일렬로 놓여 있습니다.
2. 라이언 인형은 1, 어피치 인형은 2로 표현됩니다.
3. 라이언 인형이 K개 이상 있는 가장 작은 연속된 인형들의 집합의 크기를 구하는 문제 입니다.

n, k (1 <= k <= n <= 100만)

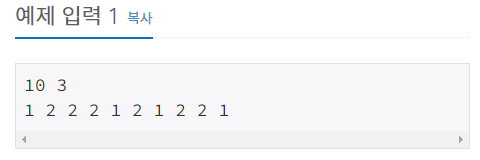
N이 10, K가 3

예제로 주어진 인형 배열을 그림으로 표현하면 아래와 같습니다.

라이언 인형이 K개 이상 있는 집합이 하나라도 존재해야지 이 문제에 답이 존재하기에 먼저 라이언이 K개 이상인지 입력받으면서 확인합니다.

for(int i=1; i<=n; i++){
	int x;
	cin >> x;
	if(x == 1){
		v.push_back(i);
	}
}

if(v.size() < k){
	cout << -1;
	return 0;
}

라이언(1)이 들어오면 벡터에 넣어주고 벡터의 크기가 K 보다 작으면 -1을 출력하고 종료하게 됩니다.

예시에서는 K가 3으로 주어졌으므로

라이언이 3개 이상일 경우를 살펴보겠습니다.

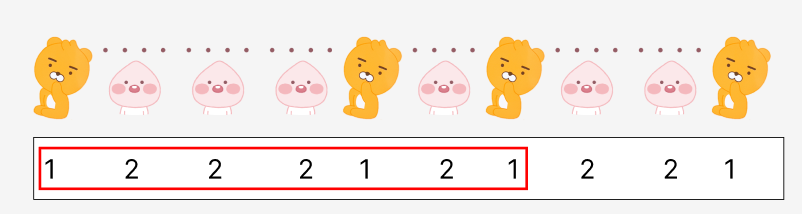
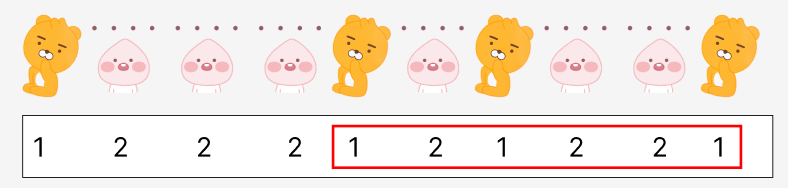
라이언 인형을 딱 3개만 가지고 있는 집합은 두 가지가 있습니다.

첫 번째 집합의 크기는 7
두 번째 집합의 크기는 6

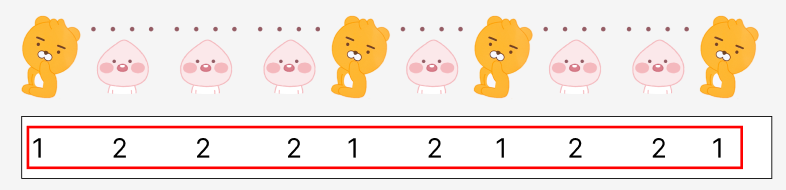
물론 K(3)개 이상인 4개를 가진 집합도 존재합니다. 하지만 저희는 최소가 되는 집합의 크기를 구해야하므로 K(3)개를 넘어가는 집합은 확인하지 않아도 됩니다. 그러므로 2가지 경우만 살펴보겠습니다.

🎯문제 해결 방법

이 문제는 라이언 K개 이상 존재하더라도 K개를 가지는 경우만을 골라 집합의 크기를 비교하면서 최소 집합의 크기를 구해야합니다. 이때 슬라이딩 윈도우 알고리즘이 사용됩니다.

먼저 라이언이 들어오는 경우에만 라이언의 위치를 벡터에 넣어줍니다.

for(int i=1; i<=n; i++){
	int x;
	cin >> x;
	if(x == 1){
		v.push_back(i);
	}
}

그런 다음 벡터 안에서 K(3)개 만큼씩 확인합니다.

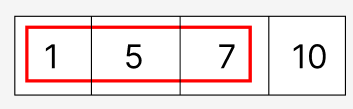
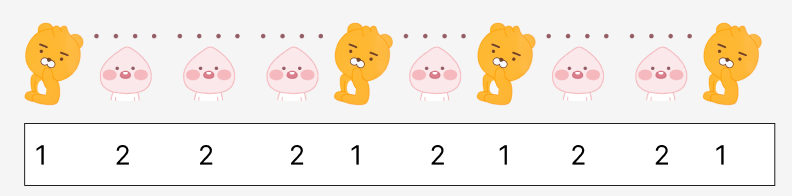
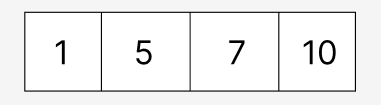
라이언의 위치들이므로 첫 번째 요소가 집합의 시작 위치 마지막 요소가 집합의 끝 위치를 나타냅니다. 1에서 7까지는 라이언이 1,5,7에 위치하며 집합의 크기는 7(1,2,3,4,5,6,7)입니다.

다음 집합을 확인할 때는 확인하는 크기는 그대로 둔 채 빨간 네모의 위치를 한 칸만 오른쪽으로 이동한다고 생각하면 됩니다.

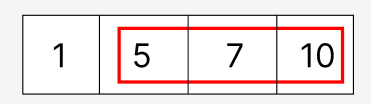
이 경우에는 라이언이 5,7,10에 위치하며 집합의 크기는 6(5,6,7,8,9,10)입니다.

그러므로 최종 답은 라이언이 3개일 때 가장 작은 집합의 크기인 6이 됩니다.

💻전체 코드

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

int n,k;
int a[1000004];
int ret = 1e9;
vector<int> v;
int main(void){
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> k;
	
	for(int i=1; i<=n; i++){
		int x;
		cin >> x;
		if(x == 1){
			v.push_back(i);
		}
	}
	
	if(v.size() < k){
		cout << -1;
		return 0;
	}
	int st=0,en=k-1;
	for(int i=0; i<=v.size()-k; i++){
		ret = min(ret, v[en] - v[st] + 1);
		en++;
		st++;
	}
	cout << ret;
	return 0;
}