
백준 1976 여행 가자 문제 링크
문제에서 주어진 주요 조건
- 도시가 N개 있고 임의의 두 도시 사이에 길이 있다.
- 중간에 다른 도시를 경유해서 여행을 할 수 있다.
- 같은 도시를 여러 번 방문하는 것도 가능하다.
여행 경로가 주어졌을 때 가능한 경로인지 여부를 확인하면 되는 문제입니다.

시간 제한은 2초로 주어졌고 약 2억 번의 연산까지는 가능하겠다고 생각을 했습니다.

먼저 ! 아래 글을 보기 전에 1분 동안 각자 어떻게 풀면 좋을까 생각해봅시다.
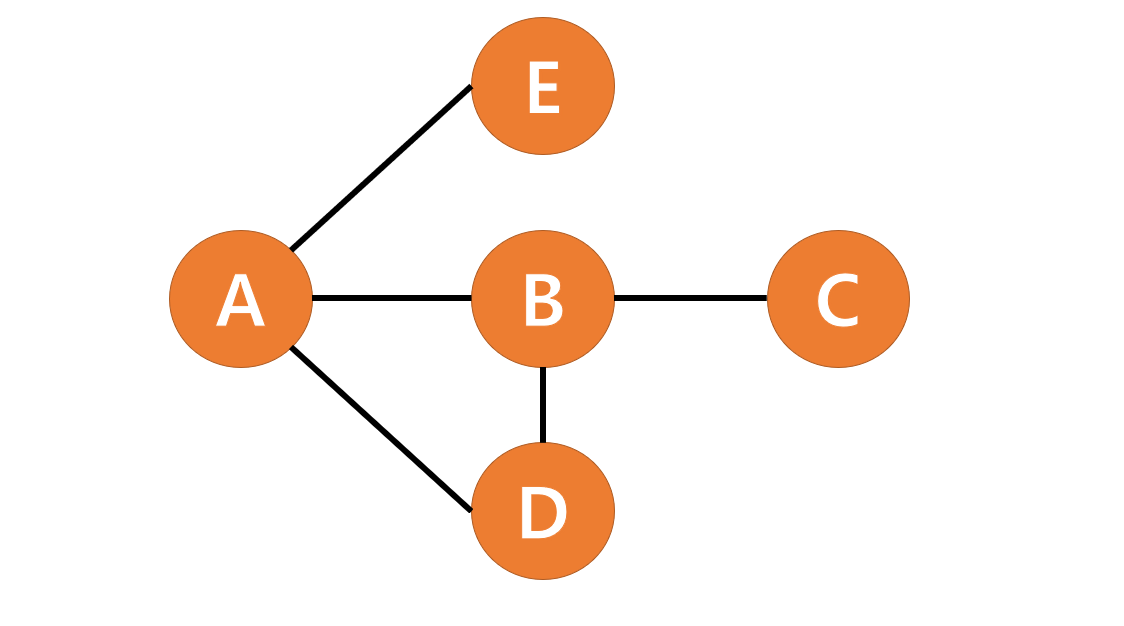
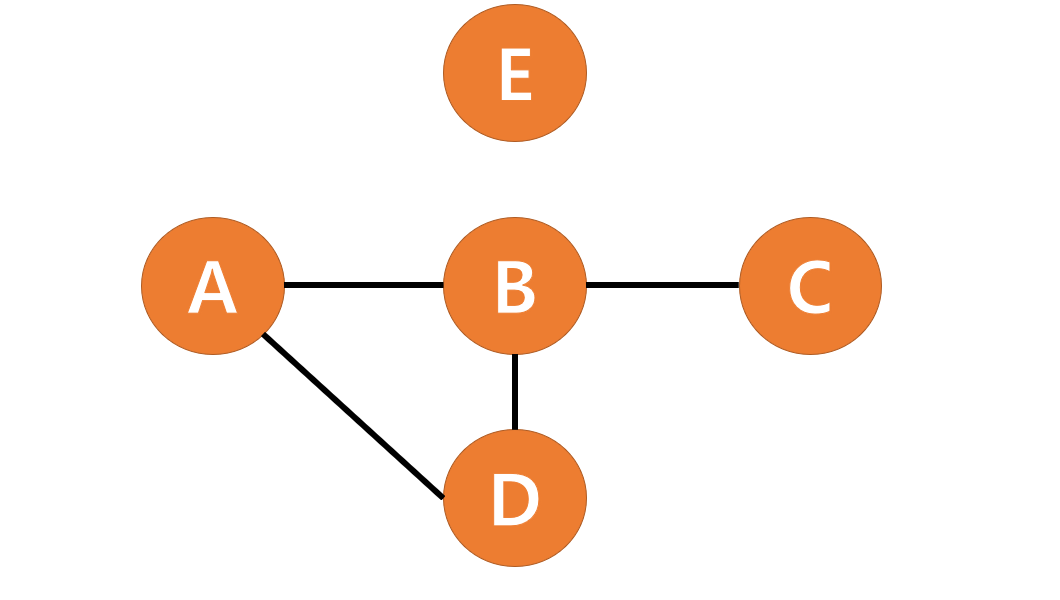
문제에서 주어진 5개의 도시 정보들을 그림으로 그린 모습입니다.
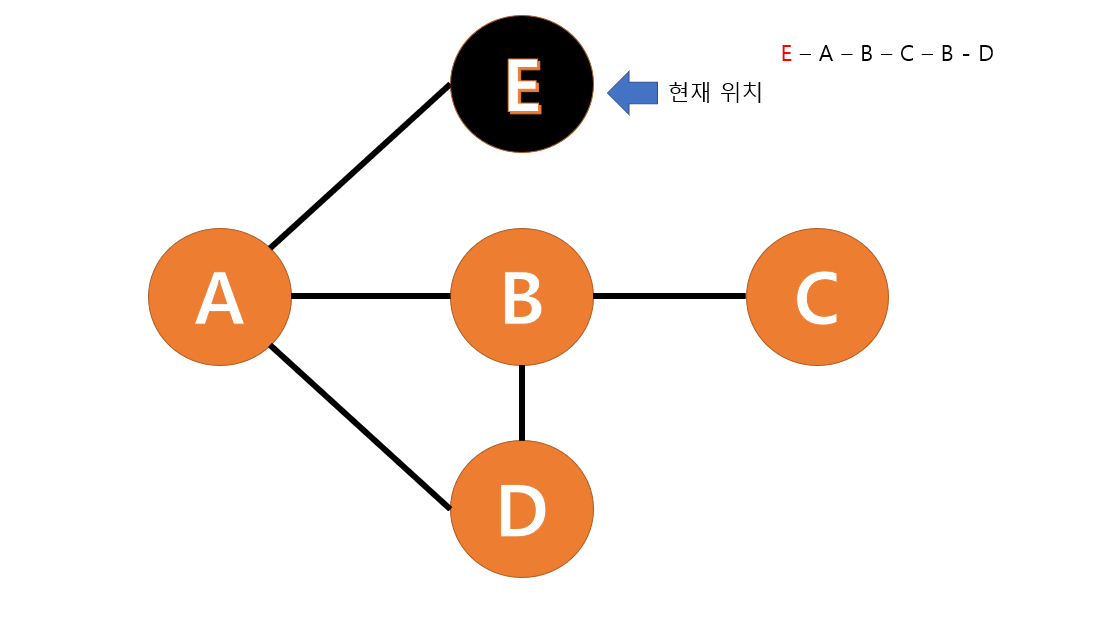
주어진 여행 경로는 E - A - B - C - B - D 순으로
먼저 E 를 방문합니다.
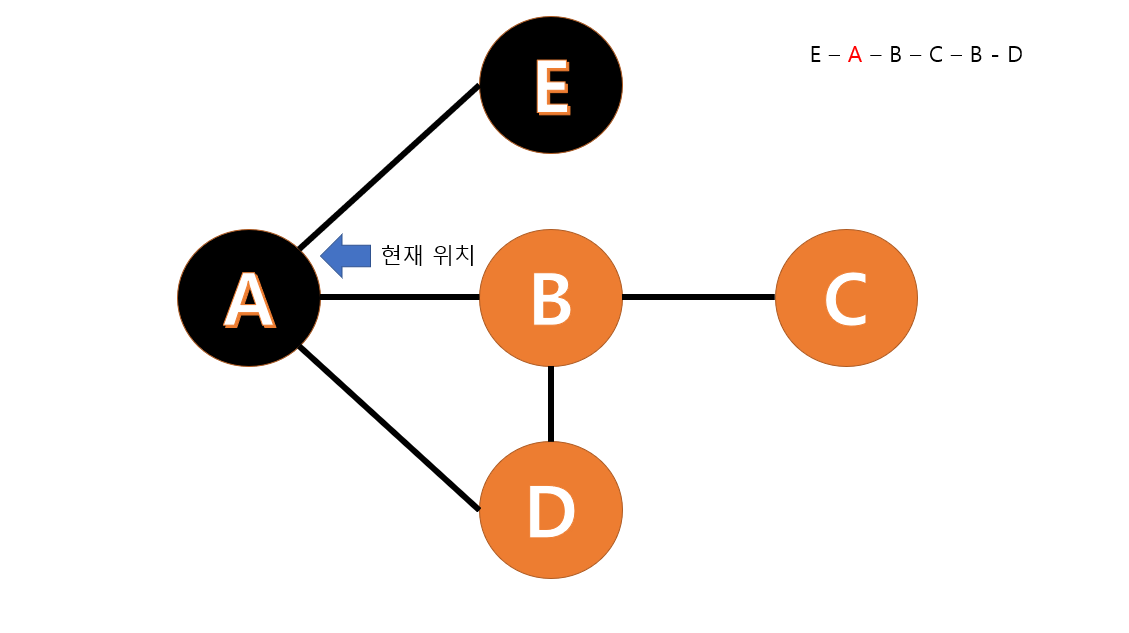
그 다음 E 와 A가 연결된 길을 따라 A 를 방문합니다.
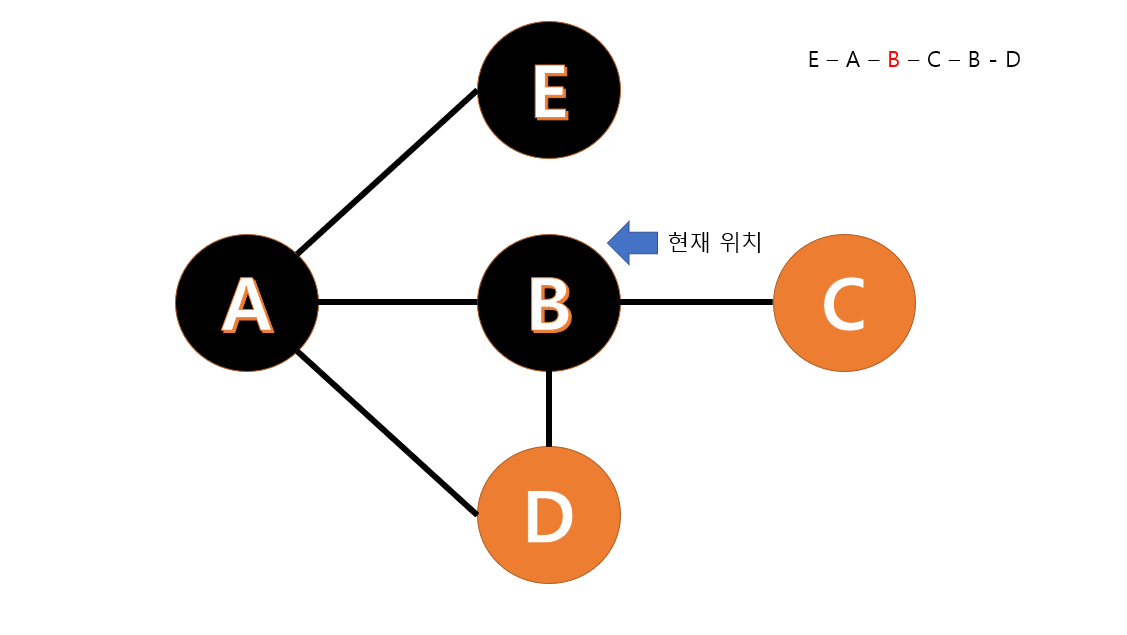
A 와 B가 연결된 길을 따라 B 를 방문합니다.
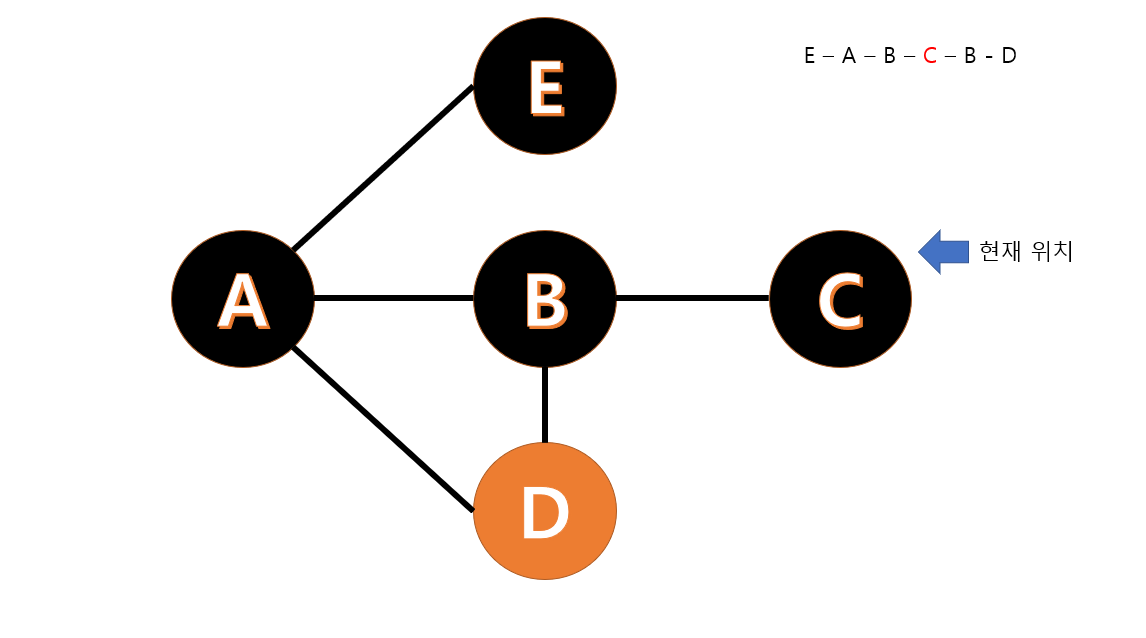
B 와 C 가 연결된 길을 따라 C 를 방문합니다.
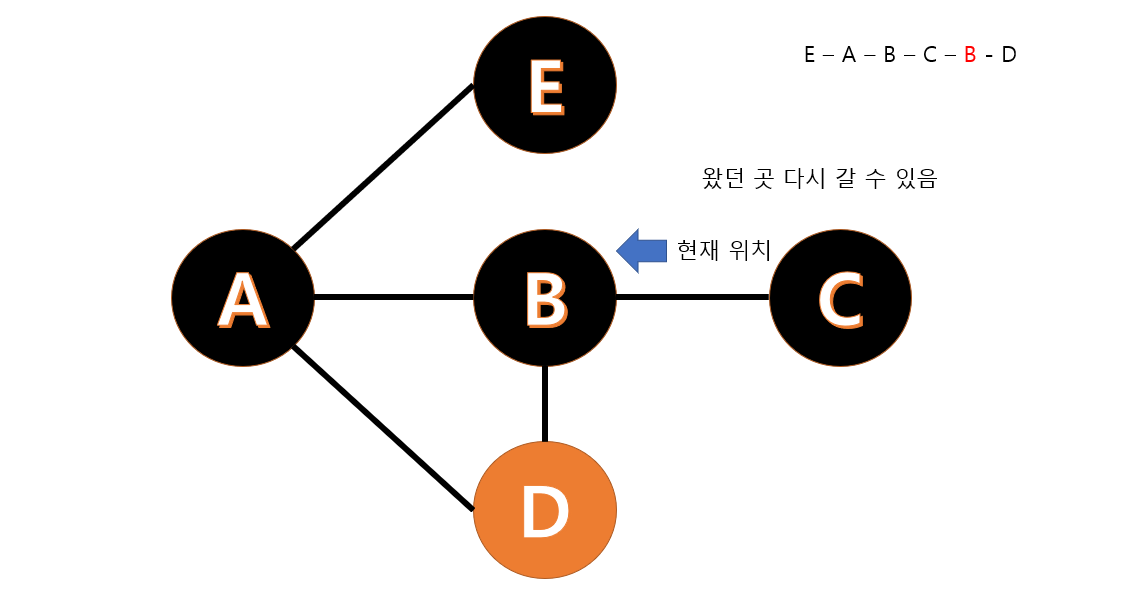
여행 일정에 따라 B 를 다시 방문해야합니다. 주어진 조건에서 같은 도시를 여러 번 방문하는 것이 가능하다고 했기 때문에 B 로 다시 갈 수 있습니다.
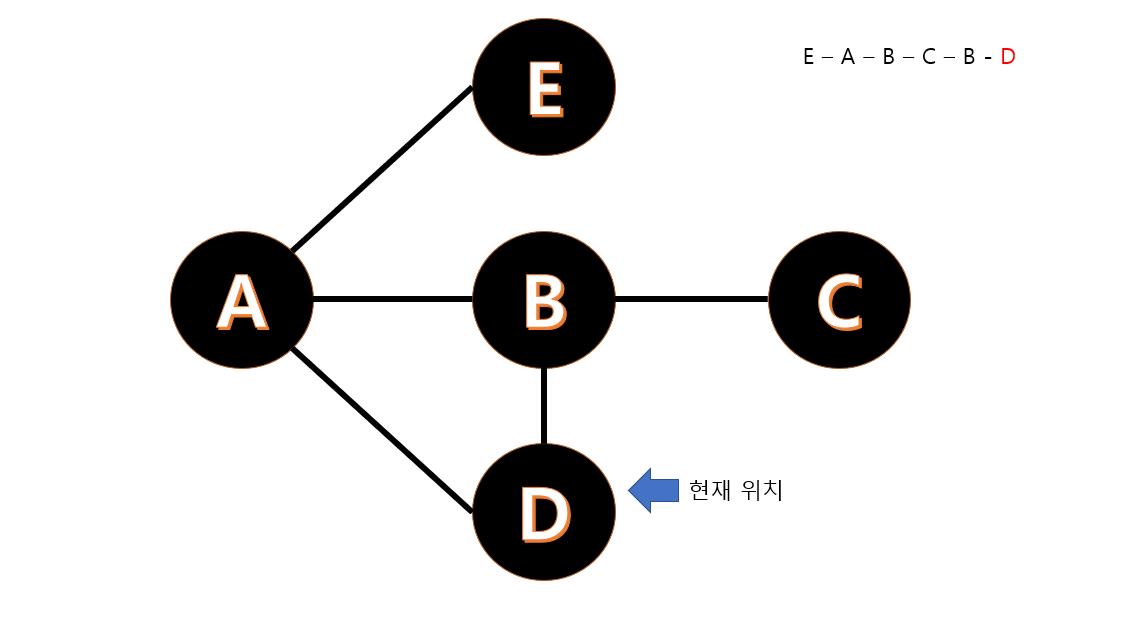
B 와 D 가 연결된 길을 따라 D 를 방문합니다.
이렇게 한 지역을 방문했을 때 연결된 길을 따라 주어진 여행 경로를 모두 방문 가능하다면 "YES" 를 출력하게됩니다.
다음으로 A 와 E 가 연결된 길이 없는 경우 입니다.
모든 지역이 길로 연결되어 있지 않은 모습이죠.
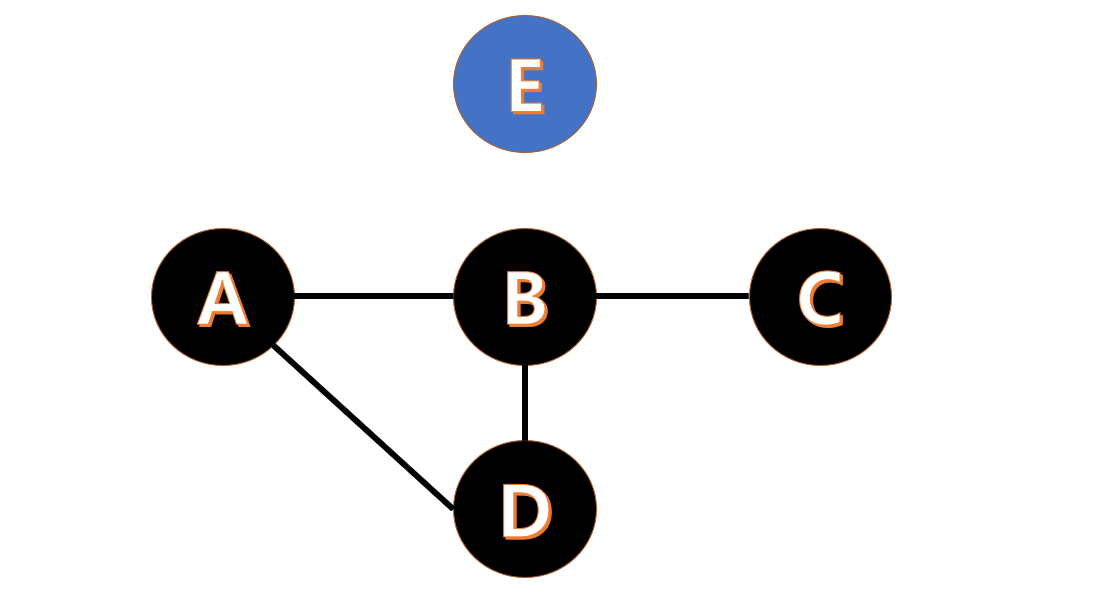
이런 경우에는 E 를 먼저 방문하고 다른 지역으로 이동할 수도 없고 A 를 먼저 방문해도 E 로 이동할 수 없습니다. 불가능한 여행경로로 판단하여 "NO"를 출력하게됩니다.

그래서 저는 이 문제는 모든 지역이 연결되어 있는지를 확인하는 문제이구나! 라고 생각했습니다.
모든 지역을 방문할 때는 DFS 알고리즘을 사용했습니다.

도시들의 정보를 입력받습니다.
시간복잡도: O(n^2)
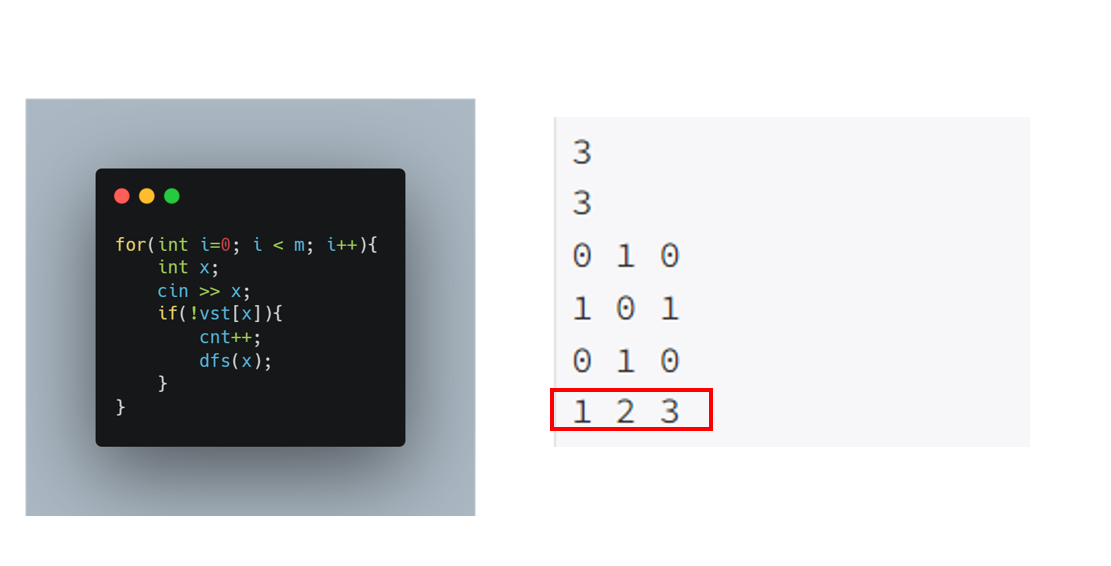
여행 경로 정보를 입력받습니다.
시간복잡도: O(m)

첫 번째 코드는 DFS 알고리즘 코드입니다. 연결된 지역들을 모두 탐색합니다.
두 번째 코드는 여행 경로를 입력 받을 때 처음으로 입력받은 지역 번호로 DFS 를 돌아 모든 지역이 접근돼서 더 이상 DFS를 호출하지 않으면 cnt 값을 1이 됩니다. 만약 모든 지역을 방문하지 못하면 DFS를 또 호출하게 되므로 cnt 값이 증가하게 되어 1이 아니게 됩니다.
즉, cnt 값이 1이면 모든 지역을 방문했다고 판단하고 "YES"를 출력합니다.
반대로 1이 아니라면 "NO"를 출력합니다.
코드
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<stack>
#include<queue>
#include<vector>
using namespace std;
int n,m,cnt;
vector<int> v[204];
bool vst[204];
void dfs(int k){
vst[k] = 1;
for(int e: v[k]){
if(!vst[e]){
dfs(e);
}
}
return;
}
int main(void) {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
int x;
cin >> x;
if(x == 1) {
v[i].push_back(j);
}
}
}
for(int i=0; i < m; i++){
int x;
cin >> x;
if(!vst[x]){
cnt++;
dfs(x);
}
}
if(cnt == 1) cout << "YES";
else cout << "NO";
return 0;
}다른 사람들은 어떻게 풀었을까?
왜 이 문제가 분리 집합 문제로 분류가 되어있을까??
DFS, BFS 쪽으로 분류되는게 맞겠는데... 생각하고 다른 분들의 코드를 봤습니다.

확인해보니 많은 사람들이 이 문제를 Union Find 알고리즘을 사용해서 푼 것을 확인했습니다.
Union Find 알고리즘까지 간단하게 알아보고 이 문제를 제대로 부셔봅시다..
Union Find 알고리즘이란?
Disjoint Set : 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조입니다.
즉, Disjoint Set = 서로소 집합 자료구조 라고 할 수 있습니다.
이러한 Disjoint Set 을 표현할 때 사용하는 알고리즘이 Union Find 알고리즘입니다.
Union Find 연산
- make-set(x) : x 를 유일한 원소로 하는 새로운 집합을 만듭니다.
- union(x, y) : x 가 속한 집합과 y 가 속한 집합을 합칩니다.
- find(x) : x 가 속한 집합의 루트 노드 값을 반환합니다.
make-set
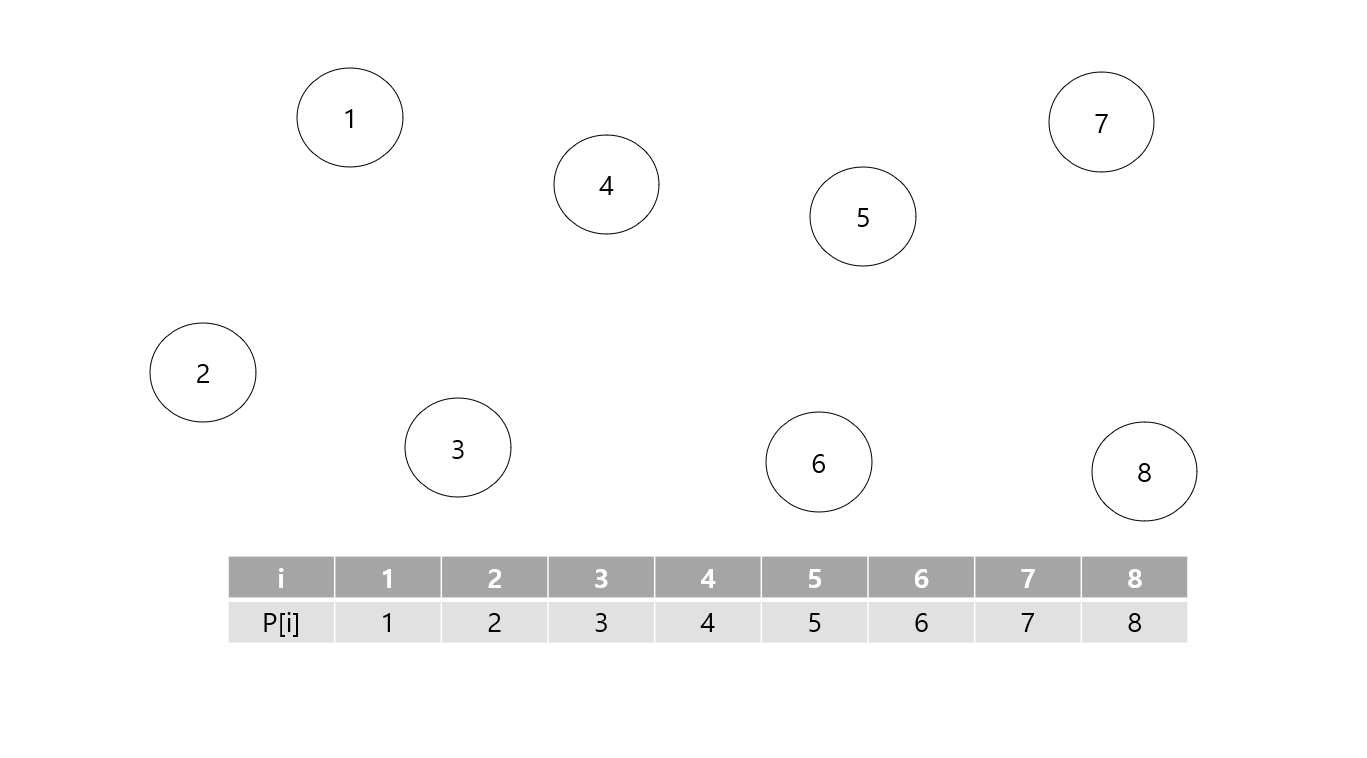
각 노드의 루트 노드가 자기 자신을 가리키도록 초기화 해줍니다.
Union
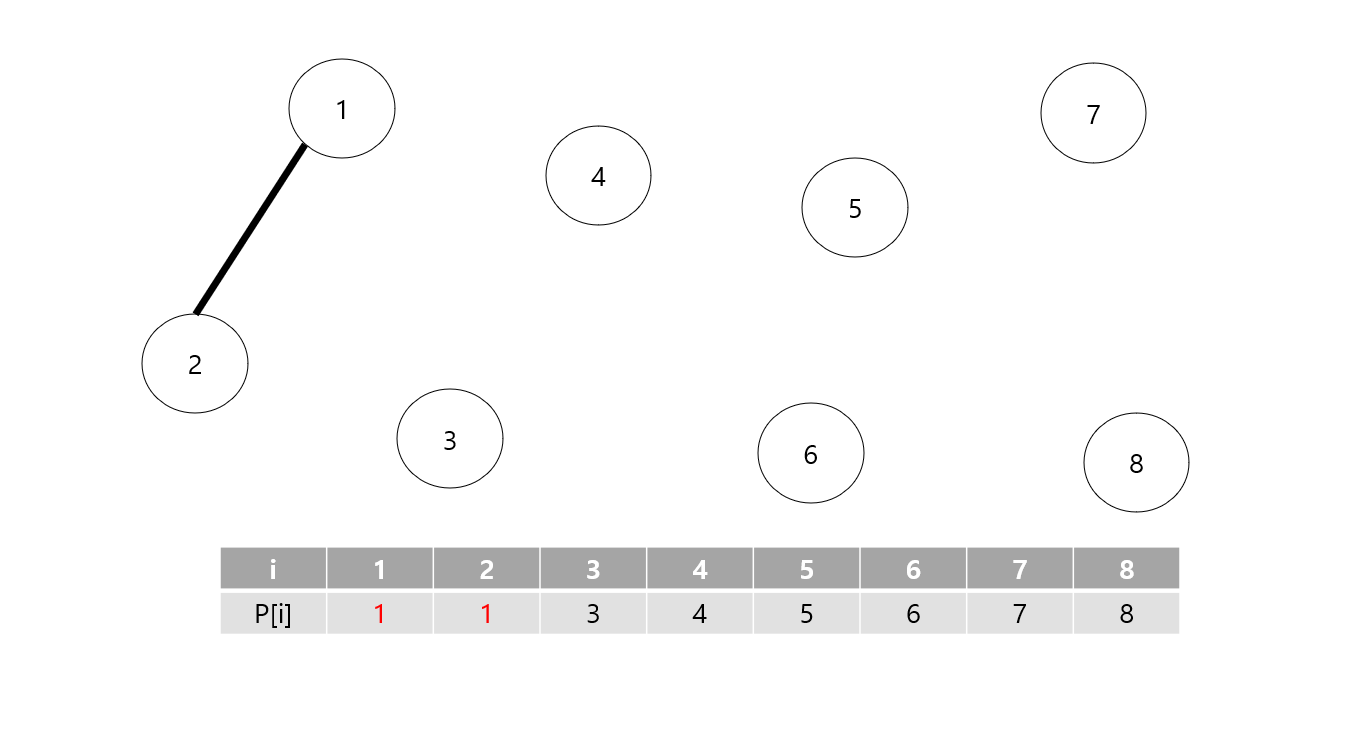
두 노드가 연결되는 Union 연산을 할 때는 더 작은 값을 집합의 부모 노드로 설정하는 것이 일반적이므로 여기서는 가장 작은 노드의 값이 루트 노드가 되는 방식으로 설명하겠습니다.
1번 노드와 2번 노드가 합쳐지면서 더 작은 값인 1번 노드가 2번 노드의 부모 노드가 1이라고 값을 변경해줍니다.
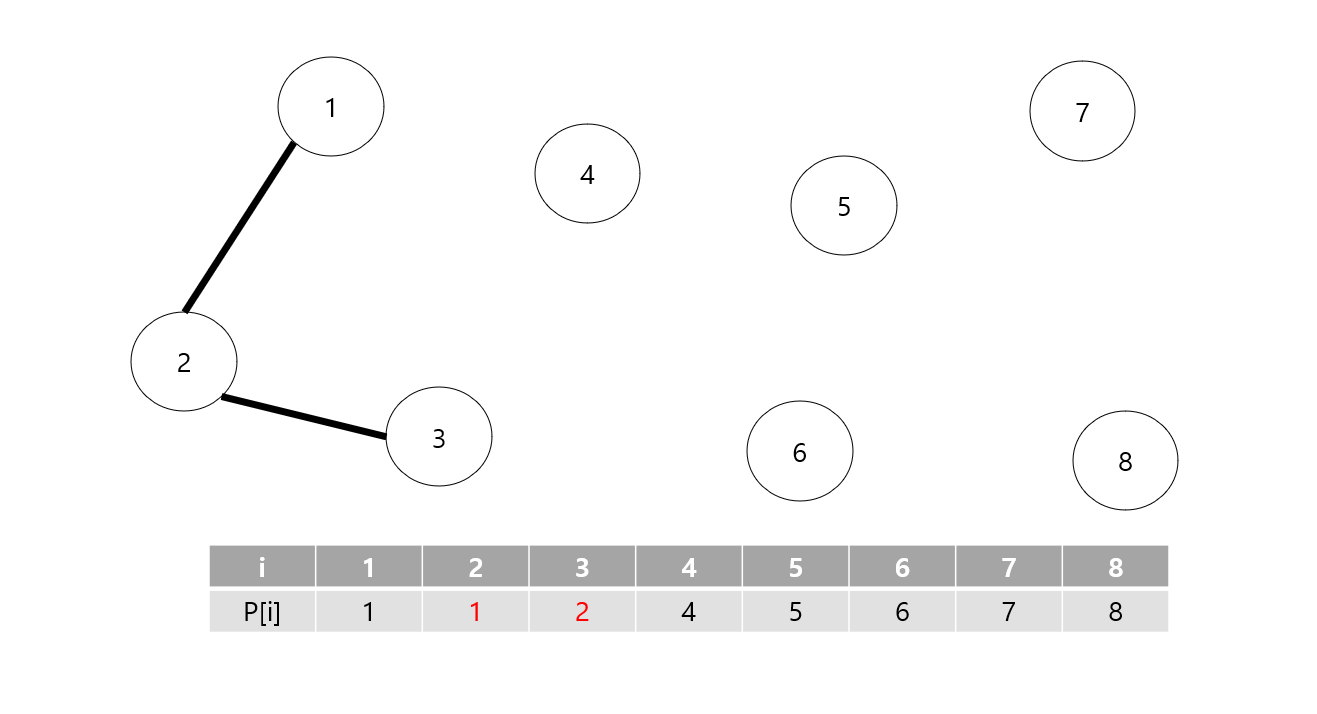
여기서는 2번 노드와 3번 노드가 합쳐지면서 더 작은 값인 2번 노드가 3번 노드의 부모라고 값을 변경해줍니다.
이렇게 부모 노드로만 값을 변경해주면 딱 봤을 때 같은 집합인지 알아내기가 어렵습니다.
Find
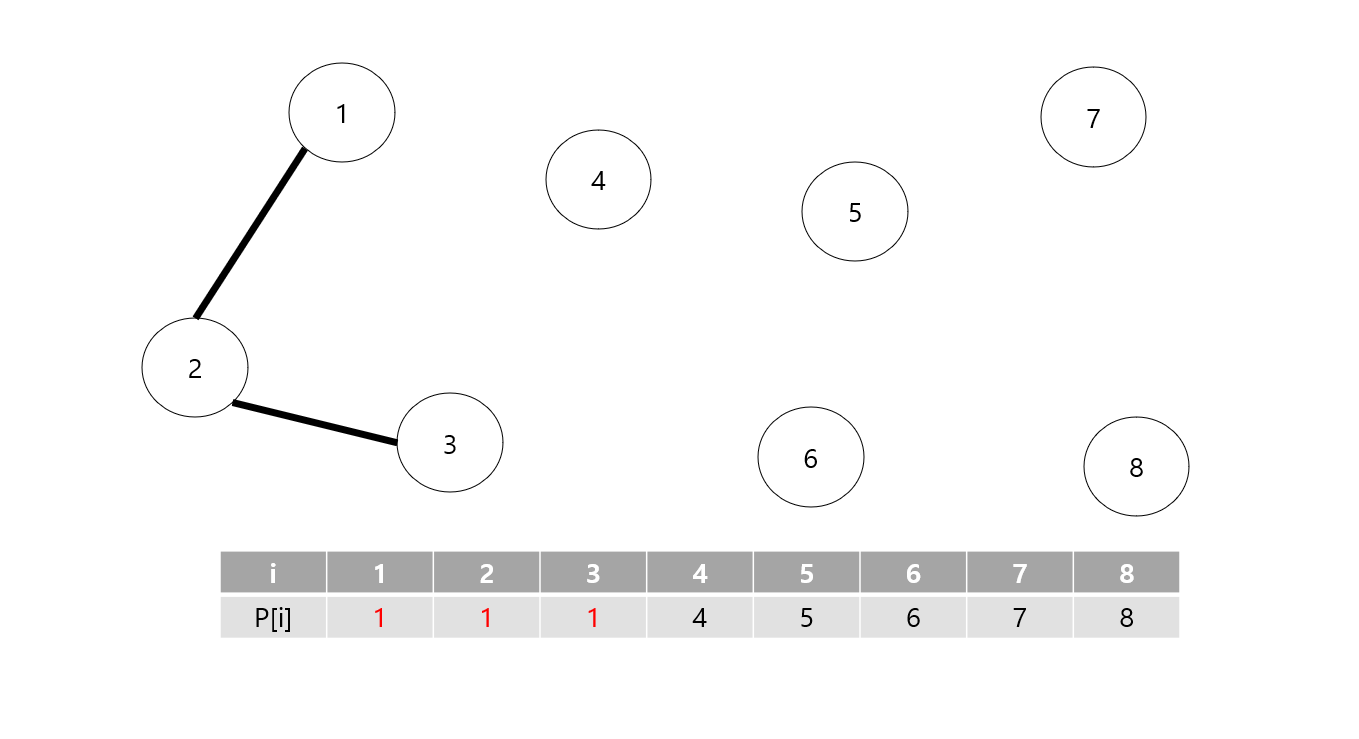
그래서 "재귀"를 통해 3번 노드의 부모 노드는 2번 노드이고 2번 노드의 부모 노드는 1번 노드임을 알아내서 이 집합의 루트 노드는 1번 노드이구나! 라고 알 수 있게 됩니다.
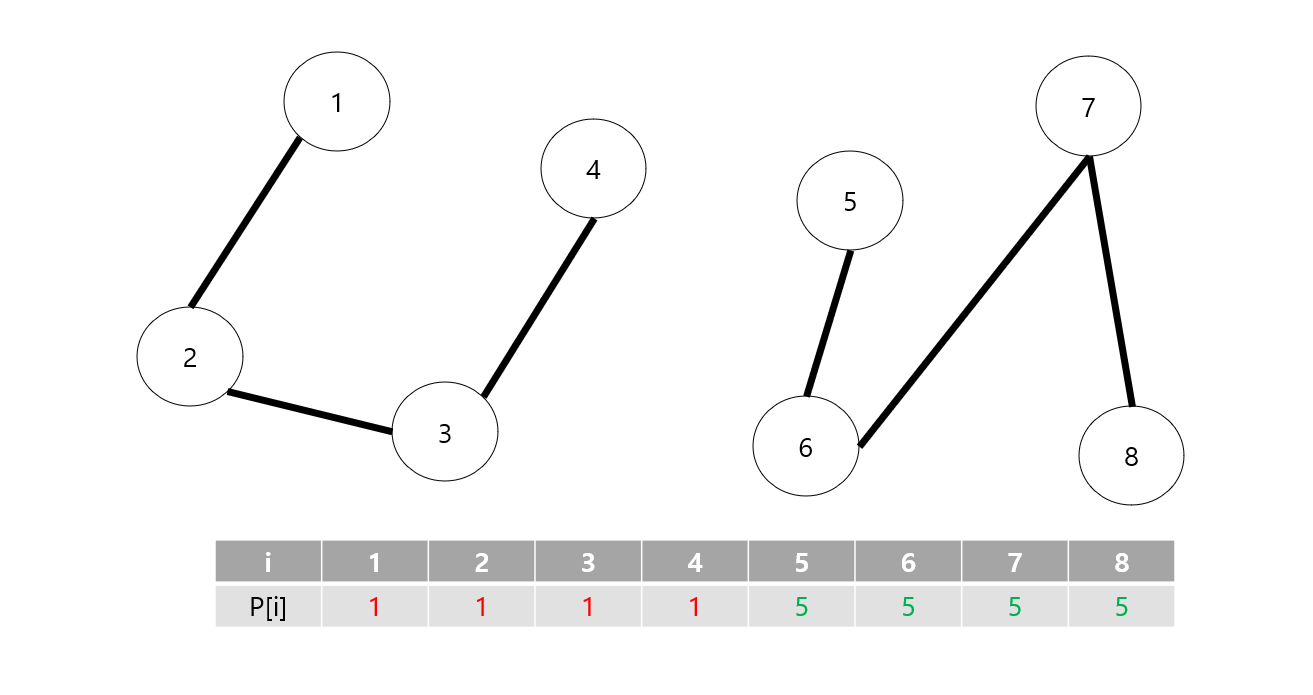
위 그림처럼 노드들이 연결되면 P[i] 의 값은 표와 같게 됩니다.
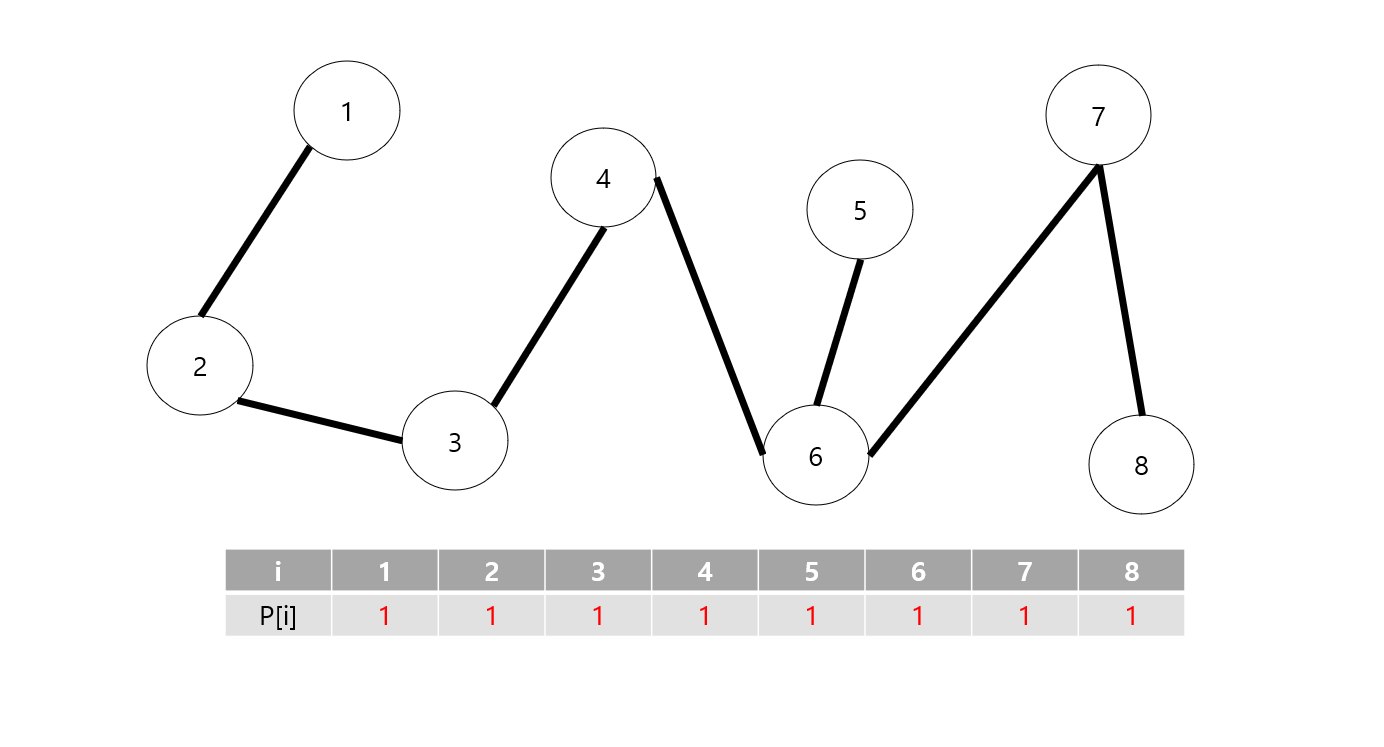
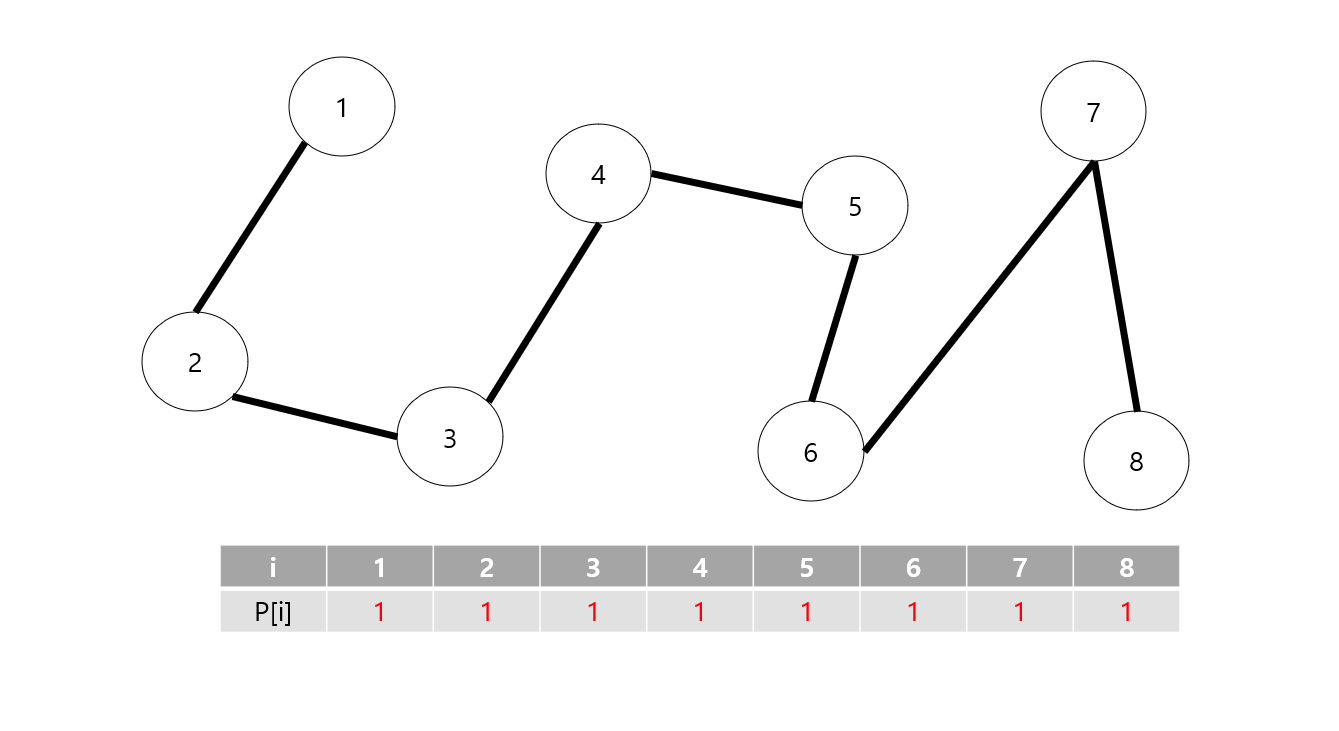
4번 노드와 6번 노드와 연결되거나 4번 노드와 5번 노드와 연결되는 것과 같이 다른 집합의 노드끼리 Union 연산이 이루어지면 같은 집합으로 여겨지고 P[i] 에는 루트 노드의 값이 들어가게 되어 같은 집합임을 알 수 있습니다.
Union Find 로 푼 코드
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<stack>
#include<queue>
#include<vector>
using namespace std;
int n,m,cnt;
int p[201];
int find(int x){
if(p[x] == x) return x;
return p[x] = find(p[x]);
}
void union_node(int x, int y){
x = find(x);
y = find(y);
if(x < y) p[y] = x;
else p[x] = y;
}
int main(void) {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i=1; i<=n; i++) p[i] = i;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
int x;
cin >> x;
if(x == 1) {
union_node(i,j);
}
}
}
int root;
for(int i=0; i<m; i++){
int x;
cin >> x;
if(i == 0) root = find(x);
else{
if(find(root) != find(x)){
cout << "NO";
return 0;
}
}
}
cout << "YES";
return 0;
}