백준 1285 C++ 동전 뒤집기

DoooongDong·2023년 1월 3일

cpp 비트마스킹 완전탐색

골드를 풀면서 300년, 모르는 사이에 레벨 MAX가 되었습니다

목록 보기

2/28

❓ 문제 설명

백준 1285 동전 뒤집기 풀러가기

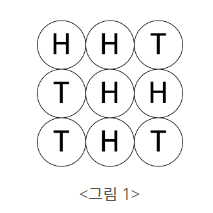
앞면 : H, 뒷면 : T
N^2개의 동전에 대하여 임의의 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업을 수행할 수 있습니다.

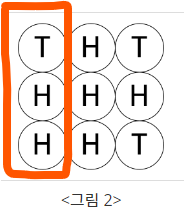
<그림 1>의 상태에서 첫 번째 열에 놓인 동전을 모두 뒤집으면 <그림 2>와 같습니다.

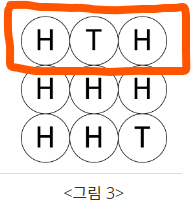
<그림 2>의 상태에서 첫 번째 행에 놓인 동전을 모두 뒤집으면 <그림 3>과 같습니다.

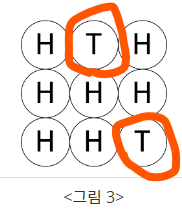
<그림 3>의 상태에서 뒷면(T)이 위를 향하여 놓인 동전의 개수는 두 개입니다.
이 예시에서는 어떻게 계속 뒤집든 간에 뒷면이 나오는 동전의 개수를 2개보다 작게 만들 수 없습니다.

이 문제에서 물어보는건 무엇인가?!

N^2개의 동전들의 초기 상태가 주어질 때, 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업들을 수행하여 뒷면이 위를 향하는 동전 개수를 최소로 하려한다. 이때의 최소 개수를 구하는 프로그램을 작성하시오.

1. 입력

첫째 줄에 20이하의 자연수 N이 주어진다. 둘째 줄부터 N줄에 걸쳐 N개씩 동전들의 초기 상태가 주어진다. 각 줄에는 한 행에 놓인 N개의 동전의 상태가 왼쪽부터 차례대로 주어지는데, 앞면이 위를 향하도록 놓인 경우 H, 뒷면이 위를 향하도록 놓인 경우 T로 표시되며 이들 사이에 공백은 없다.

2. 출력

첫째 줄에 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업들을 수행하여 뒷면이 위를 향하여 놓일 수 있는 동전의 최소 개수를 출력한다.

🛠️ 문제 풀이

시간 제한은 6초입니다.
뒤집는 순서에 따라서도 답이 변하기 때문에 모든 경우의 수를 다 확인해야하는 완전탐색 문제입니다.
N은 20이하의 수로 굉장히 적지만 행과 열이 각각 20일때 모든 경우의 수는 2^40으로 굉장히 커지게 됩니다.
그래서 무작정 모든 경우의 수를 확인해서 풀게되면 시간초과가 발생하므로 다른 방법을 생각해야합니다.

1. 각 행의 뒤집기 여부를 먼저 확인한다.

N이 20일 때 행에 대해서만 먼저 뒤집는 경우와 안뒤집는 경우를 확인하는 경우의 수는 2^20으로 절반으로 줄어들게 됩니다.

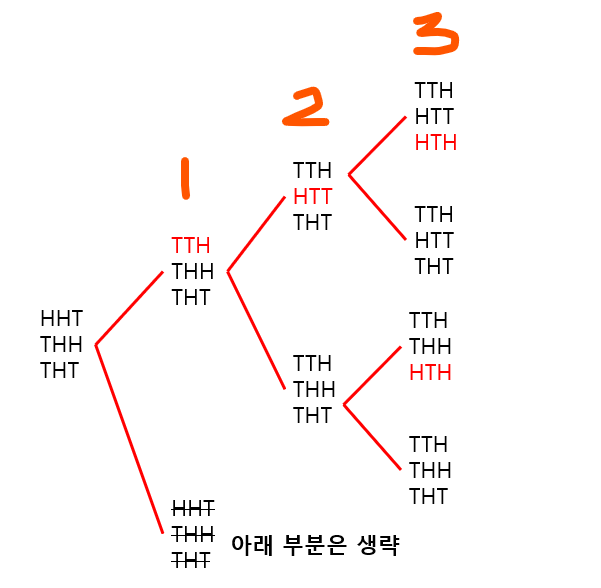
그림의 예시는 문제에서 주어진 예제로 그렸습니다.

빨간색 부분은 뒤집은 행을 의미합니다.

2. 각 열의 뒤집기 여부를 확인한다.

앞에서 구한 각 행에 대해서만 뒤집거나 안뒤집은 모든 경우에서 각 열을 뒤집어야하나 안뒤집어야하나 결정합니다.

이 문제에서 주어진 예시에서 정답이 되는 경우를 살펴보겠습니다.

첫 번째 열을 확인합니다. TTT 뒷면이 3개이므로 뒤집는 경우 HHH 로 뒷면이 0개로 최소가 됩니다. 그러므로 첫 번째 열은 뒤집습니다.

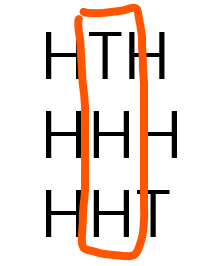
두 번째 열을 확인합니다. THH 뒷면이 1개입니다. 뒤집을 경우 HTT 로 뒷면이 2개로 더 많아지므로 뒤집지 않습니다.

세 번째 열을 확인합니다. HHT 뒷면이 1개입니다. 뒤집을 경우 TTH 로 뒷면이 2개로 더 많아지므로 뒤집지 않습니다.

이런식으로 그리디하게 저희가 구하고자하는 뒷면이 최소가 되는 경우를 찾을 수 있게됩니다.

🔧 비트마스킹을 이용해서 완전탐색을 해결하자

비트 마스킹에 대해 정리했어요 😊

for(int i=1; i<=n; i++){
	cin >> s;
	int v = 1;
	for(int j=0; j<s.size(); j++){
		if(s[j] == 'T') a[i] |= v;
		v *= 2;
	}
}

뒷면인 경우 1, 앞면인 경우 0
a[n] 배열에 각 행별로 뒷면이 나온 부분에 대해서 해당 비트를 1로 만듭니다.
이해를 돕기위해 THT 인 경우 이진수로 표현하면 101 이 됩니다.
이진수 101은 십진수로 5이므로 해당 a 배열에는 THT의 정보를 담을 때 5가 저장됩니다.
나중에 이 값을 봤을 때 5 == 101(2) 임을 이용해서 이 행의 첫번째와 세번째 동전이 뒷면임을 알 수 있습니다.

a[cur] = ~a[cur]; //cur행 뒤집기
func(cur + 1);
a[cur] = ~a[cur]; //cur행 뒤집었던거 다시 뒤집음 (그대로 진행)
func(cur + 1);

위에서 행을 뒤집는 경우와 안뒤집는 경우에 대해서 그림으로 설명한 부분이 있습니다.
그 부분을 코드로 작성한 부분입니다.

if(cur == n + 1){	
	int sum = 0;
	for(int i=1; i<= 1 << (n-1); i*=2){
		int cnt = 0;
		for(int j=1; j<=n; j++){
			if(a[j] & i) cnt++; //
		}
		sum += min(cnt, n - cnt);
	}
	ret = min(ret, sum);
	return;
}

n행까지 모두 다 뒤집은 경우 cur의 값은 n+1이 됩니다. 이때를 재귀를 탈출하는 base condition으로 설정해줍니다.
2중 for문 안에서는 j(각 행)에 대해서 i번째 비트가 1인지(뒷면)를 확인합니다.
뒷면의 개수(cnt)와 안뒤집은 뒷면의 개수(n - cnt) 둘을 비교해서 최소인 값으로 모든 뒷면의 수를 담는 sum에 더해줍니다.

🔧 시간복잡도

첫 번째 방법 시간복잡도 : O(2^(N+N)) -> N이 20일때 약 1조번의 연산으로 시간초과
두 번째 방법 시간복잡도 : O(2^N * N^2) -> N이 20일때 약 4억번의 연산으로 6초 통과

O(2^n) : 각 행의 뒤집기 여부 경우의 수 구하기
O(N^2) : 행 뒤집기 여부 끝난 각 열에 대해 뒷면의 개수 확인 후 최소가 되는 경우 구하기

💻 전체 코드

#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
#include<cstring>
using namespace std;
const int INF = 1e9;
int n;
int ret = INF;
int a[24];
string s;

void func(int cur){
	if(cur == n + 1){	
		int sum = 0;
		for(int i=1; i<= 1 << (n-1); i*=2){
			int cnt = 0;
			for(int j=1; j<=n; j++){
				if(a[j] & i) cnt++; //
			}
			sum += min(cnt, n - cnt);
		}
		ret = min(ret, sum);
		return;
	}
	
	a[cur] = ~a[cur]; //cur행 뒤집기
	func(cur + 1);
	a[cur] = ~a[cur]; //cur행 뒤집었던거 다시 뒤집음 (그대로 진행)
	func(cur + 1);
}

int main(void){
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n;
	for(int i=1; i<=n; i++){
		cin >> s;
		int v = 1;
		for(int j=0; j<s.size(); j++){
			if(s[j] == 'T') a[i] |= v;
			v *= 2;
		}
	}
	
	func(1);
	
	cout << ret;
	return 0;
}