❓문제 설명

문제: 2143 두 배열의 합

난이도: 골드 3

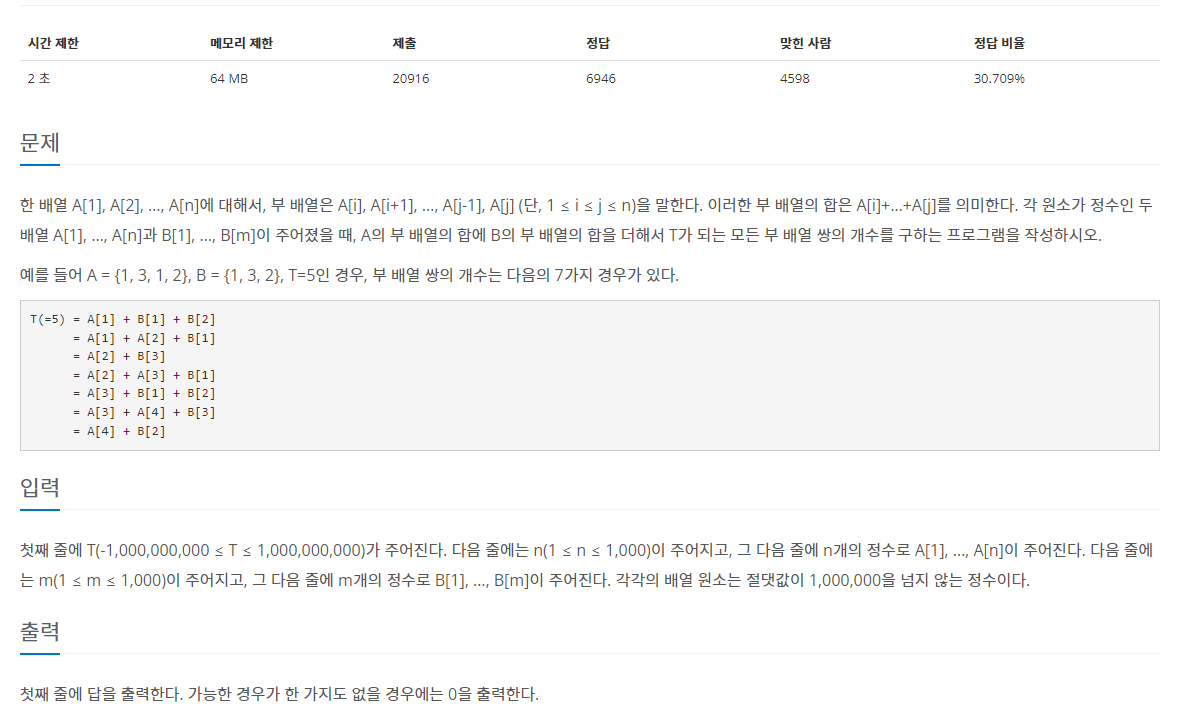
문제 요약

• 두 배열 A[1], …, A[n]과 B[1], …, B[m]이 주어집니다.
• 배열 A[1] ~ A[n]에 대해서, 부 배열은 A[i] ~ A[j] (단, 1 ≤ i ≤ j ≤ n)을 말합니다.
• 부 배열의 합은 A[i]+…+A[j]을 의미합니다.
• A의 부 배열의 합에 B의 부 배열의 합을 더해서 T가 되는 모든 부 배열 쌍의 개수를 구하면됩니다.

T가 5일 때 부 배열 쌍의 개수는 위 그림과 같습니다.

입력으로는 T(A, B 부 배열 합), n(A 배열 크기), m(B 배열 크기)가 주어집니다.

🎯문제 해결 방법

이 문제는 이분탐색으로 분류가 되어있지만 누적합으로도 분류가 되어있는 문제입니다.

ll t, n, m; 
ll x;
ll a[1004]; // a 배열
ll b[1004]; // b 배열
ll ret; // 모든 부 배열 쌍의 개수
unordered_map<ll,ll> um; // b 배열의 모든 부분합의 개수를 저장하기 위해 선언

사용할 변수들과 자료구조 입니다.

cin >> t;
cin >> n;
for(int i=1; i<=n; i++){
	cin >> x;
	a[i] = a[i-1] + x;
}
cin >> m;
for(int i=1; i<=m; i++){
	cin >> x;
	b[i] = b[i-1] + x;	
}

• t, n, m을 입력받고 a와 b 누적합을 구해둡니다.

for(int i=1; i<=m; i++){
	for(int j=i; j<=m; j++){
		um[b[j] - b[i-1]]++;
	}
}

• 이제 여기서 unordered_map에 b의 모든 부분합의 개수를 저장합니다!

for(int i=1; i<=n; i++){
	for(int j=i; j<=n; j++){
		ll tmp = t - (a[j] - a[i-1]);
		if(um[tmp] > 0) ret += um[tmp];
	}
}

• a의 모든 부분합을 확인하면서 t - (a의 부분합) == b의 부분합
  즉, a의 부분합 + b의 부분합 == t 임을 이용해서 unordered_map에 t - (a의 부분합) 에 해당되는 b의 부분합이 몇 개 있는지 확인하고 결과 값을 담는 ret 변수에 더해줍니다.

💻전체 코드

#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
ll t, n, m;
ll x; 
ll a[1004];
ll b[1004];
ll ret;
unordered_map<ll,ll> um;

int main(void){
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> t;
	cin >> n;
	for(int i=1; i<=n; i++){
		cin >> x;
		a[i] = a[i-1] + x;
	}
	cin >> m;
	for(int i=1; i<=m; i++){
		cin >> x;
		b[i] = b[i-1] + x;	
	}
	
	for(int i=1; i<=m; i++){
		for(int j=i; j<=m; j++){
			um[b[j] - b[i-1]]++;
		}
	}
	
	for(int i=1; i<=n; i++){
		for(int j=i; j<=n; j++){
			ll tmp = t - (a[j] - a[i-1]);
			if(um[tmp] > 0) ret += um[tmp];
		}
	}
	cout << ret;
	return 0;
}