❓문제 설명

문제 : 백준 2225번 합분해

난이도 : 골드 5

문제 요약

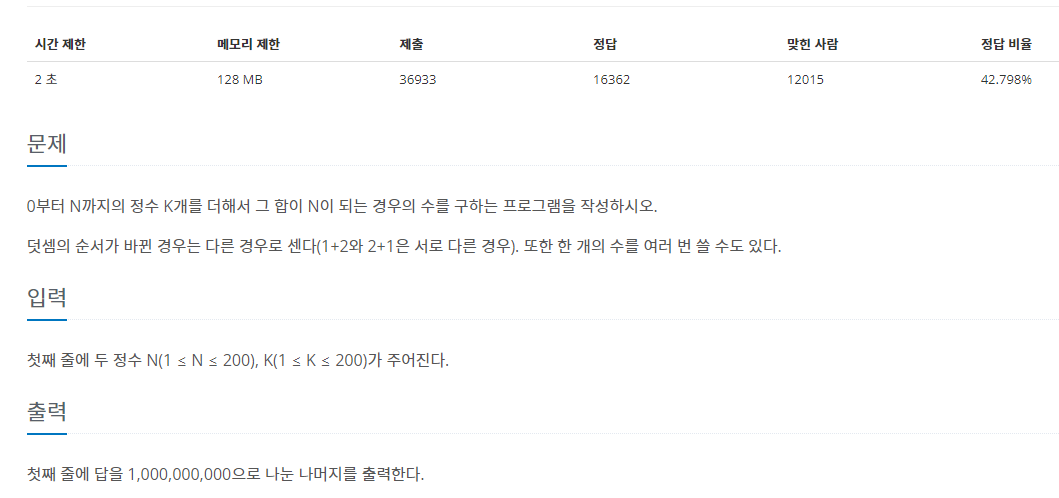
• 0부터 N까지 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하는 프로그램을 작성하시오.
• 1+2, 2+1은 서로 다른 경우로 모두 세어주어야 합니다.
• N(1이상 200이하), K(1이상 200이하)
• 답은 1,000,000,000으로 나눈 나머지를 출력합니다.

N이 20, K가 2인 예시로 설명하겠습니다.

정수 2개를 합쳐서 그 합이 20이 되는 경우는
0+20, 1+19, 2+18 ~~~ 19+1, 20+0 으로 총 21개입니다.

🎯문제 해결 방법

이 문제는 DP로 해결할 수 있습니다.
dp[K][N] = A : K개를 이용해서 N을 만들 수 있는 경우의 수가 A개이다.

DP 문제를 풀 때 규칙 즉, 점화식을 구해야합니다.

먼저, 어떠한 수 n을 만들기 위해서는 1개를 가지고도 만들 수 있음은 자명합니다. 예를 들어 1을 만들기 위해서는 1, 19를 만들기 위해서는 19 하나만 더해주면 되는 것이죠.

for(int i=0; i<=n; i++){
	dp[1][i] = 1
}

• 0부터 n까지 1개를 이용해서 만들 수 있는 경우의 수 1을 초기화 해줍니다.

그런 뒤에 dp[2][1]을 살펴보면 2개를 이용해서 1을 만들 수 있는 경우의 수를 구하면됩니다.
0+1, 1+0 으로 2가지 입니다.

지금 까지 알고 있는 정보는
dp[1][0] = 1, dp[1][1] = 1
dp[2][1] = 2
입니다.

다른 경우로 한번 더 살펴봅시다.
dp[2][2]의 값은 0+2, 2+0, 1+1으로 3가지 입니다.

저희가 알고있는 정보는
dp[1][0] = 1, dp[1][1] = 1, dp[1][2] = 1
dp[2][2] = 3
입니다.

여기서 규칙을 찾아보면
dp[k][n] = dp[k-1][0] + dp[k-1][1] + ... + dp[k-1][n] 임을 알 수 있습니다.

위에 식에 적용해보면 dp[2][2] = dp[1][0] + dp[1][1] + dp[1][2] 입니다.

for(int i=2; i<=k; i++){
	for(int j=0; j<=n; j++){
		for(int z=0; z<=j; z++){
			dp[i][j] += dp[i-1][z];
		}
		dp[i][j] %= m;
	}
}

위에 제가 말한 규칙을 코드로 작성하면 위와 같습니다. m은 1,000,000,000으로 답을 출력할 때 나머지를 구하기 위해 구한 경우의 수에 mod 연산을 해줍니다.

💻전체 코드

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll m = 1000000000;
ll n,k;
ll dp[204][204];
int main(void) {
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	
	cin >> n >> k;
	for(int i=0; i<=n; i++){
		dp[1][i] = 1;
	}
	for(int i=2; i<=k; i++){
		for(int j=0; j<=n; j++){
			for(int z=0; z<=j; z++){
				dp[i][j] += dp[i-1][z];
			}
			dp[i][j] %= m;
		}
	}
	cout << dp[k][n];
	return 0;
}