❓ 문제 설명

문제 : 백준 2473 세 용액
난이도 : 골드 3

문제 요약
1. 산성 용액의 특성값 1 ~ 10억, 알칼리성 용액의 특성값 -1 ~ -10억
2. 세 가지 용액을 혼합한 용액의 특성값은 각 용액의 합 입니다.
3. 이때 특성값이 0에 가까운 용액을 만들 때 사용된 세 용액의 특성값을 찾아 출력합니다.
4. N은 3 이상 5000 이하의 정수로 주어집니다.

예제

• 예제에서 5개의 용액의 특성값이 [-2, 6, -97, -6, 98]로 주어졌을 때 [-97, -2, 98]을 섞으면 -1 로 0에 가장 가까운 수를 만드므로 답이됩니다.

🎯 문제 해결 방법

• 이 문제는 앞 스터디에서 발표를 들었던 2470 두 용액 문제와 비슷합니다.

• 정렬된 배열에서 투 포인터 알고리즘을 이용하여 합이 0보다 작으면 start를 오른쪽으로 옮겨 큰 수를 가리키도록 하고 합이 0보다 크면 end를 왼쪽으로 옮겨 작은 수를 가리키도록 합니다.

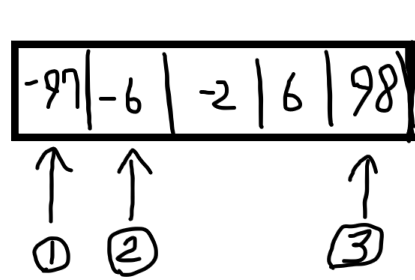
• 이 문제에서는 두 용액이 아닌 세 용액이므로 하나를 더 선택해줘야 합니다.

for(int i=1; i<=n-2; i++){
	ll st = i+1;
	ll en = n;
	while(st < en){
		...
	}
}

• 이 코드처럼 하나를 먼저 고정 시켜두고 start는 고정 시킨 다음 위치를 가리키고 end는 마지막 위치를 가리키도록 합니다.

• 이전에 풀었던 이분 탐색과 다르게 투 포인터를 이용한 문제에서는 'st <= en' 이 아니라 'st < en'을 사용했습니다. 그 이유는 st == en이 같아졌을 때는 3가지 용액을 모두 선택할 수 없는 경우의 수이기 때문입니다.

💻 전체 코드

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll; 
ll n;
ll a[5004];
ll ans[4];
//이 문제에서는 10억짜리 용액 3개가 합쳐진 30억을 최대로 잡고 풀어도 된다.
//문제 풀 때 이런 부분들은 빠르게 넘어갈 수 있도록 int의 최댓값 1e9, long long의 최댓값 1e18로 두고 넘어간다.
ll ret = 1e18; 

int main(void){
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n;
	for(int i=1; i<=n; i++){
		cin >> a[i];
	}
	sort(a+1, a+1+n);
	for(int i=1; i<=n-2; i++){
		ll st = i+1;
		ll en = n;
		while(st < en){
			ll v = a[i] + a[st] + a[en];
			if(abs(v) < ret){ //세 용액을 합쳤을 때 절대값이 이전에 구했던 합보다 0에 더 가까운지 확인한다.
				ret = abs(v); //ret을 갱신!
				ans[1] = a[i];
				ans[2] = a[st];
				ans[3] = a[en];
			}
			if(v < 0) st++; //합이 0보다 작을 경우 st를 오른쪽으로 한 칸 이동시킨다.
			else en--; //합이 0보다 크거나 같은 경우 en를 왼쪽으로 한 칸 이동시킨다.
		}
	}
	cout << ans[1] << ' ' << ans[2] << ' ' << ans[3];
	return 0;
}