
❓문제 설명
문제 : 백준 1937 욕심쟁이 판다 🐼
난이도 : 골드 3
✏️ 문제 요약
-
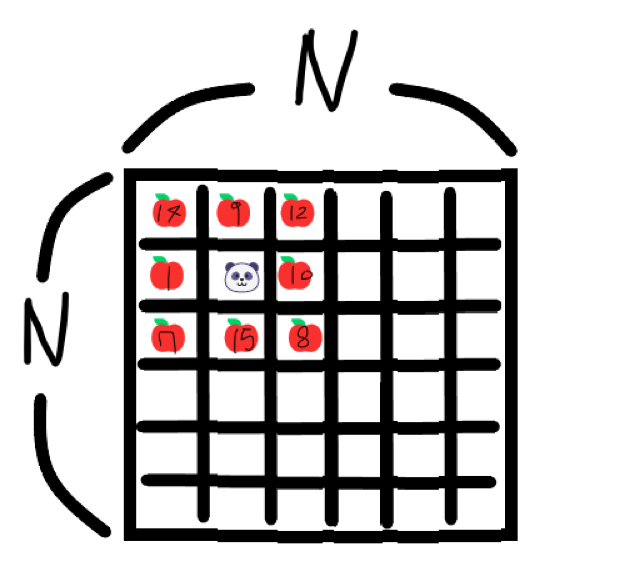
n x n의 크기의 대나무 숲이 존재합니다. (1 <= n <= 500)
-
욕심쟁이 판다는 어떤 지역에서 사과처럼 보이는 대나무를 먹기 시작 합니다.
-
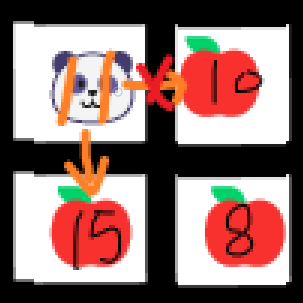
그 곳의 대나무를 모두 먹으면 상, 하, 좌, 우 중에 방금 대나무를 먹은 지역보다 대나무가 더 많은 지역으로만 이동합니다.
-
사진을 예로 들면 판다가 있는 곳의 대나무의 수가 11입니다. 주변을 둘러봤을 때 대나무의 수가 11보다 작은 10으로는 이동할 수 없고 15인 곳으로 이동이 가능합니다.
-
욕심쟁이 판다를 어떤 곳으로 옮겨야 최대한 많은 칸을 방문할 수 있을지 생각해보고 이동할 수 있는 칸의 수의 최댓값을 출력합니다.
🎯 문제 해결 방법
첫 번째 도전
문제를 보자마자 이 문제는 모든 칸을 시작점으로 확인했을 때 BFS 또는 DFS로 판다가 갈 수 있는 최대 이동 칸을 구하면 되겠구나! 생각을 하고 BFS로 코드를 작성하였습니다.
#define Y first #define X second전 pair를 사용할 때 first를 Y로 second를 X로 변환해서 사용합니다.
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define Y first
#define X second
using namespace std;
int n;
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int m[504][504];
int dist[504][504];
int main(void){
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
cin >> m[i][j];
}
}
int ret = 1;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
memset(dist, 0, sizeof(dist)); //시간 초과 발생
queue<pair<int,int>> q;
dist[i][j] = 1;
q.push({i,j});
while(!q.empty()){
auto cur = q.front(); q.pop();
for(int dir = 0; dir<4; dir++){
int nx = cur.X + dx[dir];
int ny = cur.Y + dy[dir];
if(nx < 0 || ny < 0 || nx >= n || ny >= n) continue;
if(dist[ny][nx] > 0) continue;
if(m[ny][nx] > m[cur.Y][cur.X]){
dist[ny][nx] = dist[cur.Y][cur.X] + 1;
q.push({ny,nx});
ret = max(ret, dist[ny][nx]);
}
}
}
}
}
cout << ret;
return 0;
}결론부터 말씀드리면 시간 초과가 발생하였습니다...

문제는 2중 for문에서 욕심쟁이 판다의 시작 점을 고를때마다 memset(dist, 0, sizeof(dist))을 통해 거리 배열을 0으로 초기화 해주면서 시간 초과가 발생했다고 판단했습니다.

두 번째 도전 들어갑니다!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
두 번째 도전
memset(dist, 0, sizeof(dist)) 지우고 다시 제출했습니다.
아까 보지 못했던 30%(채점 중)도 보이면서 "쉽다 쉬워 ㅋㅋ~" 하던 중


예?
메모리 초과요?
?????????????????????????????????????????????????????????????
설마하고 한번 더 제출해본거 맞습니다.
세 번째 도전
이 문제는 단순한 BFS/DFS 문제가 아니었습니다.
다른 분의 풀이를 확인해봤더니 DP + DFS의 방식으로 풀어야 시간 초과와 메모리 초과를 피할 수 있었던 문제였습니다.
DP는 탑-다운 형식인 메모이제이션(memoization)을 사용했습니다.
메모이제이션이란?
메모이제이션(memoization)은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다.
-위키백과-
dp[i][j] = k : (i, j)의 위치에서 시작한 욕심쟁이 판다가 이동할 수 있는 최대 칸 수
int func(int y, int x){
//메모이제이션의 핵심입니다. 갔던 곳은 추가로 확인하지 않습니다.
if(dp[y][x] != 0) return dp[y][x]; //값이 이미 있으면 바로 값을 반환합니다.
dp[y][x] = 1; //처음 가본 곳은 최소 1칸을 이동할 수 있다고 할 수 있기에 1로 초기화 해줍니다.
for(int dir=0; dir<4; dir++){ //현재 위치에서 상, 하, 좌, 우를 확인합니다.
int nx = x + dx[dir];
int ny = y + dy[dir];
if(nx < 0 || ny < 0 || nx >=n || ny >= n) continue;
if(m[ny][nx] > m[y][x]){ //대나무의 수가 더 많은 지역인지 확인합니다.
//현재 위치에서 갈 수 있는 최대 칸보다 ny, nx로 이동했을 때
//더 많은 칸을 이동할 수 있는지 비교해서 갱신합니다.
dp[y][x] = max(dp[y][x], func(ny,nx) + 1);
}
}
return dp[y][x];
}💻 정답 코드
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define Y first
#define X second
using namespace std;
int n;
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int m[504][504];
int dp[504][504];
int ret;
int func(int y, int x){
//메모이제이션의 핵심입니다. 갔던 곳은 추가로 확인하지 않습니다.
if(dp[y][x] != 0) return dp[y][x]; //값이 이미 있으면 바로 값을 반환합니다.
dp[y][x] = 1; //처음 가본 곳은 최소 1칸을 이동할 수 있다고 할 수 있기에 1로 초기화 해줍니다.
for(int dir=0; dir<4; dir++){ //현재 위치에서 상, 하, 좌, 우를 확인합니다.
int nx = x + dx[dir];
int ny = y + dy[dir];
if(nx < 0 || ny < 0 || nx >=n || ny >= n) continue;
if(m[ny][nx] > m[y][x]){ //대나무의 수가 더 많은 지역인지 확인합니다.
//현재 위치에서 갈 수 있는 최대 칸보다 ny, nx로 이동했을 때
//더 많은 칸을 이동할 수 있는지 비교해서 갱신합니다.
dp[y][x] = max(dp[y][x], func(ny,nx) + 1);
}
}
return dp[y][x];
}
int main(void){
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
cin >> m[i][j];
}
}
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
ret = max(ret, func(i,j));
}
}
cout << ret;
return 0;
}

