
이분 탐색이란❓
- 정렬되어 있는 배열에 특정 데이터가 있는지를 O(log n) 시간복잡도로 해결하는 알고리즘입니다.
- 어떠한 대상 데이터를 배열의 중간 데이터와 반복적으로 비교해서 원하는 데이터를 찾습니다.
- 또한, 이분 탐색(Binary Search)은 결정 문제(Decision Problem)의 답이 이분적일 때 사용할 수 있는 탐색 기법이라고도 합니다. 여기서 결정 문제란 답이 YES or NO 인 문제를 의미 합니다.
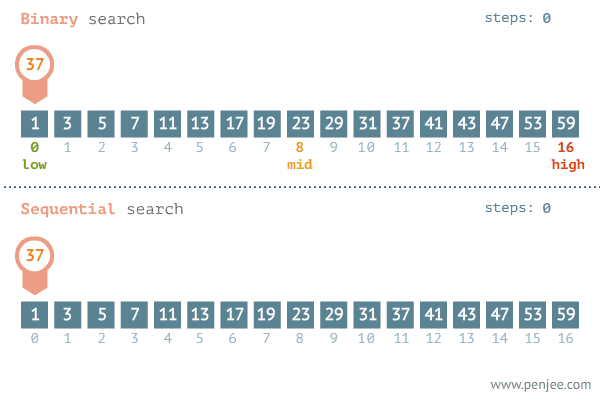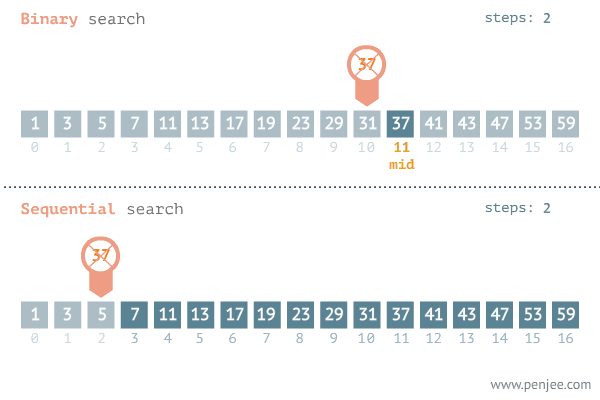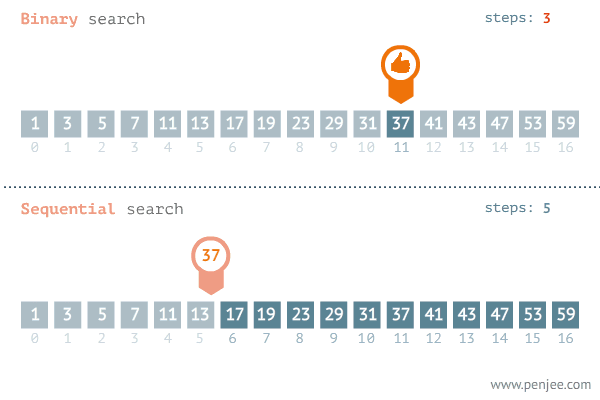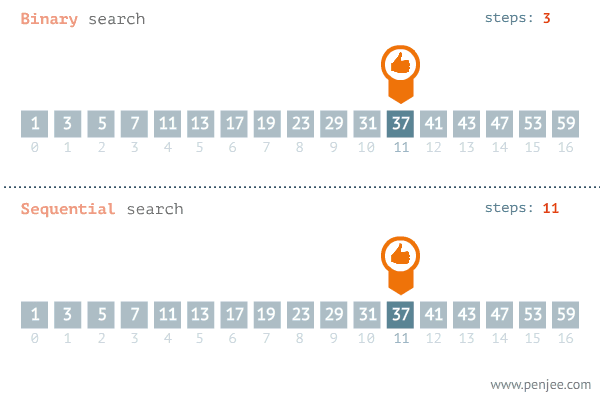
- 이 예시는 주어진 정렬된 배열에서 37의 숫자를 찾는 과정입니다.
- low, mid, high에 해당하는 세 개의 변수를 보통 사용하고 low를 배열의 시작, high을 배열의 끝, mid를 (low + high) / 2 를 하여서 중간을 가리키게 합니다.
- 위에서 결정 문제라는 용어는 mid 때문에 나온 것입니다. "지금 mid가 가리키는 값이 내가 찾는게 맞아? 아니야?"

- 37과 처음 비교하는 mid는 (0 + 16)/2 = 8 위치에 있는 23입니다.
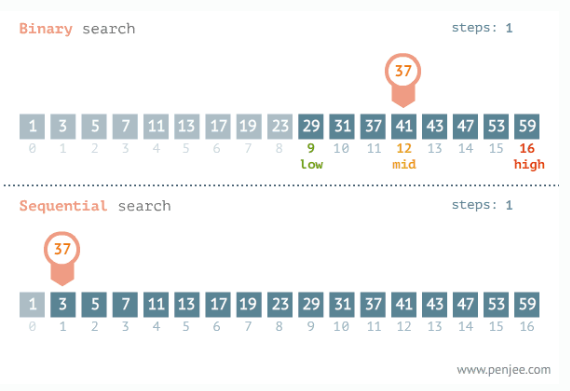
-
37은 23보다 크므로 low가 mid + 1 한 위치 29를 가리키게 합니다.
-
다음 mid는 (9 + 16) / 2 = 12.5 이므로 12 위치에 있는 41입니다.
-
high은 그대로입니다.
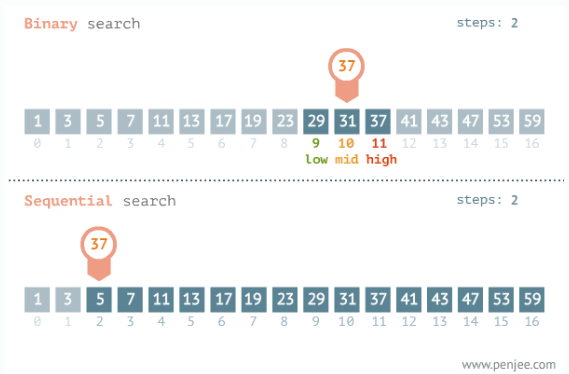
-
37은 41보다 작으므로 high가 mid - 1 한 위치 37를 가리키게 합니다.
-
거의 다 왔습니다. 다음 mid는 (9 + 11) / 2 = 10 위치에 있는 31을 가리킵니다.

- 37은 31보다 크므로 low의 값을 mid + 1 한 위치 37을 가리킵니다. 이러한 비교 과정을 통해 37을 찾게 됩니다.
💻 이분 탐색 구현 코드

문제 : 백준 14627 파닭파닥
- 파닭파닭 문제 정답 코드 중 일부를 가져왔습니다.
- 문제 설명이 아닌 이분 탐색 구현하는 코드만 설명하겠습니다.
- while 문이 핵심입니다.
int st = 1, en = 1e9;
int mid;
...
while(st <= en){
mid = (st + en) / 2;
if(chk(mid)){
ret = mid;
st = mid + 1;
}else{
en = mid - 1;
}
}
...bool chk(int mid){
int cnt = 0;
for(int i=0; i<s; i++){
cnt += d[i] / mid;
}
return cnt >= c;
}
- 시작 부분: st, 끝 부분 en,
en은 엄청 큰 수 또는 주어진 입력에서 제일 큰 값을 가리키게 하면 됩니다.
mid 의 값을 (st + en) / 2 로 정한 뒤 chk 함수를 통해서 이 mid 값이 정답이 되는게 맞아? 아니야? 결정문제로 만들어서 정답이 되는 mid 값이면 ret 변수에 담아줍니다.
🛠️ 이분 탐색 활용
1) lower_bound
- 찾으려는 key 값보다 같거나 큰 숫자가 배열 몇 번째에서 처음 등장하는지를 찾습니다.
2) upper_bound
- 찾으려는 key 값을 초과하는 숫자가 배열 몇 번째에서 처음 등장하는지를 찾습니다.
lower_bound와 upper_bound는 최대 증가 부분 수열 LIS(Longest Increase Sequence) 알고리즘에 사용되는 개념이므로 알아두면 좋을 것 같아 추가해보았습니다.
#include<iostream>
#include<algorithm> //lower_bound, upper_bound 사용하기 위해 선언해야함
using namespace std;
int main(void){
int a[6] = {1, 3, 5, 12, 12, 13};
int lower = *lower_bound(a, a+6, 12); //값
int lower_pos = lower_bound(a, a+6, 12) - a; //위치
int upper = *upper_bound(a, a+6, 12); //값
int upper_pos = upper_bound(a, a+6, 12) - a; //위치
cout << "lower : " << lower << " ,lower_pos : " << lower_pos << '\n';
cout << "upper : " << upper << " ,upper_pos : " << upper_pos << '\n';
return 0;
}위 코드 결과를 예상해봅시다
lower : ? , lower_pos : ?
upper : ? , upper_pos : ?'?' 에 각각 어떤 값이 들어갈까요 ??

답 생각해보셨나요?!

생각해보셨죠?!!?????????????!!!!!!
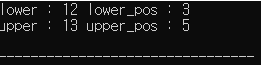
답은 이와 같습니다 :)
중요!!!!!!
이분 탐색을 활용하기 때문에 마찬가지로 lower_bound와 upper_bound는 꼭 정렬된 배열에서 사용해야합니다.
LIS 문제 추천
주어지는 입력 값이 너무 크면 DP보다는 이분 탐색으로 풀이해야합니다.
(DP로 풀어도 풀리는 문제)
가장 긴 증가하는 부분 수열
가장 긴 증가하는 부분 수열 4
(DP로 풀면 시간 초과, 이분 탐색으로 풀어야하는 문제)
가장 긴 증가하는 부분 수열 5
Python은 ?
파이썬 라이브러리 bisect 사용
JAVA는 ?
java.util.Arrays binarySearch 함수 사용
