
최단 경로 문제란?
그래프 이론에서 최단 경로 문제란 가장 짧은 경로에서 두 꼭짓점을 찾는 문제로서, 가중 그래프에서 구성하는 변들의 가중치 합이 최소가 되도록 하는 경로를 찾는 문제입니다.
1. 최단 경로 문제의 종류
-
단일-출발 최단 경로
- 어떤 하나의 정점에서 출발하여 나머지 모든 정점 까지의 최단 경로를 찾는 문제입니다.
-
단일-도착 최단 경로
- 모든 정점에서 출발하여 어떤 하나의 정점까지의 최단 경로를 찾는 문제로 그래프 내의 간선들을 뒤집으면 단일 출발 최단거리 문제로 바뀔 수 있습니다.
-
전체-쌍 최단 경로
- 그래프 내의 모든 꼭짓점 쌍들 사이의 최단 경로를 찾는 문제입니다.
2. 문제를 해결하기 위한 알고리즘 종류
1) 다익스트라 알고리즘
음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘
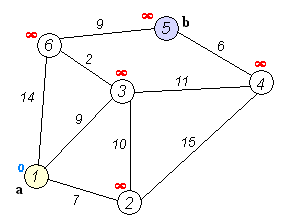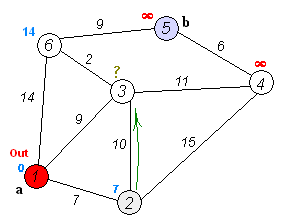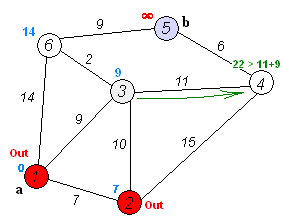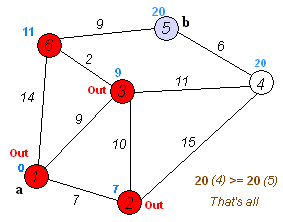
다익스트라 알고리즘은 다음과 같이 동작합니다.
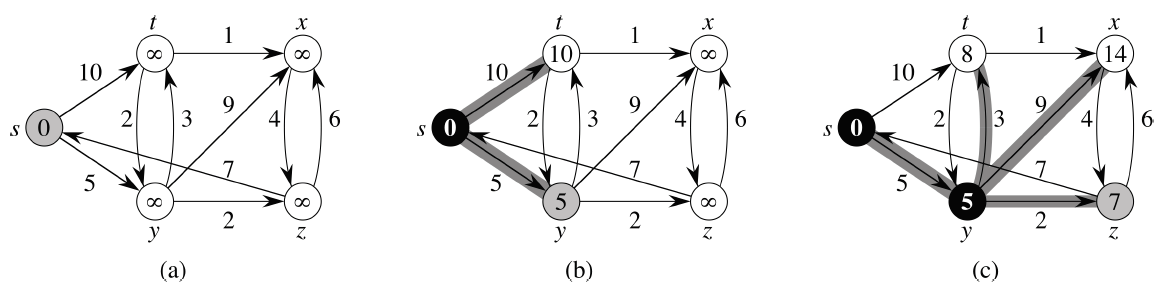
(a) 를 보면 시작 노드 s를 제외하고 모든 노드들의 거리 정보를 무한대로 설정합니다.
다익스트라는 기본적으로 BFS를 활용합니다. (b)를 보면 s를 기준으로 BFS를 적용시키면 s에 이웃한 t와 y의 거리 정보를 업데이트합니다. 방문을 마친 s는 검은색으로 칠해준 뒤 다음으로 방문하는 곳은 이웃한 노드들 중에서 거리가 가장 최소인 노드를 골라 방문합니다. 현재 탐색하고 있다는 뜻으로 회색을 칠해줍니다.
(c) 도 (b)와 마찬가지로 현재 방문중인 y에서 BFS를 적용시켜서 y에 이웃한 t, x, z 의 거리 정보를 업데이트 한 뒤 거리가 가장 최소인 노드를 골라 방문하는 과정을 반복합니다.
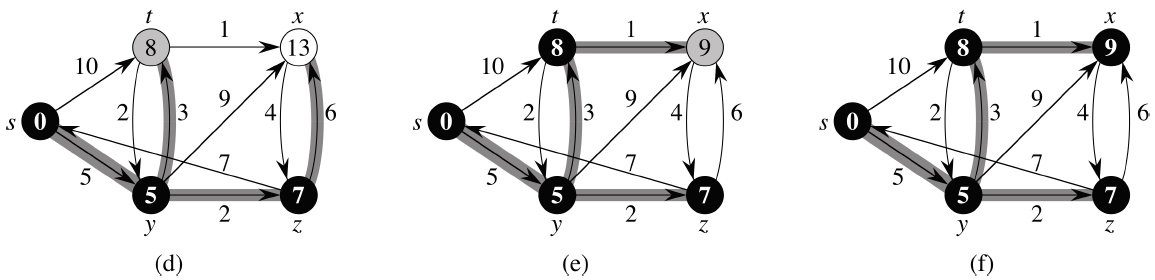
나머지 노드들도 모두 확인하면 s에서 다른 노드들로 갈 때 최단 거리를 구할 수 있게 됩니다.
2) 벨만-포드 알고리즘
- 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘
- 간선의 가중치가 음수일 때도 최단 거리를 구할 수 있습니다.
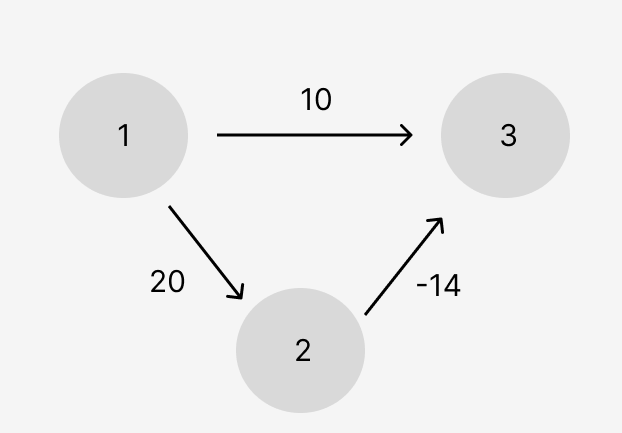
위에서 알아본 다익스트라 알고리즘과 벨만-포드 알고리즘은 무엇이 다를까요?
그림으로 살펴보겠습니다.
1번 노드에서 3번 노드로 가는 최단 거리를 구하고자 할 때 두 가지 경로가 있습니다.
- (1) -> (3) : 10
- (1) -> (2) -> (3) : 20 - 14 = 6
이 그림에서는 최단 거리는 6으로 구할 수 있어야합니다.
다익스트라 알고리즘을 사용하면 1번 노드에서 다음 노드를 구할 때 가중치가 10인 3번 노드를 고르는 첫 번째 경로를 선택하게 됩니다.
반면에 벨만-포드 알고리즘을 사용하면 항상 모든 간선을 확인하므로 두 번째 경로를 선택하면서 최단 거리 6을 구할 수 있습니다.
즉, 다익스트라 알고리즘은 경로에 음수의 가중치가 존재하면 최단 거리를 구할 수 없지만 모든 간선을 확인하는 벨만-포드 알고리즘은 음수의 가중치가 존재하더라도 최단 거리를 구할 수 있습니다.
3) A* 탐색 알고리즘
A* 알고리즘은 그래프의 최단 경로 문제를 푸는 알고리즘으로 다익스트라 알고리즘을 발전시킨 알고리즘입니다. 다익스트라 알고리즘은 시작 지점에 가까운 지점부터 순서대로 결정하기 때문에 종점에서 멀어지는 방향의 정점의 최단 경로도 결정해나가지만, 이것들은 결국 쓰이지 않기 때문에 불필요합니다.
A* 알고리즘은 미리 추정 비용을 힌트로 설정해서 그 정보를 이용하는 것으로 불필요한 탐색을 줄이도록 발전시킨 알고리즘입니다.

주로 게임에서 플레이어를 목표 지점으로 이동시킬 때 사용하는 알고리즘입니다.
f(n) = g(n) + h(n)
g(n) : 시작 노드부터 현재 노드까지의 비용
h(n) : 현재 노드에서 목표 노드까지의 예상 비용
이 두 값을 더한 f(n)이 가장 최소가 되는 노드를 다음 탐색 노드로 선정합니다. 다익스트라와 마찬가지로 이 알고리즘도 대체로 우선순위 큐를 사용합니다.
현재 노드에서 목표 노드까지의 예상 비용을 구하는 함수 h(n)을 휴리스틱 함수라고 합니다.
휴리스틱 함수로는 맨해튼 거리 함수와 유클리디안 거리 함수가 있습니다.
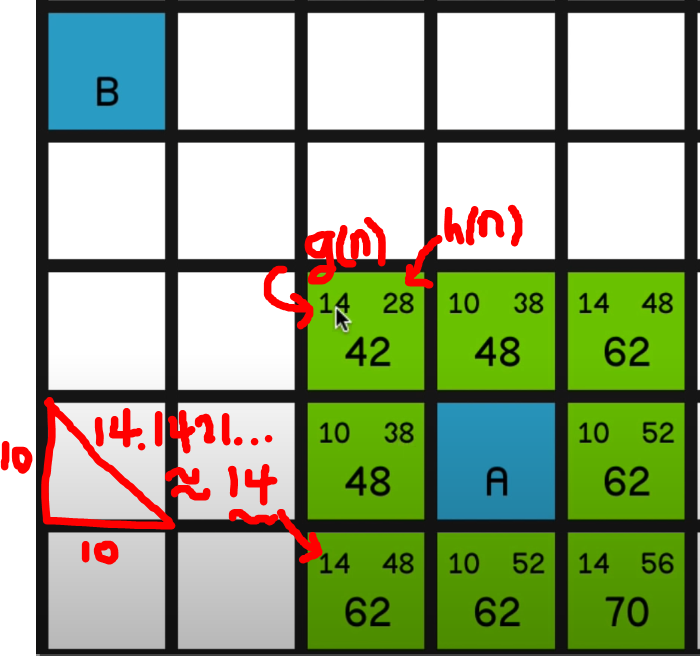
시작 노드(A)와 목표 노드(B)가 있을 때 A 주변 노드의 f(n)을 구하면 위 그림과 같습니다.
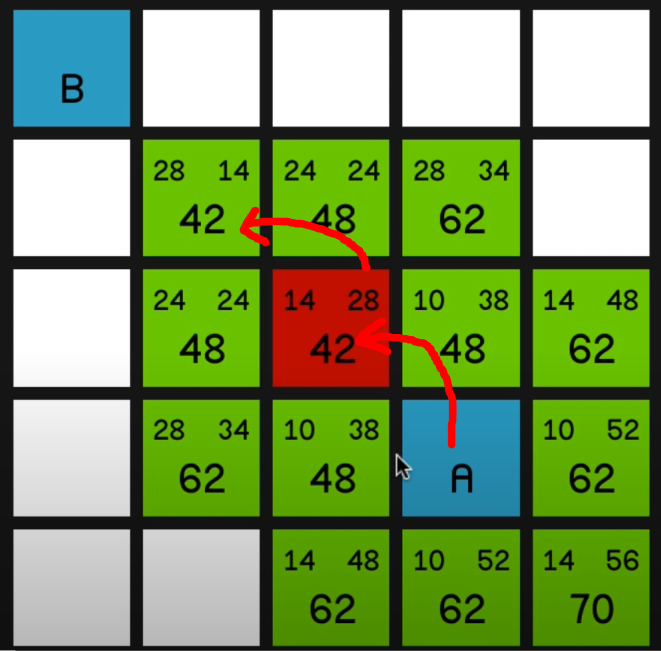
가장 작은 f(n)을 가진 노드를 찾아가는 과정을 반복해서 목표 노드 B에 도착합니다.
4) 플로이드-워셜 알고리즘
그래프에서 가능한 모든 노드 쌍에 대해 최단 거리를 구하는 알고리즘이다.
모든 노드간의 최단거리를 구해야 하는 플로이드-워셜은 2차원 인접 행렬을 사용합니다.
라운드마다 각 경로에서 새로운 중간 노드로 사용할 수 있는 노드를 선택하고, 더 짧은 길이를 선택하여 줄이는 과정을 반복합니다.
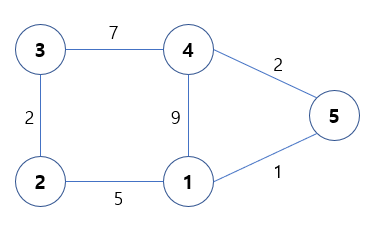
위 그림을 인접 행렬로 표현하면 아래와 같습니다. 이 예시에서는 1~5번 노드까지 존재하므로 다섯 번의 라운드가 존재합니다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0 | 5 | INF | 9 | 1 |
| 2 | 5 | 0 | 2 | INF | INF |
| 3 | INF | 2 | 0 | 7 | INF |
| 4 | 9 | INF | 7 | 0 | 2 |
| 5 | 1 | INF | INF | 2 | 0 |
첫 번째 라운드에서 1번 노드를 새로운 중간 노드로 설정하게 되면
| 노드 번호 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0 | 5 | INF | 9 | 1 |
| 2 | 5 | 0 | 2 | 14 | 6 |
| 3 | INF | 2 | 0 | 7 | INF |
| 4 | 9 | 14 | 7 | 0 | 2 |
| 5 | 1 | 6 | INF | 2 | 0 |
2번에서 4번으로 가는 길은 원래는 INF 로 길이 없음을 나타냅니다. 하지만 1번 노드를 중간 노드로 선정하게 되면 2 -> 1 -> 4 로 가는 길이 생기고 5 + 9 = 14 로 업데이트 해줍니다.
중간 노드를 1~5번으로 설정하면서 계속 반복하다 보면 모든 노드 간 최단 거리를 구할 수 있게 됩니다.
[Reference]
- https://ratsgo.github.io/data%20structure&algorithm/2017/11/26/dijkstra/
- https://velog.io/@kimdukbae/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%B2%A8%EB%A7%8C-%ED%8F%AC%EB%93%9C-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Bellman-Ford-Algorithm
- https://ko.wikipedia.org/wiki/%EC%B5%9C%EB%8B%A8_%EA%B2%BD%EB%A1%9C_%EB%AC%B8%EC%A0%9C
- https://kangworld.tistory.com/61
- https://chanhuiseok.github.io/posts/algo-50/
