graph & tree (1)

i do as i say·2020년 5월 7일

안녕하세요? 디카페인으로 활기를 충전하는 아침입니다. 옛날엔 이걸 무슨 맛으로 먹냐며... 차대를 했는데요... 나이가 점점 드니(?) 지금은 그냥 카페 들어가면 디카페인 아메리카노만 시키고 있습니다. ㅋㅋ 생존 본능이 아메리카노를 찾네요. 대한민국 열공러들 파이팅입니다.

Graph와 Tree에 대해서 정리해 봅니다. Graph, tree, Binary search tree 이렇게 3탄으로 구성되어 있어요. 그런데 사실 이 세 개 전부 graph라는 큰 뿌리에서 나온 갈래들일 뿐입니다.

graph 자료 구조?

이때까지 제가 배운 자료 구조는 일자로 된 자료 구조였는데요. (linked-list Stack, Queue 등) 이번엔 그물처럼 엉켜 버린(?) 모양새를 띄고 있습니다. 그래서 그래프 자료 구조는 일직선이 아니다 하여 non-linear data structure라고 말합니다.

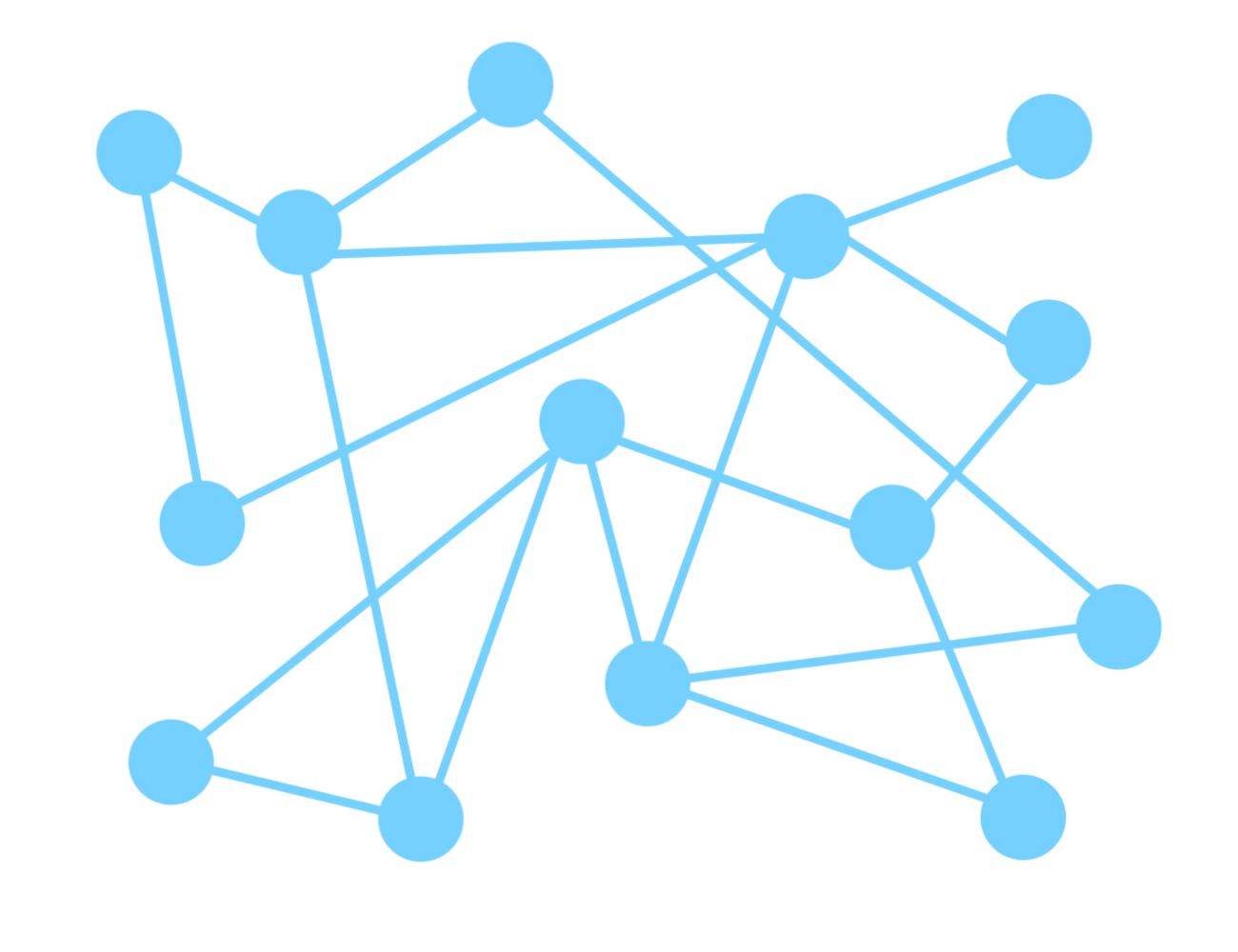
이런 모양인데요. 처음 본 제 느낌은... " 이게 뭐야? 이걸 어떻게 공부해? 이렇게 해서 되는 게 있어? 어떻게 찾아? 어떻게 넣어? 왜 이렇게 복잡하고 정리가 안 된 느낌이야? " 였습니다. 하하. 그런데 다 방법이 있더라구요. 약간 약 파는 사람처럼 말하고 있네요.

그래프는 정말 저게 다예요. 연결되어 있는 점(..)들의 관계를 나타내고, 표현이 가능한 자료 구조인데요, 보시면 이리저리 엉켜 있죠? 그만큼 자유롭습니다. 내비게이션이나 지하철 경로 등, 최단 / 최소 비용 찾기에 굉장히 효과적인 자료 구조입니다.

graph의 특징은 뭐예요..?

한 버텍스에서 2개 이상의 경로가 가능합니다.
노드들 사이에 무뱡향 / 방향에서 양뱡향 경로를 가질 수 있습니다.
selp loop뿐만 아니라 loop circult도 완죤 가능합니다.
루트와 노드의 개념이 아니고, 부모와 자식 관계도 아니구요.
그래프는 순환과 비순환으로 나뉩니다.

그림으로 보면 훨씬 이해가 쉽습니다. 용어 설명과 함께 바로 그림으로 보시죠!

graph에서 쓰이는 용어들이 있나요?

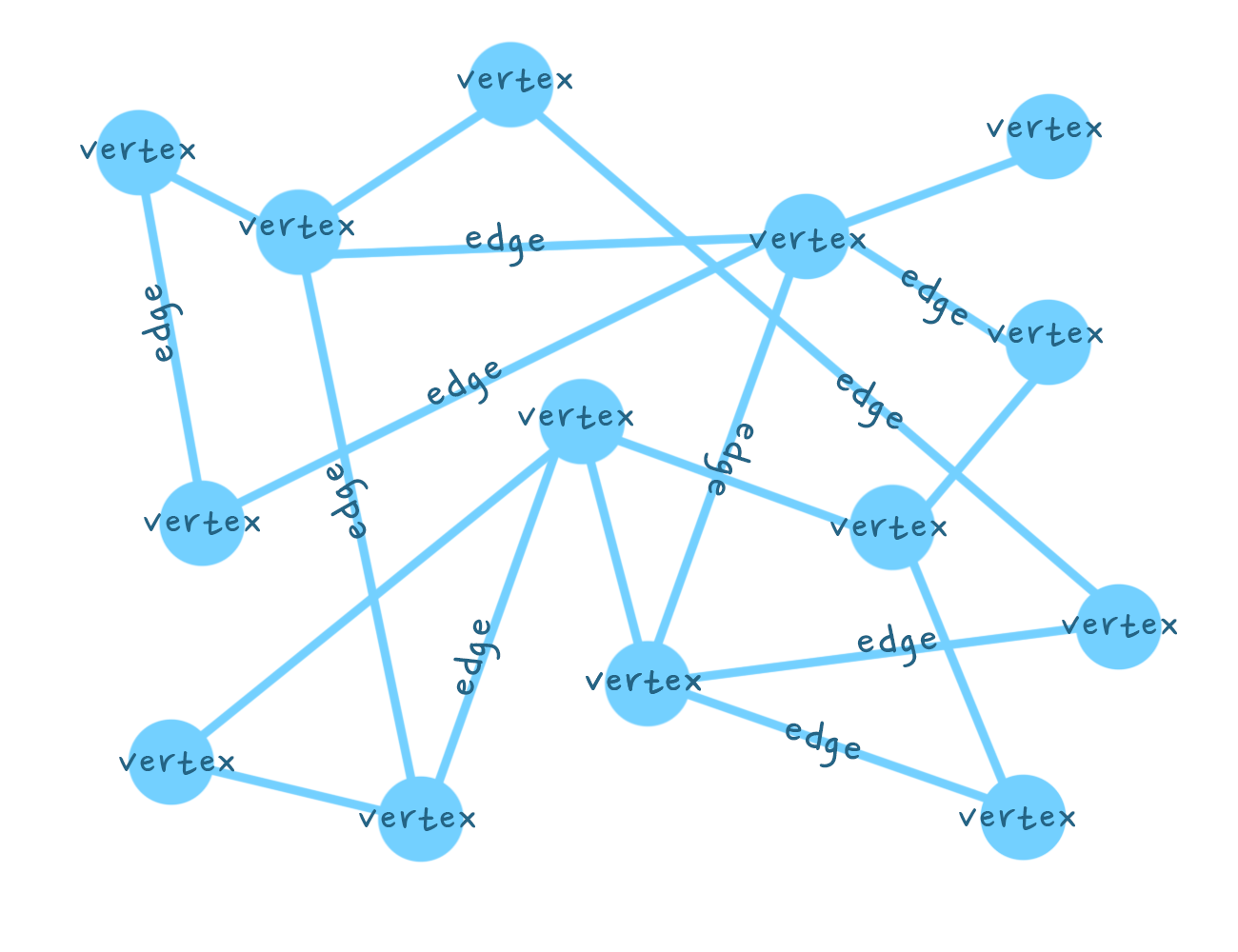
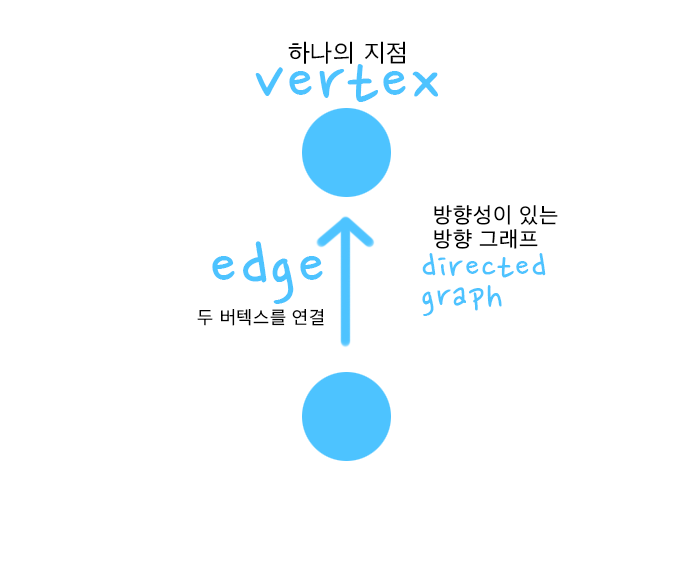
점이라고 말했던 것은 데이터입니다. 데이터를 정점, 즉, vertex라고 부릅니다.
그리고 점과 점을 이어 주는 간선은 edge라고 부릅니다.

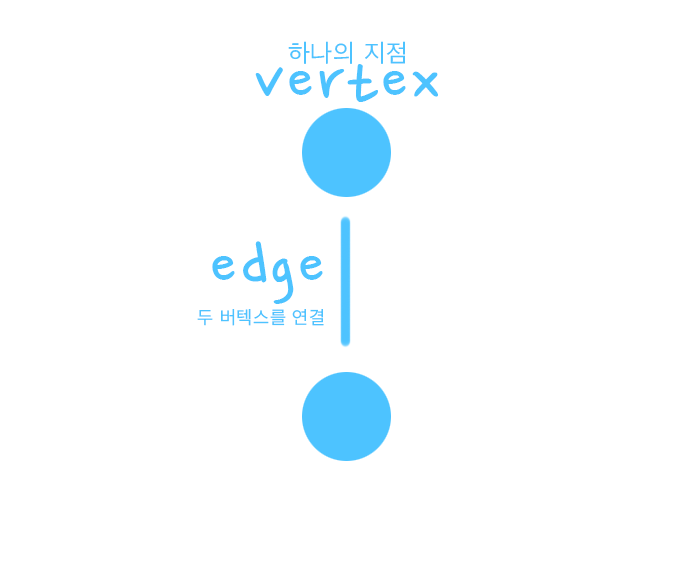
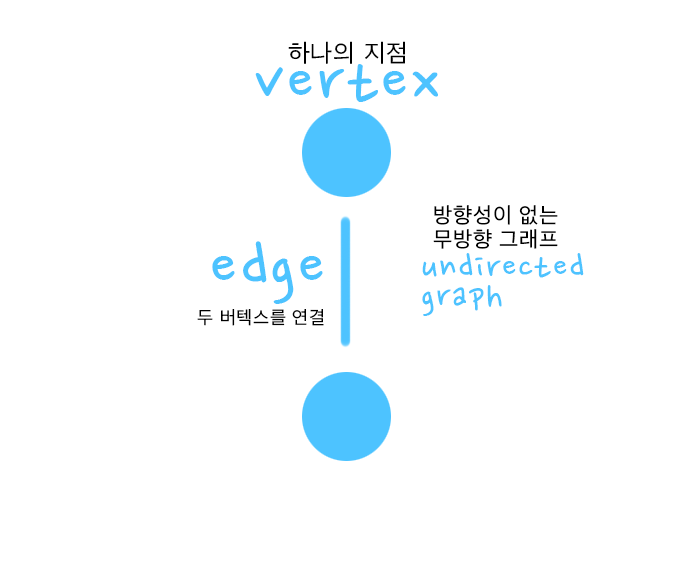
두 버텍스 간의 연결에 방향성이 없는 무방향 그래프, 언다이렉트 그래프

요 무방향 그래프는 간선을 통해 양방향이 가능합니다. 그래서 구현을 할 때, A와 B 모두에게 연결을 해 줘야 되고, A만 연결하게 되면 방향 그래프로 변질이 될 수 있습니다.

두 버텍스 간의 연결에 방향성이 있는 방향 그래프, 다이렉트 그래프
간선에 방향성이 있는 그래프로, 일방 통행입니다. A -> B를 연결했을 때, 무방향이라면 B -> A도 가능하겠지만 방향 그래프는 일방 통행이기 때문에 A -> B밖에 갈 수 없습니다.

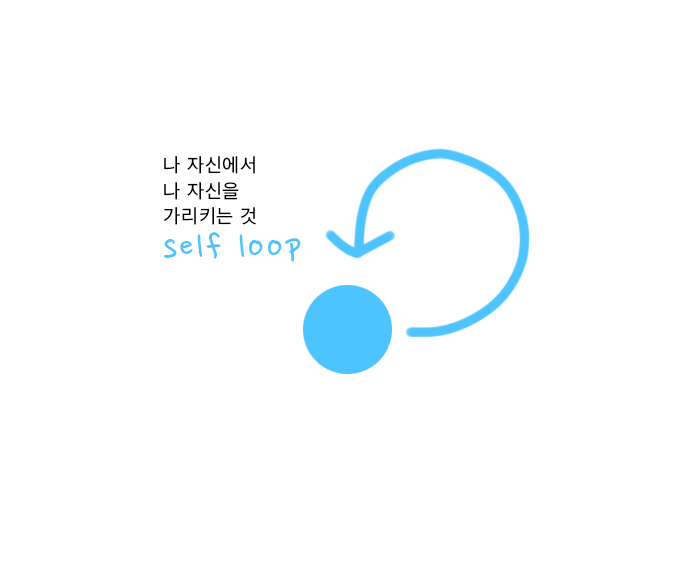
나 자신에서 나를 가리키는 self loop

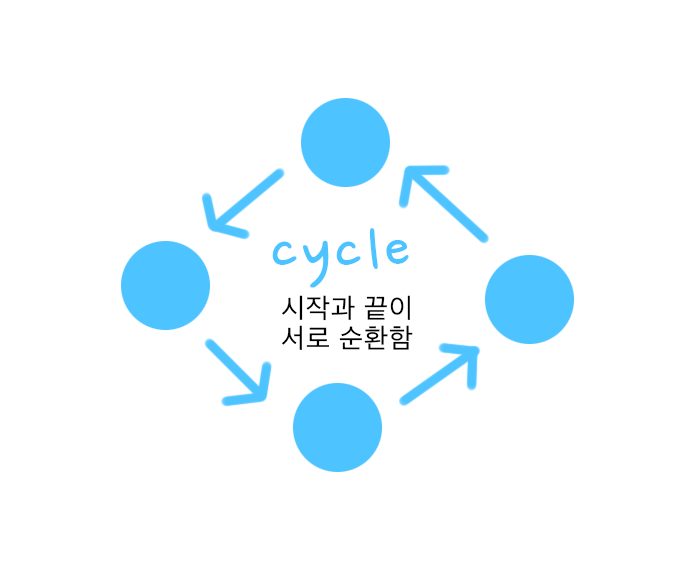
시작과 끝이 같은 cycle

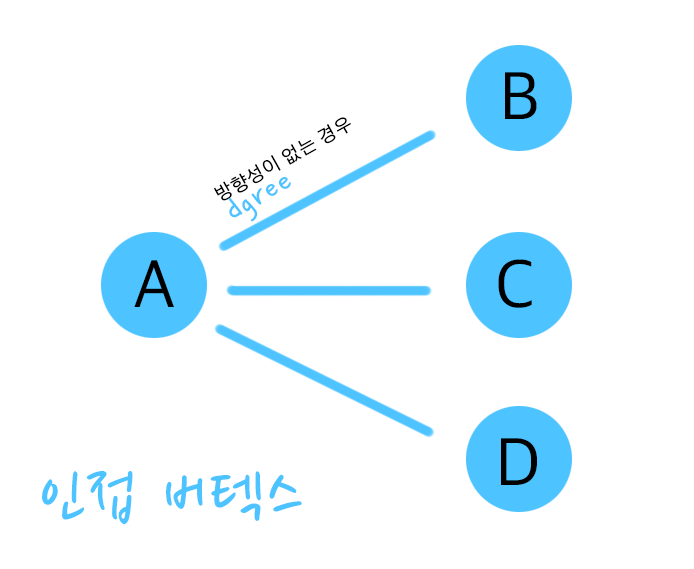
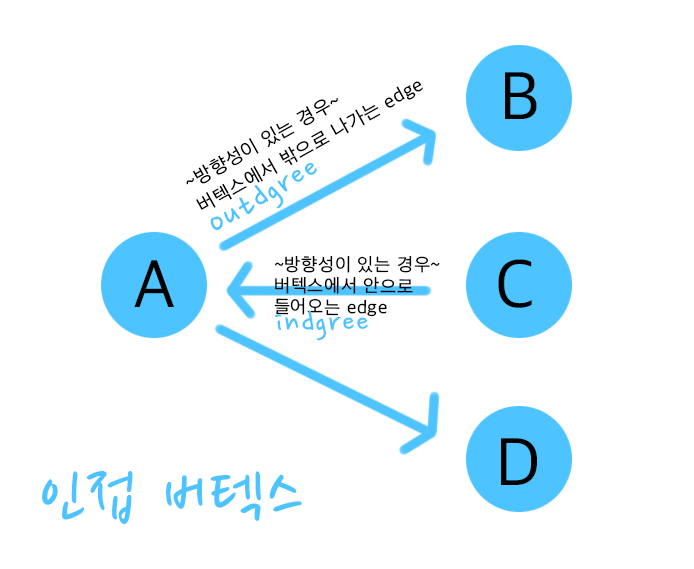
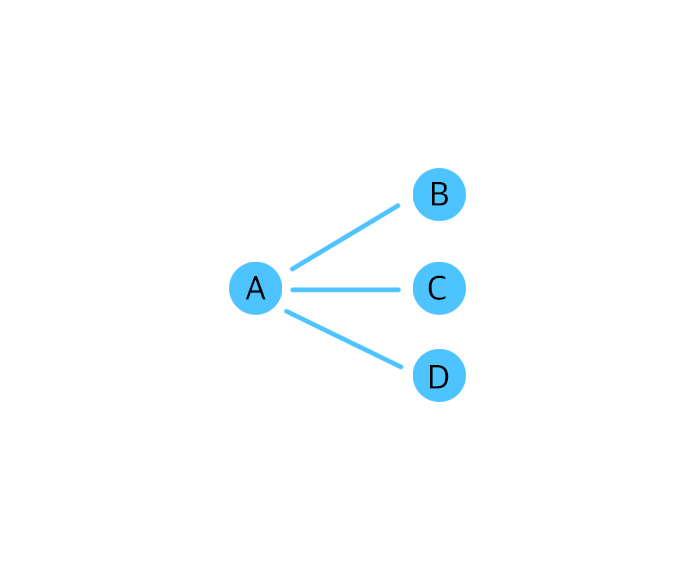
버텍스에서 직접적으로 이어져 있는 버텍스들을 인접 버텍스라고 하고, 또 그 선들을 디그리(degree)라고 하는데요, 하단에 있는 그림일 경우, A의 인접 버텍스는 3 개가 되고, B, C, D는 1 개가 되겠죠?

방향성이 있을 땐 그 방향에 따라 이름이 나뉘는데요, 버텍스에서 바깥으로 나가는 엣지를 outdegree, 버텍스에서 안으로 들어오는 경우를 indegree라고 합니다.

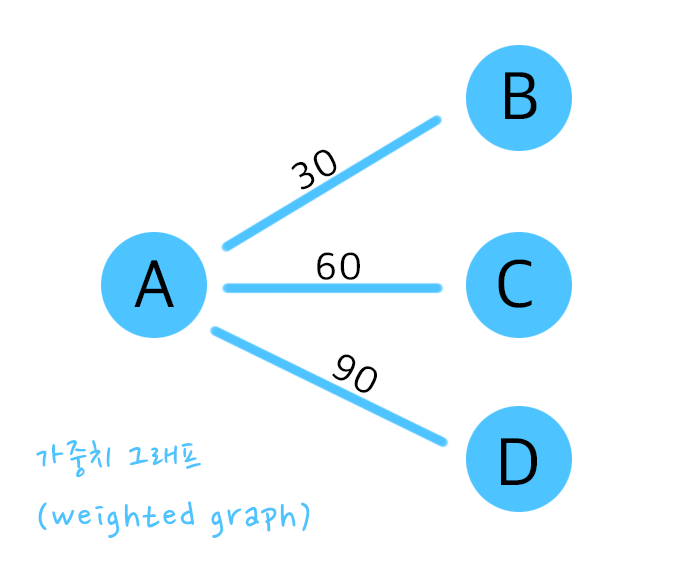
엣지에 비용이나 가중치가 할당이 된 그래프도 있는데요, 이는 도시와 도시를 연결하거나 도로, 길, 통신망 사용료 같은 어떠한 경로를 탐색할 때 들여지는 시간이나 비용 등을 나타낼 수 있습니다.

그래프에 속해 있는 모든 버텍스가 서로 연결이 되어 있는 그래프인 완전 그래프가 있는데요, 이것은 "한 붓 그리기"로 유명한데요,

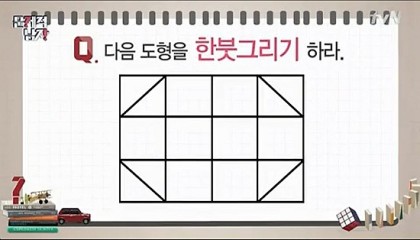
오일러 경로라고도 부릅니다. 그래프에 존재하는 모든 엣지를 한 번만 통과하게 되면 처음 정점으로 돌아오는 경로를 일컫습니다. 그래프의 모든 정점에 연결된 간선의 개수가 짝수일 때 가능합니다.

graph 구현하는 방법

(무려) 두 가지 방법이 있습니다.

인접 리스트(Adjacency list)와 인접 행렬(Adjacency Matrix)입니다.

인접 행렬

	A	B	C	D
A	X	O	O	O
B	O	X	X	X
C	O	X	X	X
D	O	X	X	X

2차원 배열에 모든 버텍스의 연결 관계를 담는 방식입니다.
0과 1을 이용한 정수 행렬로 표현할 수 있습니다.

if(간선[a][b] === 1) // 연견되어 있음
if(간선[a][b] !== 1) // 연결되어 있지 않음

NxN으로 만들어지기 때문에, 간선의 수와 무관하게 n^2의 메모리 공간이 필요합니다. 그래서 버텍스를 잇는 엣지의 여부를 O(1)안에 찾을 수 있는 장점이 있지만, 순회를 해야 될 때는 전부 다 돌아야 되기 때문에 그래프에 간선이 많은 밀집 그래프일 때 좋습니다.

인접 리스트

일반적인 방법입니다. 버택스 객체 안에 입접 버택스 리스트를 저장하는 건데요, 이름이 '리스트'가 들어가니, 감이 오시죠? 연결 리스트나 배열 등, link와 비슷한 구조로 들어가게 됩니다.

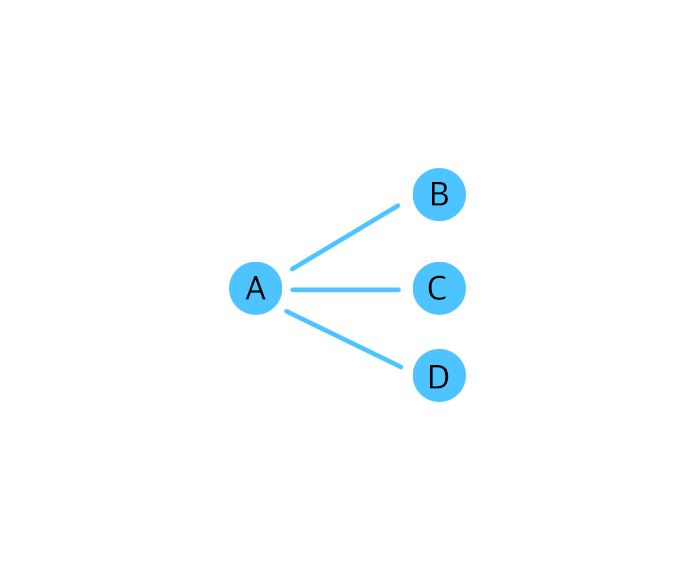
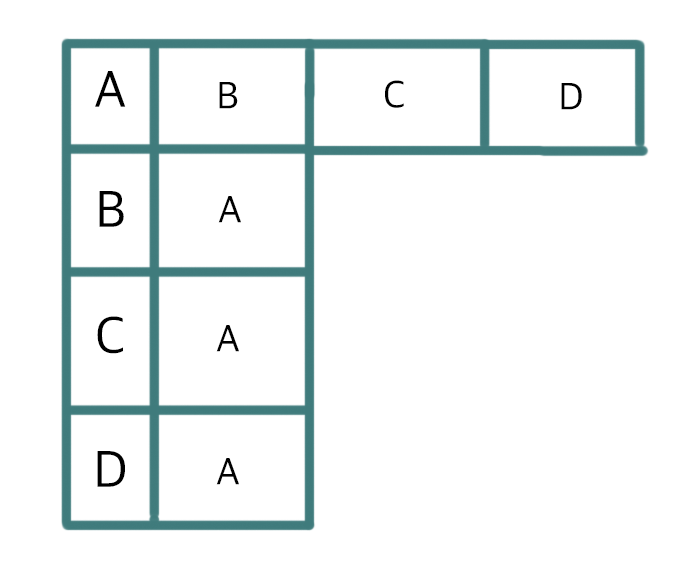
버텍스의 번호만 알게 된다면 이 번호를 배열의 인덱스로 해서, 각 버텍스의 리스트에 쉽게 접근할 수 있습니다.

무방향에서는 두 번씩 저장해야 서로 이어질 수 있습니다.

인접 노드를 쉽게 찾을 수 있고, 그래프에 존재하는 모든 간선의 수를 O(n+e)안에 알 수 있습니다. 확실히 인접 행렬보다 메모리 차지 비중이 크기 때문에 그래프 내에 적은 숫자만을 가지는 그래프에 용이하구요.

인접 리스트와 인접 행렬은 어떨 때 쓰나요?

인접 리스트: 하나의 버텍스를 기준으로, 탐색을 자주할 때.
인접 행렬: 버텍스와 버텍스간의 엣지를 자주 탐색할 때.

JS로 무방향 graph 구현하기

(객체로도 구현하고 배열로도 구현했었는데 일단은 배열로만... 객체는 나중에, 여유로울 때 함 정리해 봅니다...)

addNode : 그래프에 노드 추가하기
contains: 그래프에 해당 노드가 있는지 확인
removeNode: 노드 삭제하기
hasEdge: 노드와 노드 사이에 엣지가 있는지 확인
addEdge: 노드와 노드 사이에 엣지 추가
removeEdge: 노드와 노드 사이의 엣지 삭제

수도코드

addNode(node)

constructor로 만든 node객체에 추가할 node를 키로 설정하고, 값도 똑같이 node객체에 추가할 node를 키로 설정과 함께 배열 만들기.

contains(node)

만약 this.node[node]가 존재한다면 true, 아니라면 false를 반환.

removeNode(node)

만약 지우려는 노드가 없다면 undefined를 리턴한다.
this.node[node]의 길이가 0이 아니라면? (엣지가 1개 이상이라면?)
2-1. removeEdge()를 사용해서 해당 노드와 해당 노드에 연결된 노드의 엣지까지 삭제해 줌.
노드 삭제
객체 반환

hasEdge(fromNode, toNode)

fromNode를 반복문으로 돌려서 해당 인덱스가 toNode를 가지고 있는지 확인
맞으면 트루, 아니면 폴스.

addEdge(fromNode, toNode)

push로 from과 to의 노드 전부에 각자 엣지를 연결해 줌.

removeEdge(fromNode, toNode)

pop으로 from과 to의 노드 전부에 각자 엣지를 삭제해 줌.

JS CODE

/* Undirected Graph */
class Graph {
  constructor() {
    this.nodes = {};
  }

  addNode(node) {
    this.nodes[node] = this.nodes[node] || []
  }

  contains(node) {
    if (this.nodes[node]) {
      return true;
    }

    return false;
  }

  removeNode(node) {
    if (!this.nodes[node]) {
      return undefined;
    }

    else {
      if (this.nodes[node].length !== 0) {
        for (let edge of this.nodes[node]) {
          this.removeEdge(node, edge);
        }
      }
      delete this.nodes[node];
      return this.nodes;
    }
  }

  hasEdge(fromNode, toNode) {
    for (let i of this.nodes[fromNode]) {
      if (i === toNode) {
        return true;
      }
    }

    return false;
  }

  addEdge(fromNode, toNode) {
    this.nodes[fromNode].push(toNode);
    this.nodes[toNode].push(fromNode);

  }

  removeEdge(fromNode, toNode) {
    this.nodes[fromNode].pop(toNode);
    this.nodes[toNode].pop(fromNode);

  }
}