그래프와 트리의 두 번째 시간입니다.

---

Tree 구조

언제나 항상 느끼지만 이름을 참 직관적으로 잘 짓는 것 같습니다. 이 트리 구조는 그래프의 여러 구조 중 일방향 그래프의 한 구조인데요, 나무와 닮아 있다고 해서 트리 구조라고 이름을 붙였습니다.

하나의 뿌리로부터 가지가 사방으로 뻗은 형태를 띄고 있기 때문인데요.

사진 참고: 위키

이렇게 하나의 루트에서부터 계속 뻗어 있습니다. 제일 상단에 있는 것을 root, 뿌리라고 하구요. 트리 구조를 거꾸로 보면 나무와 비슷하다는 것을 알 수 있습니다.

자, 그러면 tree 자료 구조에 대해서 알아봅시다!

tree 구조에 대해서

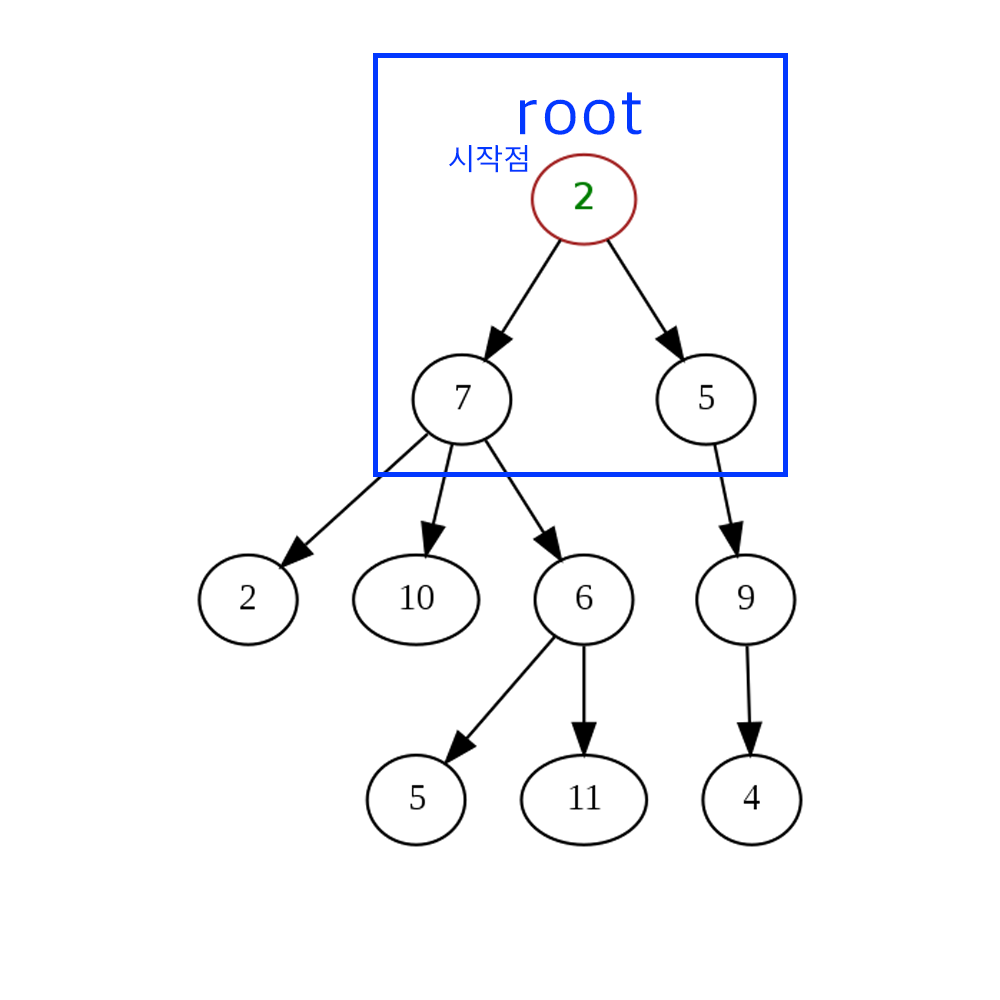
트리 구조의 기본입니다. 시작점을 root라고 합니다.

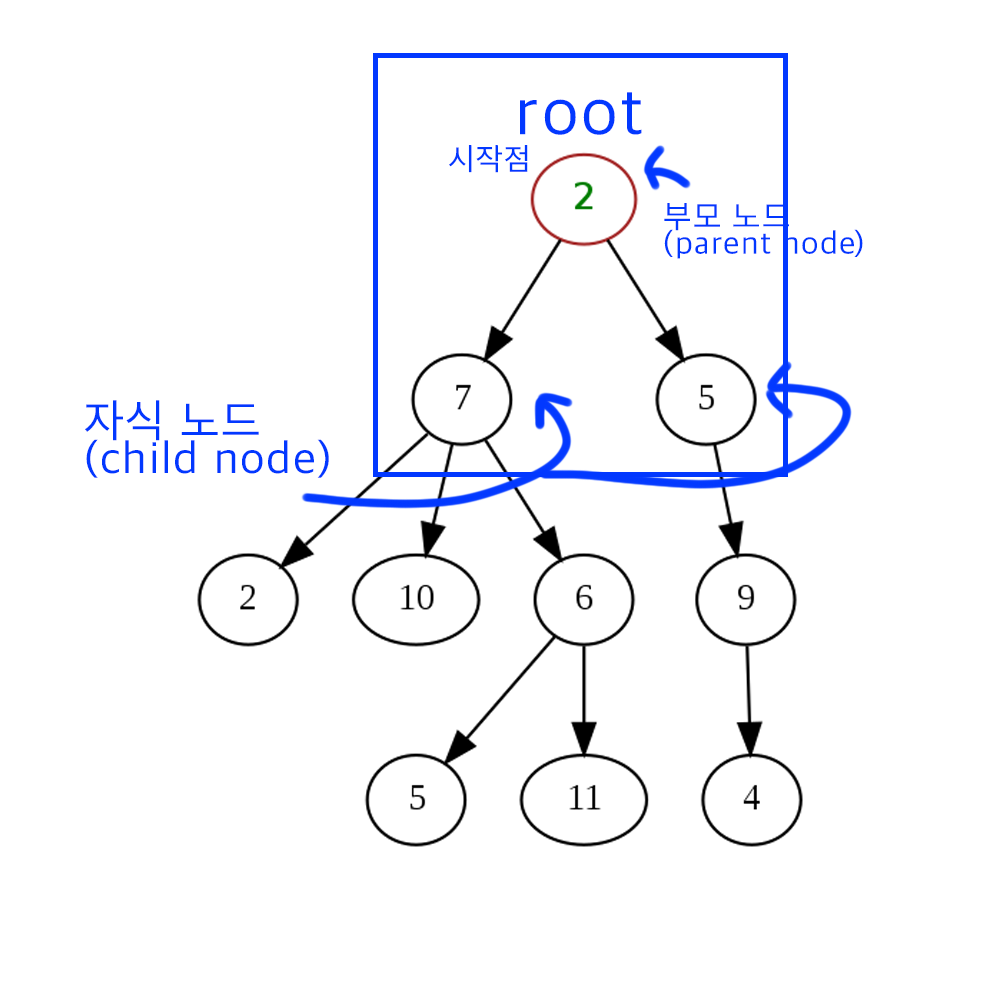
시작점만이 부모 노드는 아닙니다. 아래에 자식 노드를 두고 있으면 부모 노드로 인식을 합니다.

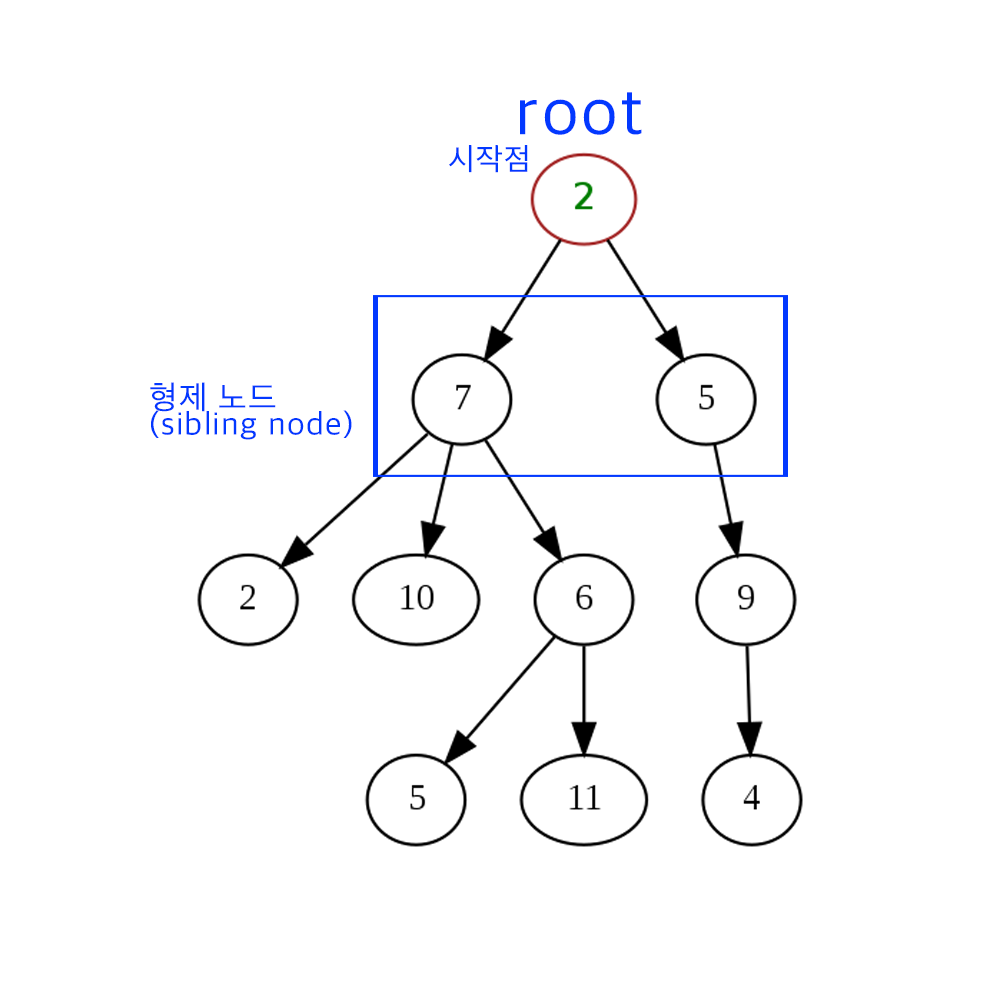
같은 부모 노드에 붙어 있는 child node들을 묶어서 부를 땐 형제 노드라고 부릅니다.

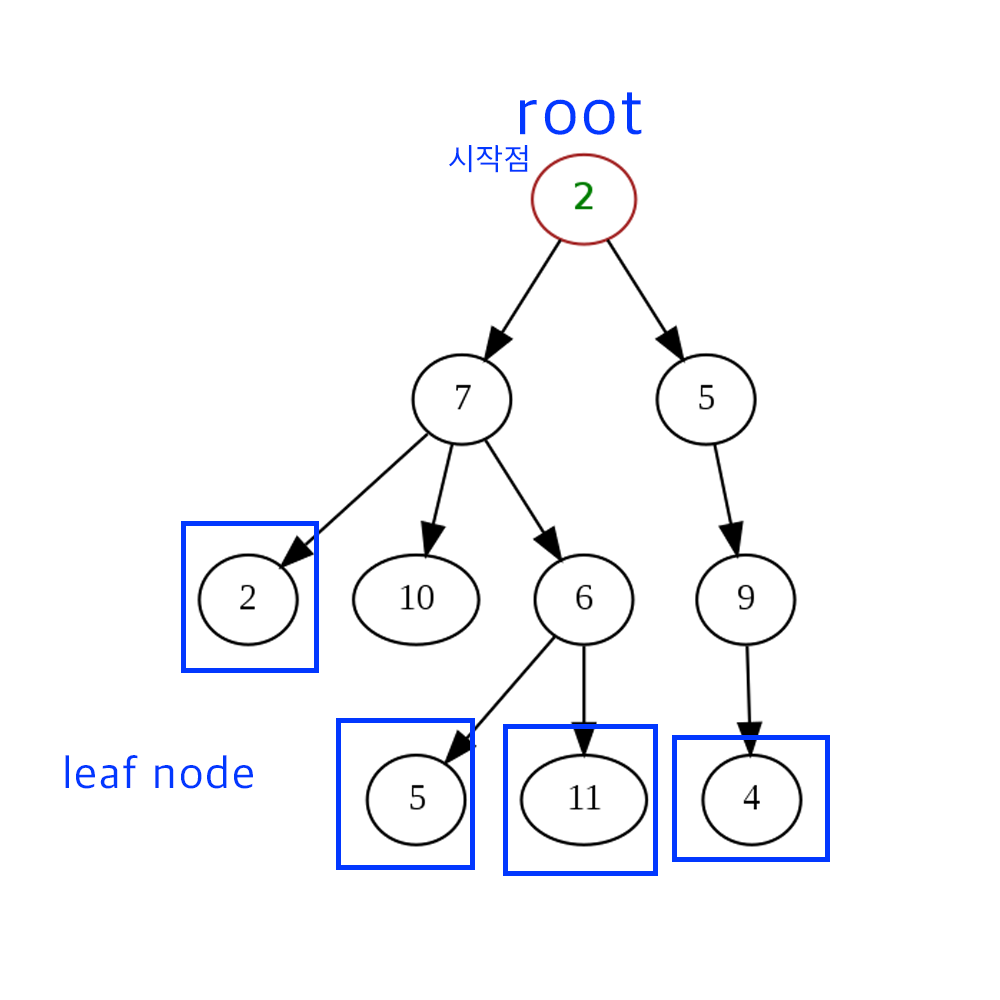
더 이상의 자식 노드가 없는 노드는 나뭇잎과 같다고 해서 leaf node라고 부릅니다.

노드가 N개인 트리는 항상 N-1개의 엣지를 가지게 되고, 트리 루트에서 뻗어져 나오기 때문에 루트에서 어떠한 경로로 가는 경로는 유일합니다.

tree와 graph의 차이?

graph: 2개 이상의 경로가 가능, 무방향에서 양방향으로도 가능.
자기 자신을 돌 수 있고, loop도 가능합니다.
루트 노드 개념이 없고, 부모-자식 개념도 없습니다.
그래프 순회는 DFS, BFS로 이루어져 있습니다.
그래프는 네트워크 모델입니다.

tree: 트리는 그래프의 특별한 케이스이며, "최소 연결 트리"라고도 불립니다.
루트 노드 개념이 있고, 부모-자식 개념도 있습니다.
자기 자신을 돌 수 없음은 물론이고 loop 순환도 불가합니다.
부모-자식 관계의 흐름은 상하입니다.
트리의 순회는 전위, 중위, 후위 순환으로 이어지고, 이것들은 모두 그래프의 DFS, BFS 안에 있습니다.
트리에는 종류가 많습니다. (이진트리, 이진탐색트리, AVL트리, 힙트리 등)
트리는 계층 모델입니다.

(https://sexycoder.tistory.com/79)

tree depth & height

트리에는 깊이와 높이의 개념도 존재합니다.

트리의 높이는 root로부터 얼마큼 내려와 있는지를 확인합니다.

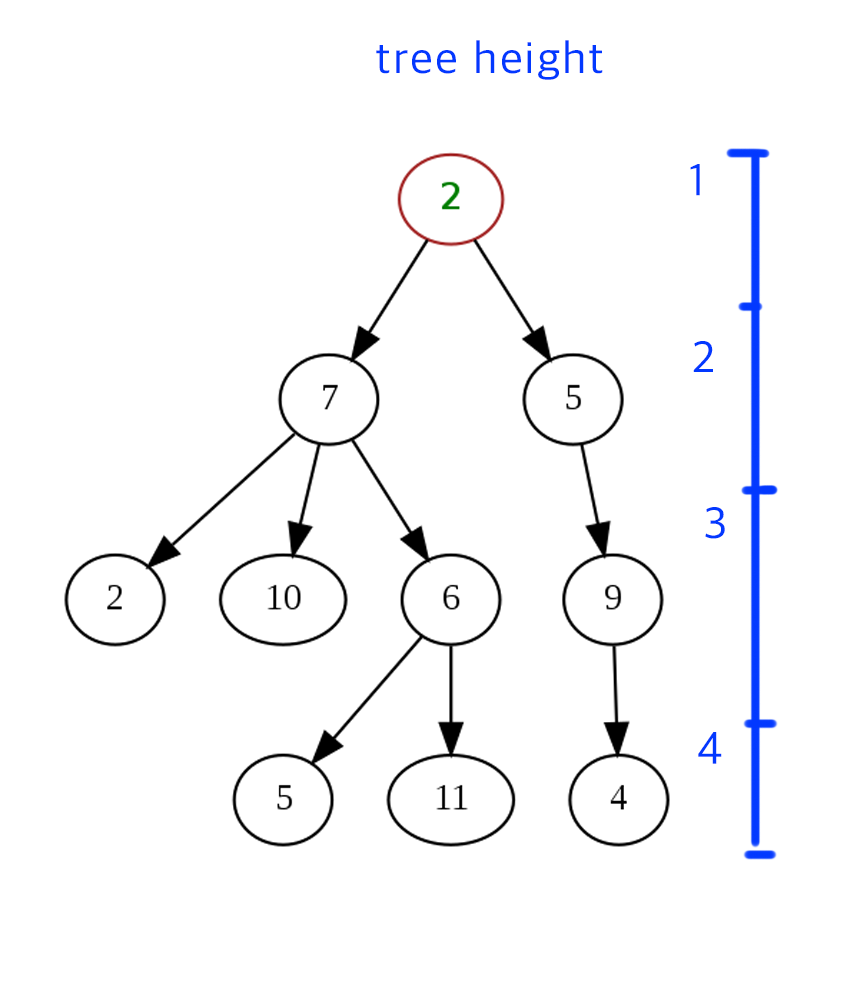
트리의 깊이는 요소에서부터 시작합니다. 요소에서부터 root까지의 거리를 재는 건데요, 9번 노드의 깊이는 3이 됩니다.

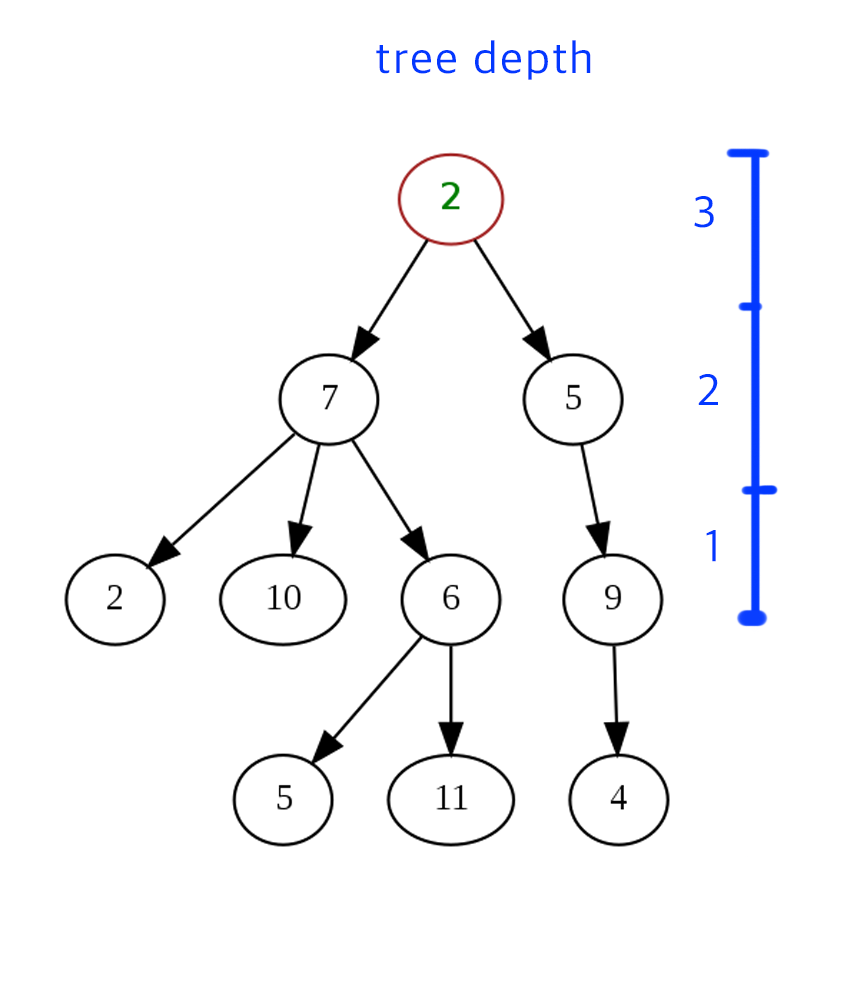
정확히는 트리 안에서의 특정 노드의 깊이라고 말할 수 있겠네요.

깊이 우선 탐색과 너비 우선 탐색

트리의 종류와 탐색 방법에 앞서, 그래프의 탐색 방법에 대해서 정리해 봅니다.
그래프의 탐색 방법에는 크게 두 가지가 있습니다. 깊이 우선 탐색 방법과 너비 우선 탐색 방법입니다.

(너무 유익하게 보았던 유튜브 추천합니다!)

깊이 우선 탐색 방법 DFS(depth-first search)

하나의 정점으로 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하고 넘어가는 방법인데요, 어떠한 방향으로 쭉 뻗어진 것을 끝까지 탐색 후, 더는 길이 없다고 생각하게 되면 다음으로 넘어갑니다. 이 방법은 '모든 노드를 돌아보고 싶을 때' 사용을 합니다. 단순 검색은 너비 우선 탐색보다 느리지만 조금 더 간단하다는 장점이 있습니다.

너비 우선 탐색 방법 BFS(Breadth-First Search)

깊이 우선 탐색 방법과 반대의 개념으로, 하나의 정점으로 시작해서 그 정점과 맞닿아 있는 가지들을 우선적으로 본 후, 그 다음 줄에 있는 가지들, 그 다음 줄에 있는 가지들을 차례대로 보는 법을 말합니다. 두 노드 사이의 최단 경로, 혹은 임의의 경로를 찾고 싶을 때 이 방법을 사용합니다.

DFS는 재귀로 움직일 수 있는 반면에 BFS는 재귀로 움직일 수 없습니다.
DFS는 스택을 사용하지만 BFS는 큐를 사용합니다.

DFS는 이진트리의 전위, 중위, 후위 탐색에 사용됩니다.

binary search tree

두 가지의 선택지밖에 없는 이진법을 지칭하는 용어의 binary와 검색을 뜻하는 search가 합쳐져 '이진 검색'을 뜻합니다. binary search tree는 이진 검색을 사용하는 트리 구조가 되겠습니다.

binary tree도 있습니다만, 그것은 BST와 살짝 다릅니다.

binary tree
각 노드가 최대 두 개의 자식을 갖는 트리입니다.
모든 트리가 binary tree는 아닙니다.

binary search tree
모든 노드가 특정 순서를 따르는 속성이 있는 이진 트리입니다.
특정 순서란? 모든 왼쪽 자식들은 root(혹은 부모)보다 작은 값이며, 모든 오른쪽 자식들은 root(혹은 부모)보다 큰 값입니다.

완전 이진 트리 VS 정 이진 트리 VS 포화 이진 트리

• 완전 이진 트리 (complete Binary Tree)
  트리의 모든 높이에서 노드가 꽉 차 있는 모든 트리를 말합니다. 마지막 노드를 제외한 모든 노드들이 두 개씩 전부 채워져 있어야 하며, 만약 하나가 비워져 있다고 하더라도 오른쪽이 비워져 있어야 합니다.

• 정 이진 트리 (full binary tree)
  모든 노드가 0개 또는 2개의 자식 노드를 가지고 있어야 합니다. 1개를 가지고 있는 것은 정 이진 트리가 아닙니다.

• 포화 이진 트리 (Perfect Binary tree)
  완전 이진 트리와 정 이진 트리를 합친 건데요, 영어를 그대로 직역한 것처럼.. Perfect, 꽉 차 있어야 되는 트리입니다. 마지막을 제외한 모든 노드가 두 개의 자식 노드를 가져야 합니다.

전위 순회, 중위 순회, 후위 순회

DFS의 기법을 따르고 있는 전위, 중위, 후위 탐색입니다.

전위 순회는 현재 노드에서 시작하여 왼쪽 노드 -> 오른쪽 노드로 갑니다.

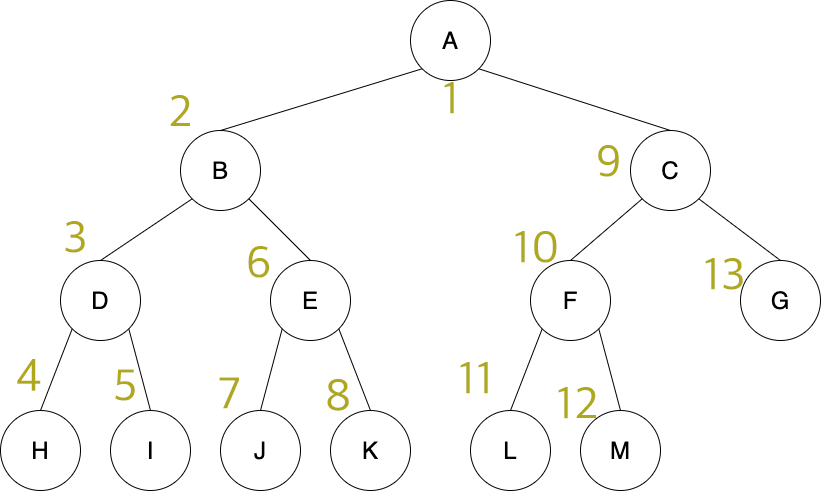
중위 순회는 왼쪽에서부터 -> 현재 -> 오른쪽 노드로 갑니다.

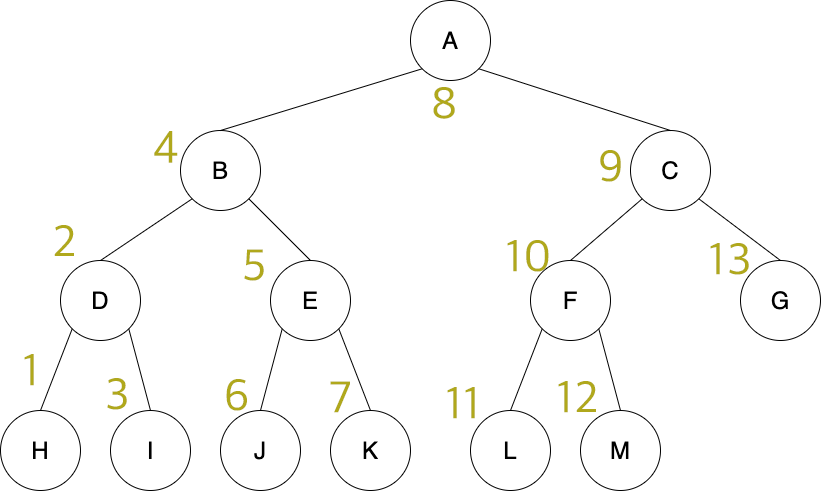
후위 순회는 왼쪽에서부터 -> 오른쪽 -> 현재로 갑니다.

즉, 현재 노드(root)가 어디에 있느냐에 따라 전위, 중위, 후휘로 나뉩니다.

tree 및 BST 구현하기

tree같은 경우는 수도 코드 없이 JS 코드만!!

//tree
class TreeNode {
  constructor(value) {
    this.value = value;
    this.children = [];
  }

  insertNode(value) {

    this.children.push(new TreeNode(value));
    return this.children;
  }

  contains(value) {


    if (this.value === value) {
      return true;
    }

    for (let i = 0; i < this.children.length; i++) {
      if (this.children[i].contains(value)) {
        return true;
      }
    }

    return false;
  }

}

tree의 contains를 구현할 때, 페어와 나의 코드가 달랐던 점이 흥미로와서 내 코드도 넣어 봤다. (과제 제출은 페어의 코드로 들어감)

contains(value) {
  let branch = this.children;
  let result = false;

  //재귀 넣기
  let again = function (branch) {
    for (let leaf of branch) {
      if (leaf["children"].length > 0) {
        again(leaf.children);
      }
      if (leaf.value === value) {
        result = true;
      }
    }
  }
  again(branch)
  return result;
}

BST 메서드

• insert: 트리에 데이터를 넣어 준다.
• contains: 트리에 해당 데이터가 있는지 알려 준다.
• inorder: 중위 순회를 이용하여 배열에 작은 값부터 큰 값을 넣는다.

BST 수도코드

• insert(value)

1. value가 root보다 작다면?
   1-1a. root의 왼쪽 노드가 없다면?
   1-1b. value를 추가한다.
   1-2a. 왼쪽 노드가 있다면?
   1-2b. 왼쪽 노드로 다시 insert를 돌린다.

2. value가 root보다 크다면?
   1-1~1-2를 오른쪽으로 변경하고 실행.

• contains(value)

0. value가 root와 같다면? -> 바로 리턴

1. value가 root보다 작다면?
   1-1. left가 없다면? -> false 리턴
   1-2. 있다면? 왼쪽 노드를 contains로 계속 돌림

2. value가 root보다 크다면?
   1-1~1-2를 오른쪽으로 변환해서 행동.

3. 그럼에도 불구하고 없다면? false

• inorder(callback)

1. 내부 함수 하나 생성.
2. 매개변수가 null이 될 때까지
3. left를 재귀
4. 해당 value를 callback에 넣음
5. right를 재귀
6. 해당 함수에 this를 넣고 리턴

JS CODE

class BinarySearchTreeNode {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
  
  insert(value) {
    if (value < this.value) {
      if(this.left === null) {
        this.left = new BinarySearchTreeNode(value)
      }
      else {
        return this.left.insert(value);
      }
    }
    
    else if(value > this.value) {
      if (this.right === null) {
        this.right = new BinarySearchTreeNode(value)
      }
      else {
        return this.right.insert(value);
      }
    }
  }
  
  contains(value) {
    if(value === this.value) {
      return true;
    }
    
    else if (value < this.value) {
      if(!this.left) {
        return false;}
      if(this.left.contains(value)) {
        return true;
      }
    }
    
    else if (value > this.value) {

      if (!this.right) {
        return false;
      }
      if (this.right.contains(value)) {
        // isContains = true;
        return true;
      }
    }
    return false;
  }
  
  inorder(callback) {
    let fn = function(node) {
      if(node !== null) {
        fn(node.left);
        callback(node.value);
        fn(node.right);
      }
    }
    return fn(this);
  }
}