마지막으로 가장 대중적이고 많이 쓰이는 SIFT 에 대해 알아보도록 하겠습니다.

Scale Invariant Feature Transform(SIFT)

지금까지 배운 것은 Feature Descriptor 로, 특징점을 기술하는 것에 그쳤습니다. 즉, 특징점의 유사도를 파악하는 것이었습니다. 그런데 특징점을 기술하기 위해서는 일단 이미지에 특징점을 찾는 detect 과정이 선행되어야 합니다. SIFT 는 feature detector 와 featue descriptor 를 모두 수행해주는 알고리즘 입니다. 이 SIFT 는 컴퓨터 비전에 본격적으로 Neural Network 가 도입되기 전에는 가장 널리 사용되었던 디스크립터로, Neural Network를 적용하기 힘든 일부 어플리케이션에서는 여전히 많이 사용되고 있습니다.

SIFT 의 Detection 에서는 다양한 크기의 주목해서 봐야할 영역을 찾고 이를 localization 와 normalzation 을 거쳐 gradient 를 써서 orientation 을 구하고 그것들을 최종적으로 고차원 vector 형태로 나타내게 됩니다.

Blob

SIFT 를 배우기 전 우리는 먼저 Blob 에 대해서 알아야 합니다.

Blob 이란 밝기나 색상이 매우 일정한 이미지의 영역을 의미합니다.

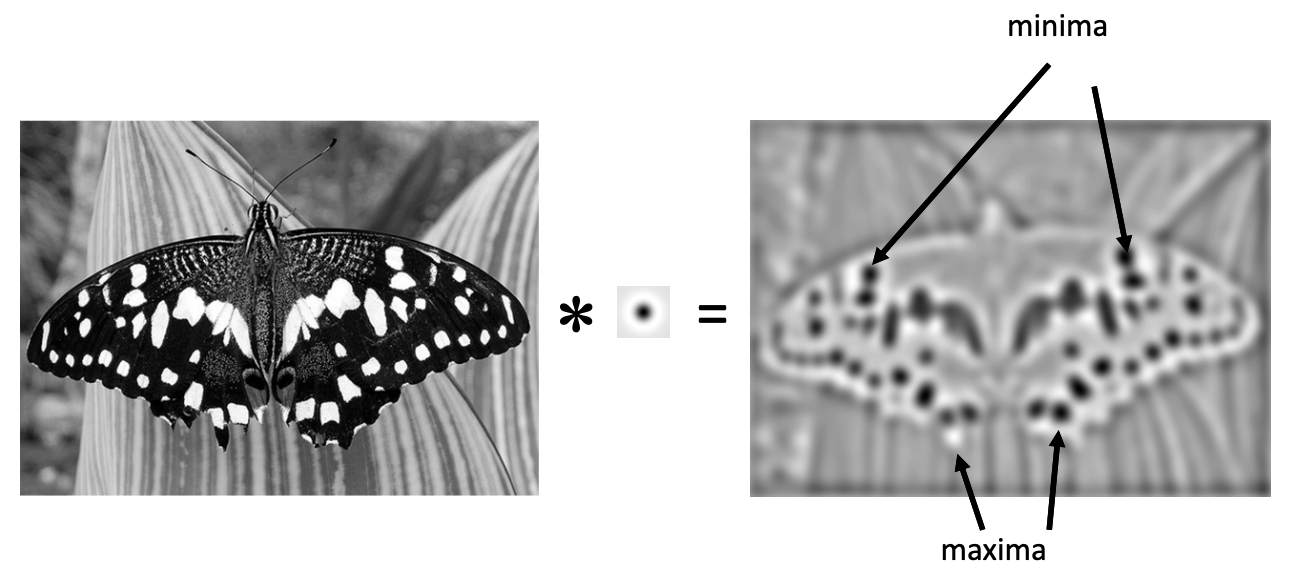
위와 같이 해바라기들이 즐비한 두 이미지가 있습니다. 해바라기 중심의 동그란 영역은 색과 밝기가 매우 일정합니다. 이 곳이 대표적인 Blob 이 되는 것입니다. 그렇기 때문에 이 Blob을 찾는 Blob detection 은 이미지에서 밝기나 색상 같은 여러 특징들이 주변과 다른 영역을 찾으면 되는 겁니다.

그렇기 때문에 만약 우리가 동그라미 모양의 Blob 을 찾고 싶다면 Blob Filter는 위의 오른쪽과 같은 모양을 합니다. (예를 들어 별 모양이면 별 모양의 검정 주변에 하얗게 생긴 모습이겠네요.)중앙의 원 부분이 주변과 값의 차이를 크게 띄고 있습니다. 검정색은 값이 매우 작은 부분이고 겉의 흰 색은 값이 매우 큰 부분이지만 당연히 반대도 가능하겠습니다.

이 값이 의미있으려면 이미지는 어떻해야 할까요? 값이 작은 검정 영역에 해당하는 픽셀들이 값이 작고 값이 큰 흰색 영역에 해당하는 픽셀들이 값이 크다면 필터를 적용한 값이 클 것입니다. 아니면 반대인 경우에 필터를 적용한 값이 작을 것입니다. 값이 많이 크거나 많이 작은 경우, 즉 이 필터와 흡사한 경우에 response 가 큰 것이 되는 겁니다.

이 필터의 크기를 다양하게 해 Blob을 찾아낸 결과가 왼쪽 그림과 같은 것입니다. 결과를 픽셀 값으로 표현한 예시는 아래와 같습니다.

그런데 이렇게 다양한 크기로 필터를 적용해야 할 때, 우리는 이러한 두 가지 방식 중에 고민할 수 있습니다. 이미지의 크기는 고정하고 필터의 크기를 바꿔가면서 필터링을 수행하는 것이 더 좋을지, 반대로 필터의 크기를 고정하고 이미지의 크기를 바꿔가며 필터링을 하는 것이 더 좋을지 말입니다. 정답은 후자입니다. 왜냐하면 둘다 똑같은 만큼 수행하지만 이미지가 작아질수록 그 필터가 차지하는 영역이 커지기 때문에 필터링에 걸리는 시간이 줄어들기 때문입니다.😁 다만 이미지를 줄이는 것은 언제나 정보 손실에 유의해야 하겠죠?

근데 여기서 또 정말 신기한 것이 우리가 적용하고자 하는 이 Blob Filter 가 실제로는 Laplacian 과 거의 흡사한 것입니다!

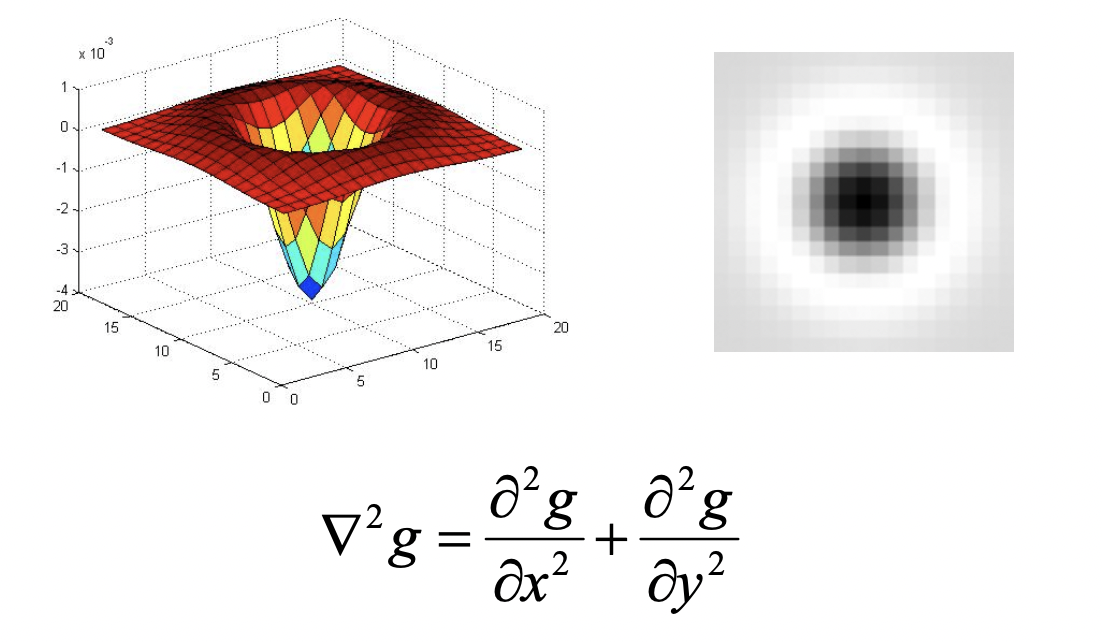
그래서 우리는 Laplacian 을 활용할 것입니다. 그런데 이미 말씀드린 문제가 있습니다. 아래는 다양한 픽셀을 가지는 이미지에 $\sigma = 1$ 인 Laplacian 을 적용한 예시입니다. $\sigma$ 값이 작기 때문에 가장 오른쪽의 굉장히 작은 Blob 에만 알맞게 반응합니다. 그리고 이보다 큰 Blob 에서는 edge 에만 살짝 반응하고 마는 것입니다. 상상해보면 이해가 되죠?😅

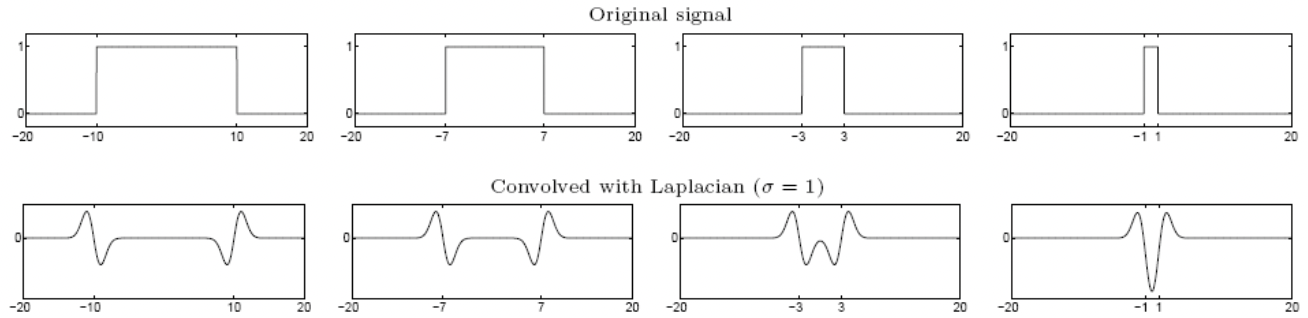
즉, Laplacian의 크기와 Blob의 크기가 매치해야지만 훌륭한 response를 보인다는 것입니다.

아래 예시들을 보겠습니다.

위와 같이 같은 해바라기 이미지지만 왼쪽은 원본 사이즈이고, 오른쪽은 3/4 크기로 조금 작습니다. 여기에 $\sigma = 2.1$ 인 필터를 적용해봅시다.

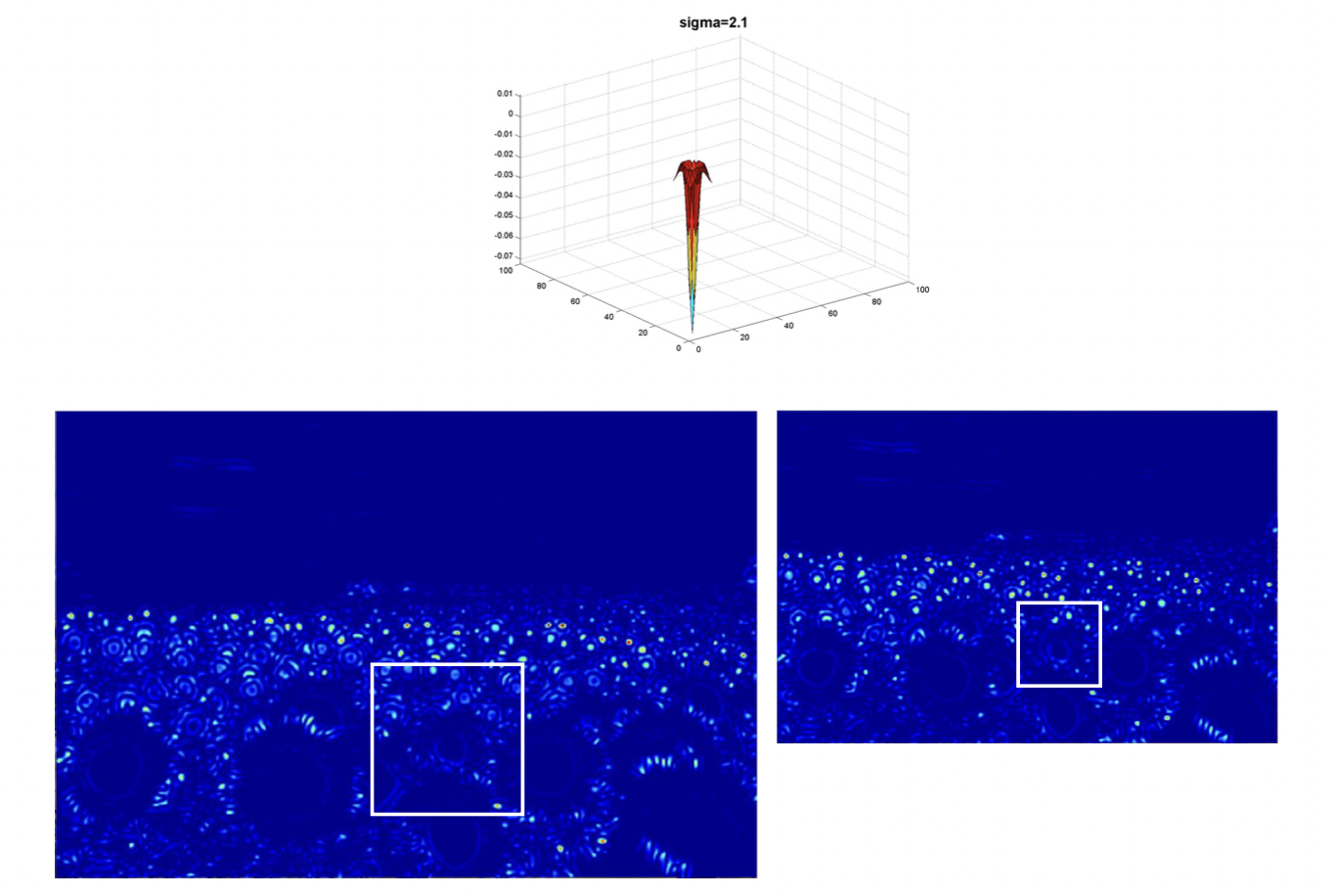
헷갈리시면 안되는 게 흰색 박스는 필터가 아니라 같은 영역을 비교하기 위함입니다. 당연히 필터의 크기는 같겠지요. 그런데 비교해보시면 $\sigma$ 값이 작기 때문에 오른쪽에서 잡힌 작은 Blob들(박스 내 오른쪽 위)이 왼쪽에서는 잡히지 않은 것을 볼 수 있습니다. 그 Blob 들은 필터에 비해 커서 그렇겠네요. (크다고 표현하는 것은 필터 자체의 크기가 아니라 필터 안의 'blob' 모양의 크기인 거 아시죠??😁)

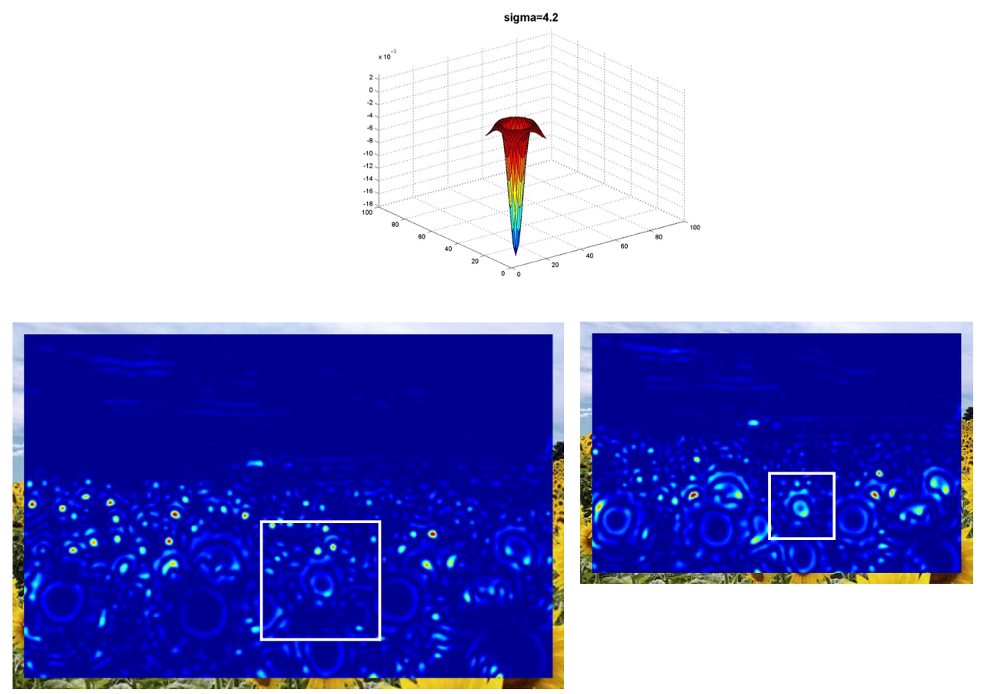
$\sigma = 4.2$ 로 두 배를 키워보니 이제 오른쪽에는 더 큰 크기의 Blob 도 잡히기 시작합니다. 이전에 잡혔던 작은 Blob 들은 이제 필터보다 사이즈가 작아져서 response도 작아자기 때문에 옅어진 것을 확인할 수 있습니다.

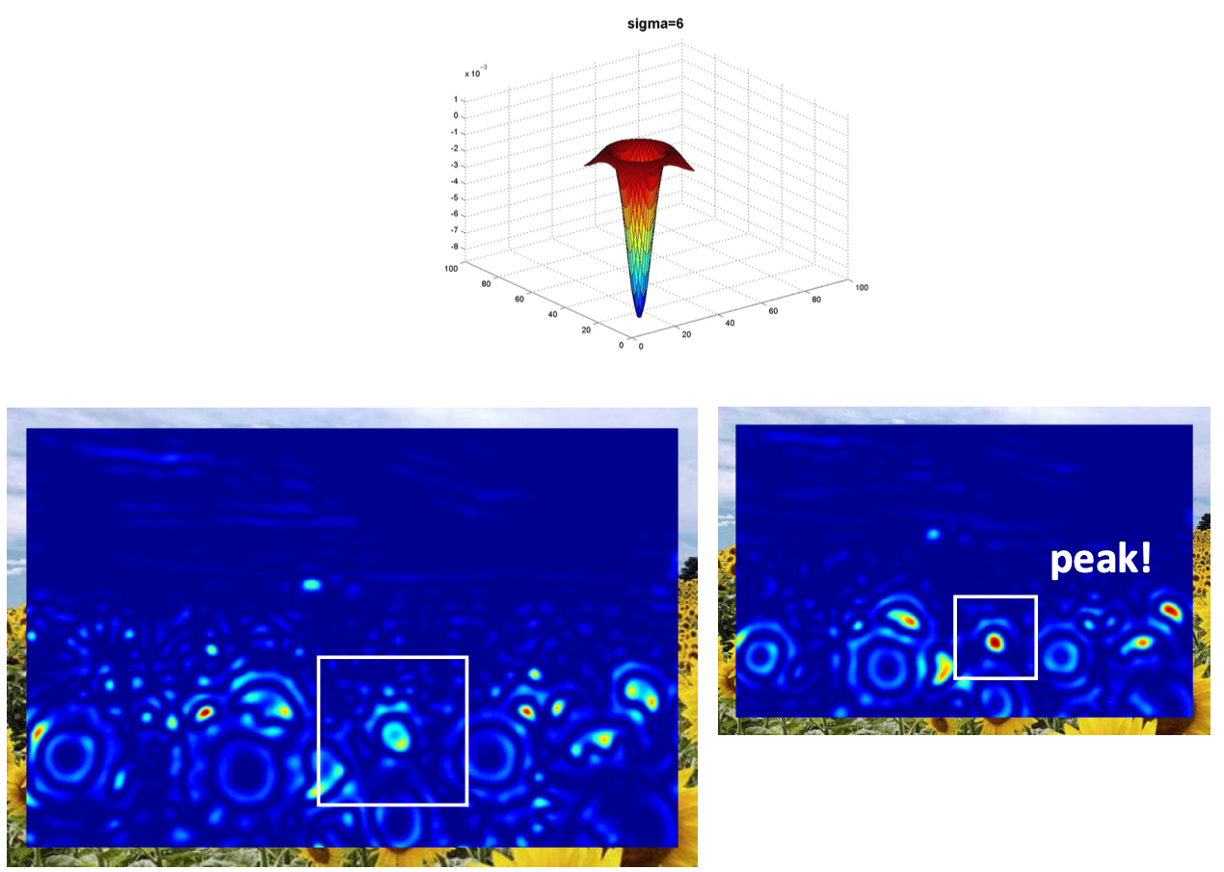
$\sigma = 6$ 으로 하니 오른쪽의 Blob 과 사이즈가 딱 맞나 봅니다. 피크를 찍었네요. 왼쪽의 큰 Blob 도 스멀스멀 잡히기 시작하는 것 같습니다.

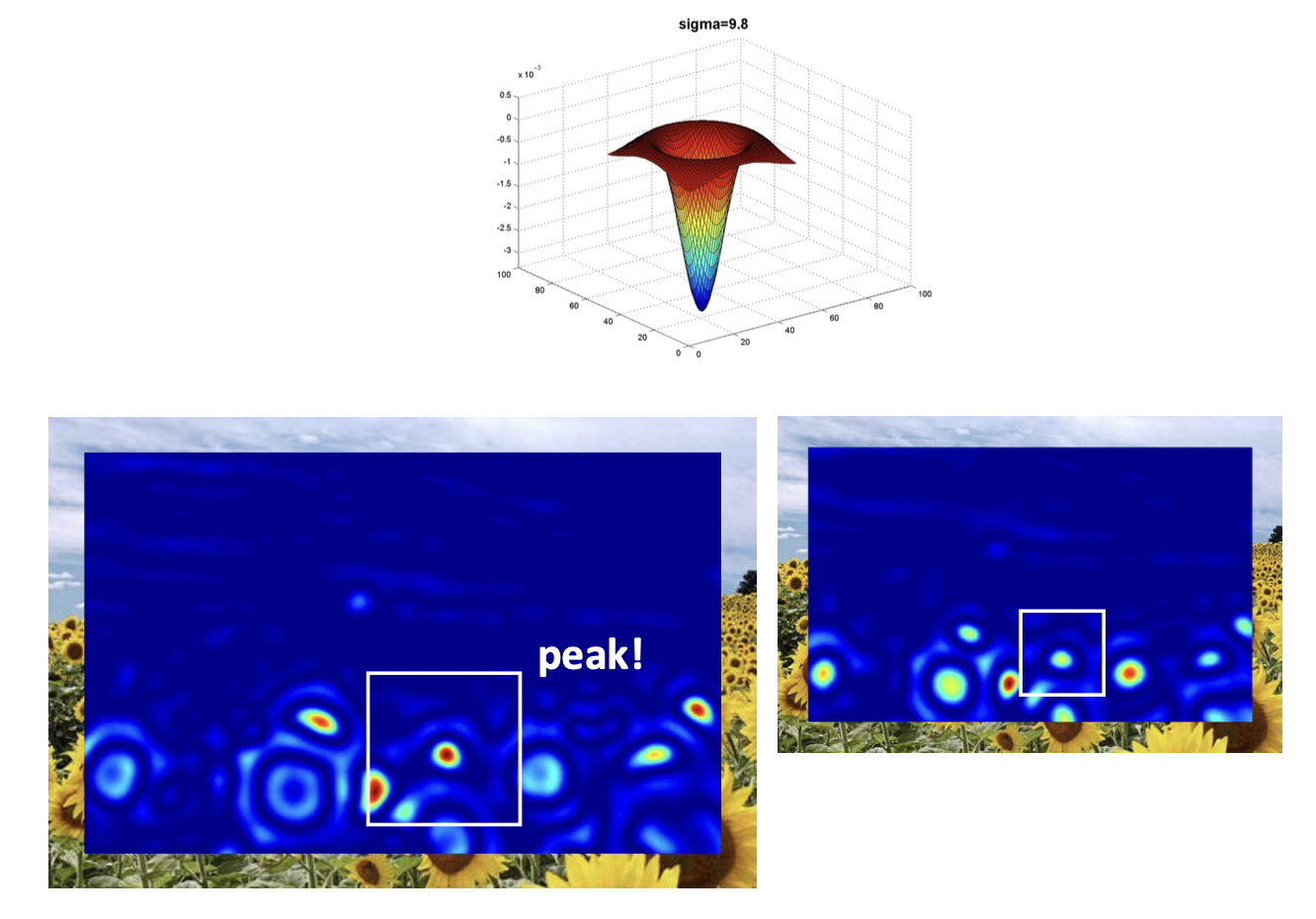
$\sigma = 9.8$니 비로소 왼쪽의 Blob 가 크기가 매칭됬나 봅니다. 반면 오른쪽 이미지에서는 이제 필터가 너무 커져서 희미해지고 있습니다.

그 이후로 키우는 것은 이제 두 이미지 입장에서도 모두 커서 점점 더 아무 Blob 도 잡지 못하게 되는 것을 확인할 수 있습니다. 결론적으로 여러 $\sigma$ 를 적용해 보았을 때의 이미지 크기에 따른 결과는 아래와 같습니다.

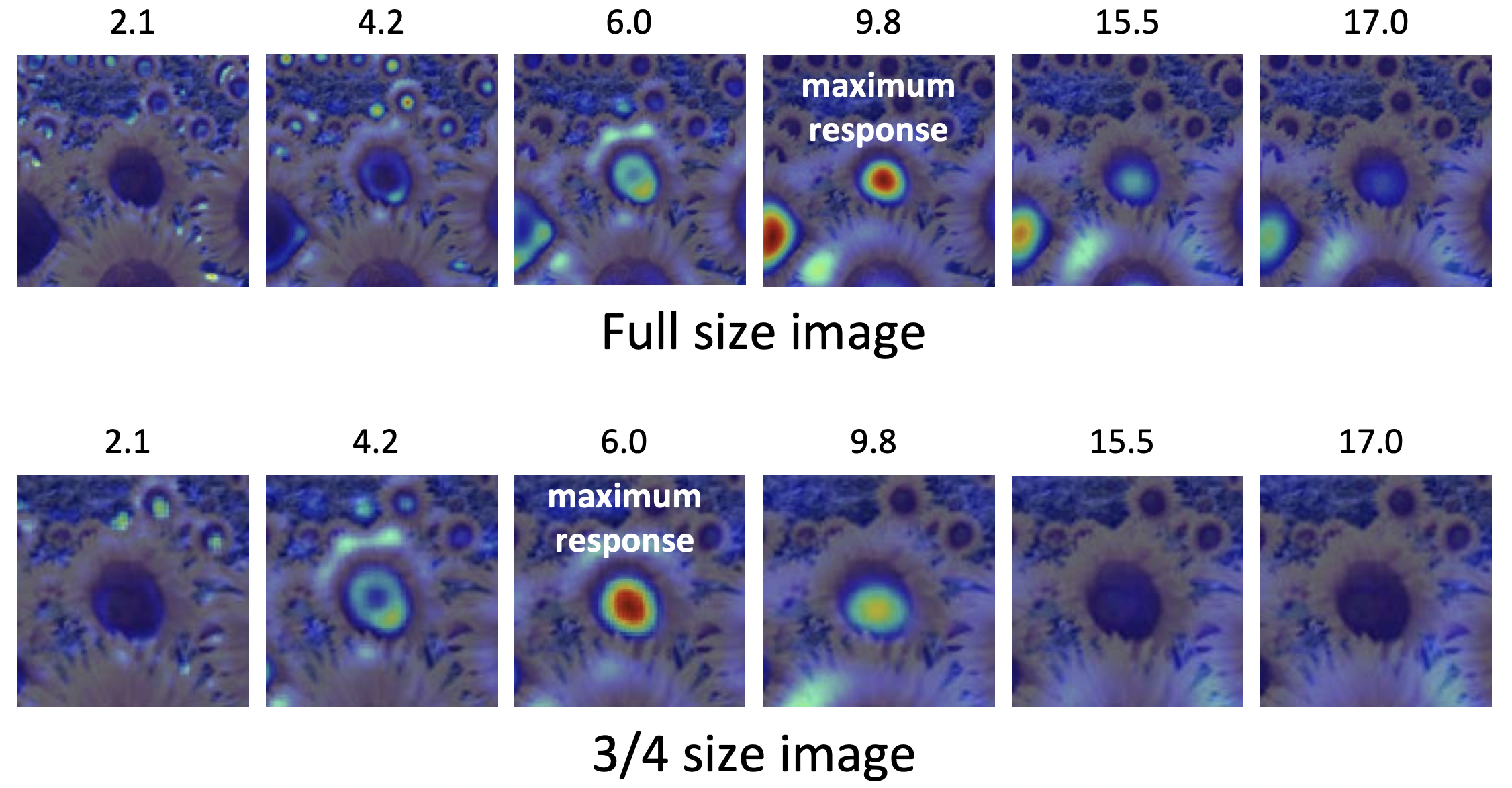
원본에서는 9.8 정도에 최대의 response 값이 나오게 되었고 3/4 이미지에서는 9.8의 3/4 정도인 6.0에서 최대의 response 값이 나왔습니다. 즉 이미지마다 최대의 response를 갖는 paremeter 값이 다르기 때문에 우리는 여러 스케일의 Laplacian 을 적용해 봄으로써 고유의 Characteristic Scale 을 찾는 것이 목표입니다.

그런데 여기서 우리가 생각해봐야 할 문제가 있습니다. 아래 그림으로 Laplacian 을 다시 봅시다. $\sigma$ 값이 커질수록 값이 더 퍼지는 경향이 있습니다. 그래서 값 자체만 놓고 본다면 그냥 무조건 $\sigma$ 가 작을 수록 값이 절대값이 더 크다는 것입니다.

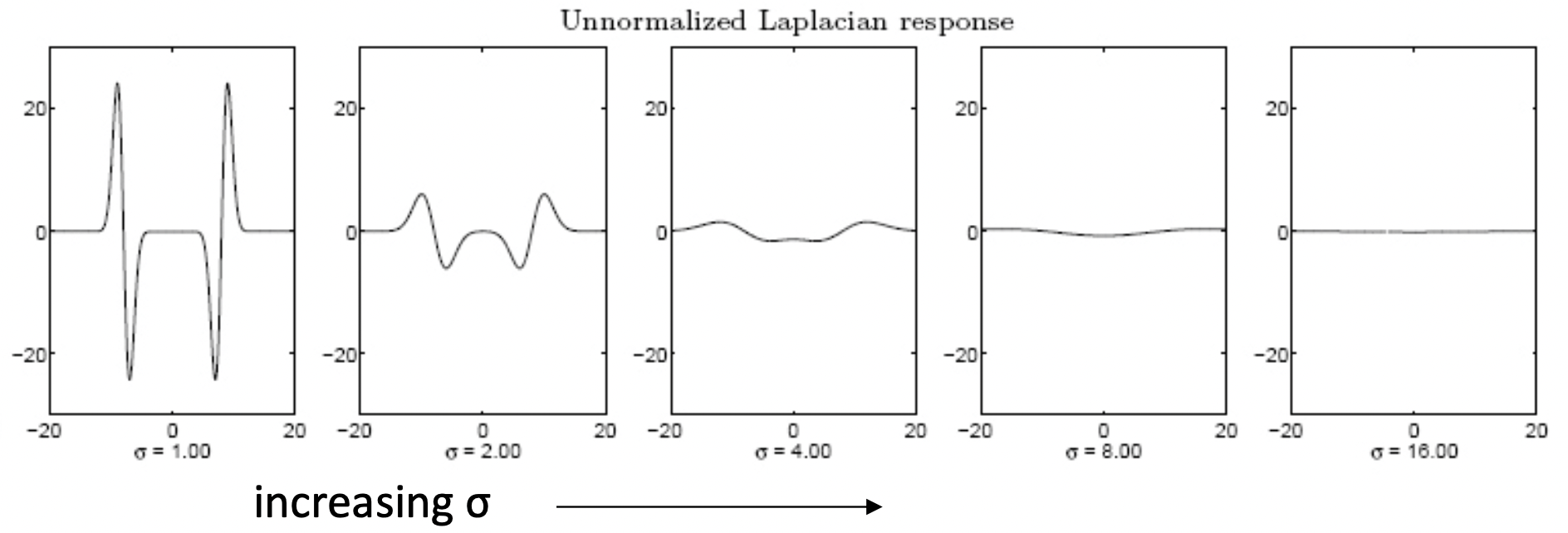
그래서 사실 더 큰 $\sigma$ 에서 Blob 과 스케일이 맞아 response 값이 가장 최대가 되어야 하는 이미지에서도 작은 $\sigma$ 와 값 자체를 비교하면 response 값이 더 작을 수도 있다는 얘기가 됩니다. 이것은 Laplacian 자체는 아직 Unnormalized 기 때문이죠. 이를 Normalization 해주기 위해 먼저 가우시안을 미분한 함수의 예시를 들어봅시다.

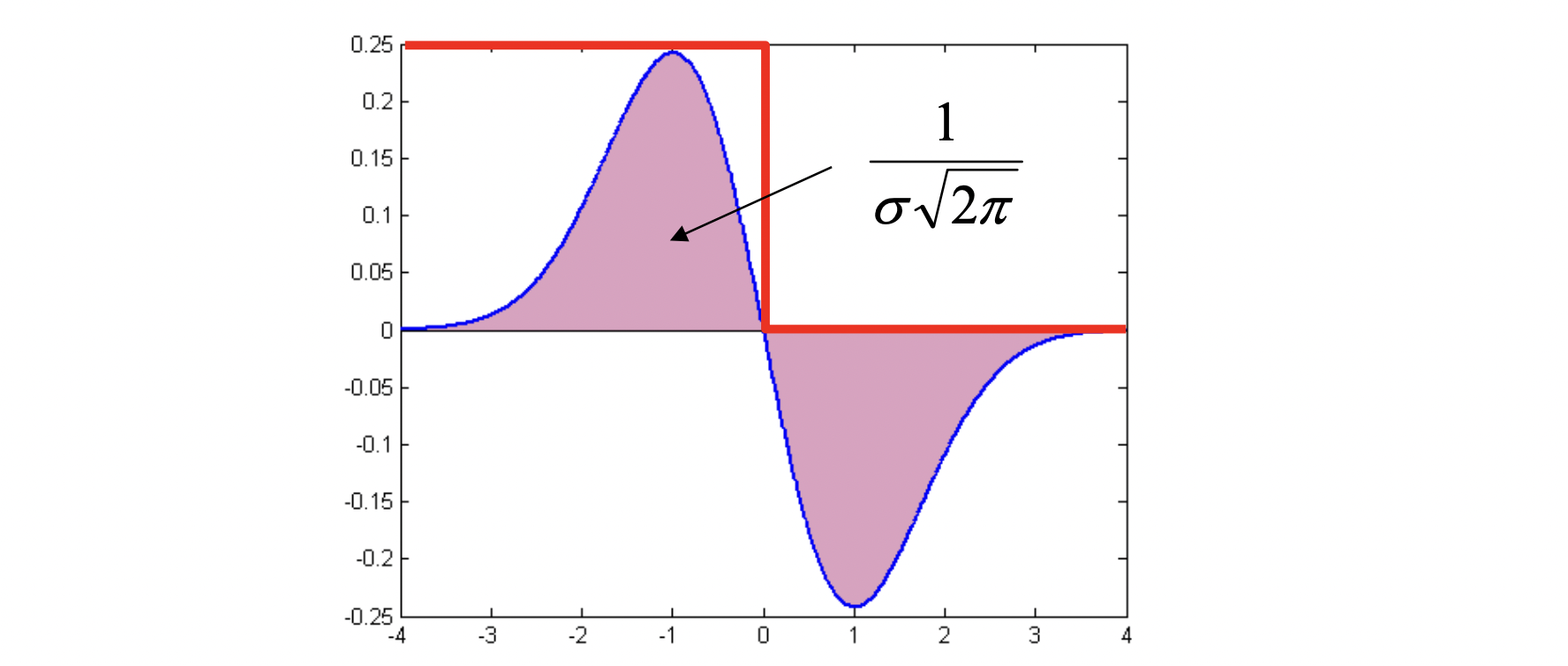
빨간색은 이미지의 Intensity 입니다. 우리가 response 를 구하는 방식은 Intensity 범위 내에서 즉, Intensity 값을 포함하는 derivative of Gaussian 필터의 넓이를 구하는 것입니다. 즉 적분을 하는 것이죠. 그런데 실제로 derivative of Gaussian 을 적분한 값은 위에서 확인 가능하듯이 $\frac{1}{\sigma\sqrt{2\pi}}$ 입니다. 그렇기 떄문에 $\sigma$ 값이 커질수록 해당하는 reponse 값도 작아진 것입니다. 그렇다면 이를 Normalization 하는 것은 간단합니다. 그냥 $\sigma$ 를 곱해주면 되겠지요? 그러면 $\sigma$ 값에 상관없이 항상 해당하는 너비는 $\frac{1}{\sqrt{2\pi}}$ 가 될테니까요! 그러면 Gaussian 을 두 번 미분한 second derivative of Gaussian 인 Laplacian 함수는 당연히 어떻게 하면 될까요?

$\sigma^2$ 를 곱해주면 되는 겁니다!

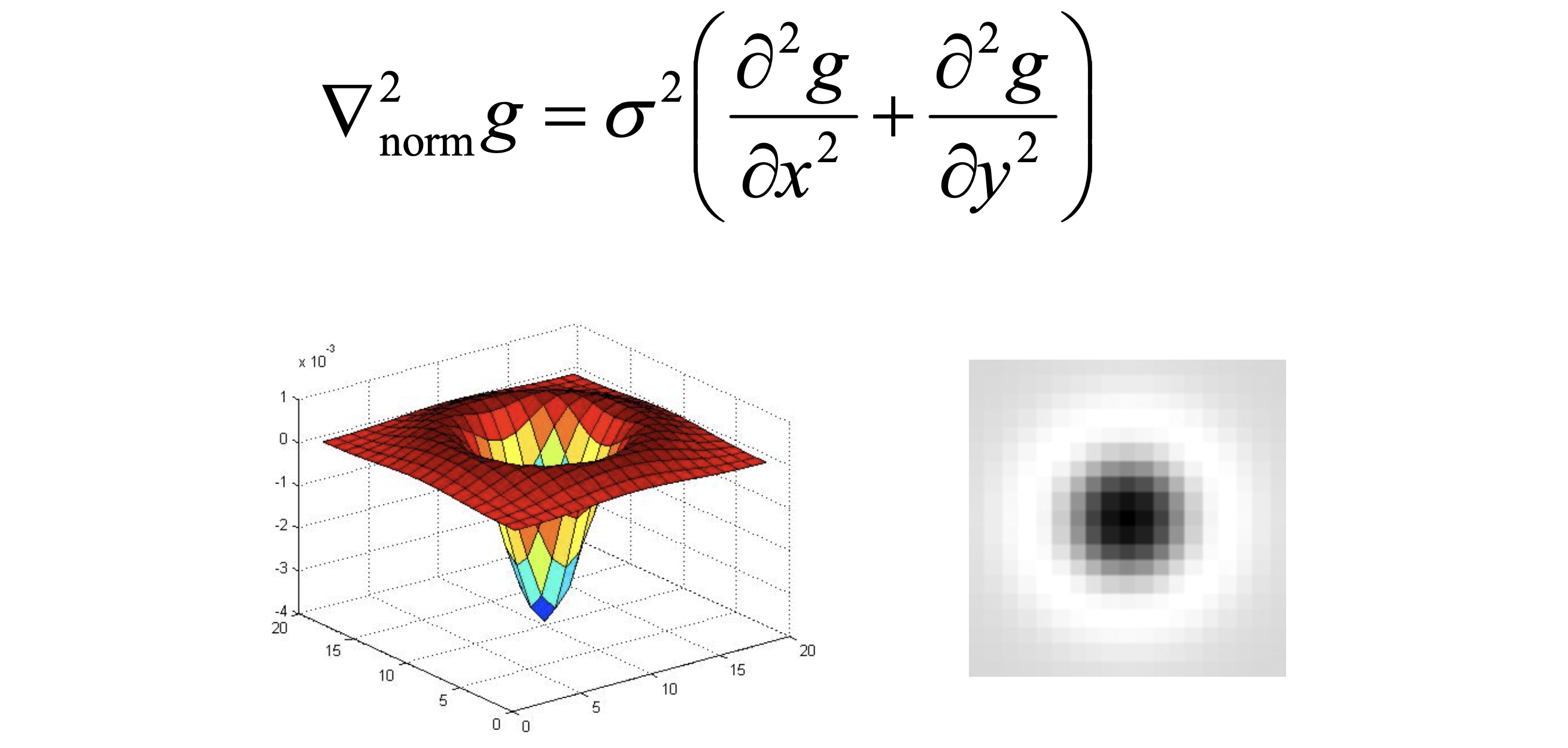
그래서 최종적으로 Normalization까지 마친 Scale-normalized Laplacian 즉, 우리의 Blob Filter 는 위와 같은 수식과 모양을 가지게 되는 것이죠. 그렇다면 이제 어떤 scale 일 때 반지름이 $r$ 인 원 (Blob) 이 최대의 response 를 가지게 될까요? 직관적으로 생각하면 Laplacian Filter 의 가운데 검정 동그라미가 원과 크기가 정확히 일치할 때가 될 겁니다. 이를 픽셀 세기로 표현한 1차원 그래프는 아래와 같습니다.

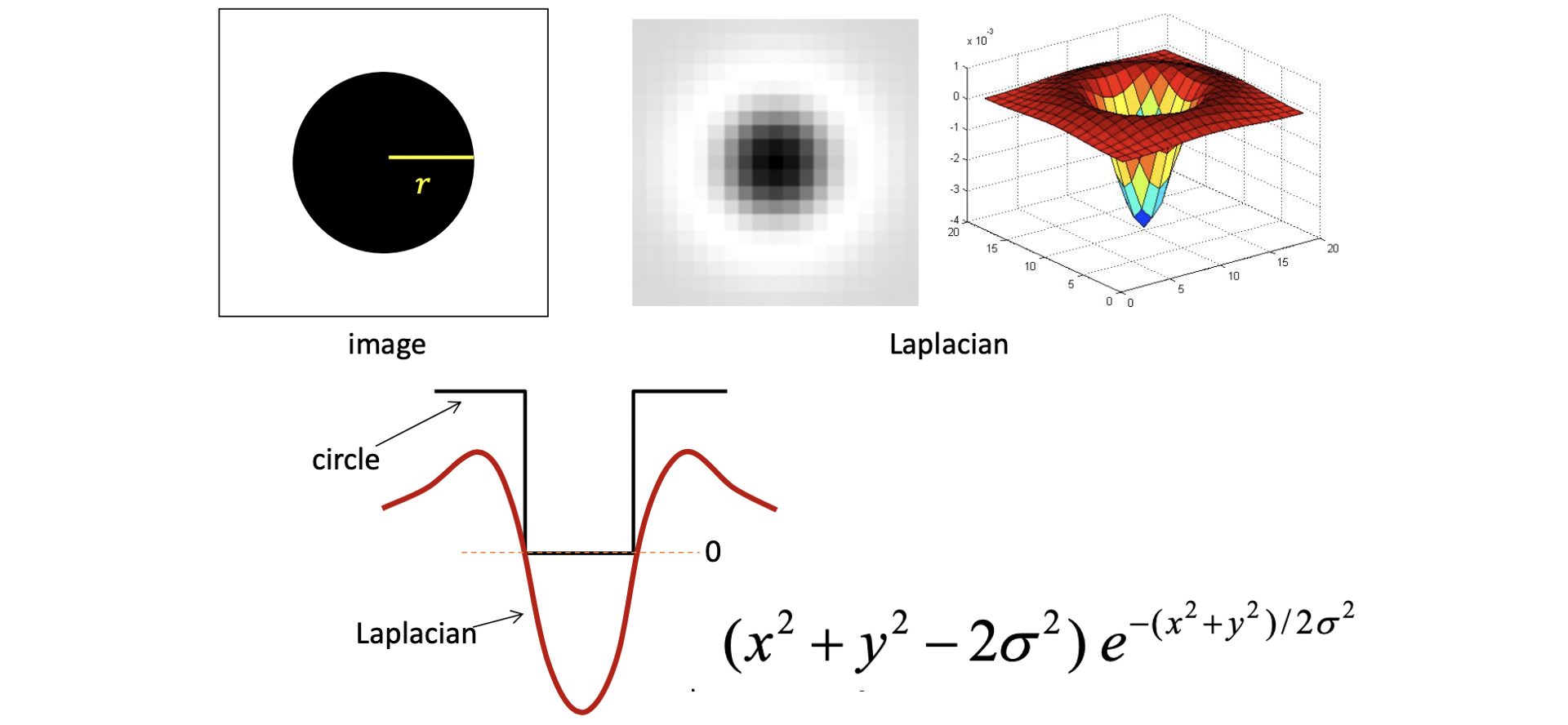
Laplacian 이 0을 지나는, 즉 색이 바뀌는 점과 점 사이에 동그라미가 일치해야 합니다. 여기서 Laplacin의 식은 위와 같습니다. Laplacian 값이 0인 점 사이의 거리가 원주인 $2r$ 이 되어야 하기 때문에, 즉 $x^2 + y^2 = r^2$ 일 때 0이어야 하므로 $(r^2 - 2\sigma^2)e^{-\frac{r^2}{2\sigma^2}} = 0$ 이 되고 이를 풀면 아래와 같은 결과가 도출됩니다.

$\sigma = r / \sqrt{2}$ 일 때 최대의 response 를 보인다.

이를 알고 이제 진짜 detection 으로 들어가봅시다. 먼저 어떤 이미지에 여러 $\sigma$ 값들로 여러 장의 reponse 값을 출력합니다. 픽셀에 대한 여러 reponse 값들 중 최대인 하나를 선정하는 작업은 아래와 같습니다.

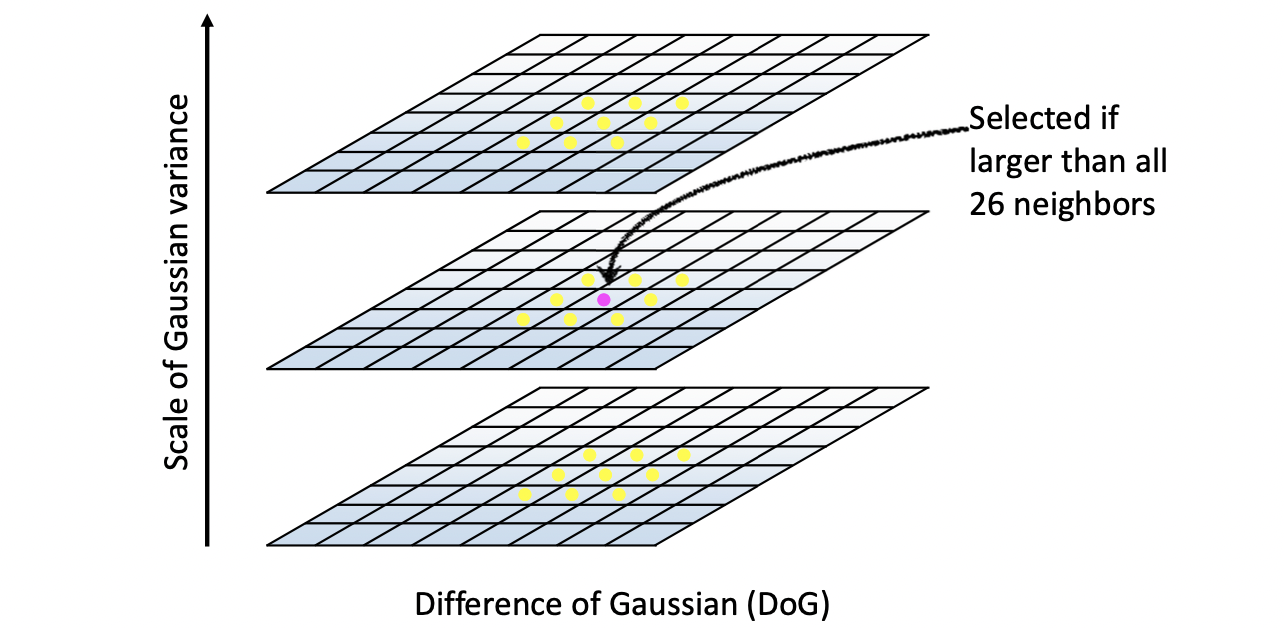
먼저 response 값을 제곱합니다. 최대의 response를 하면 Filter와 정반대 강도의 Blob 은 음으로 가장 큰 값을 가질테니 절대값을 위해 제곱을 하는 겁니다. 이후, 어떤 $\sigma_i$ 에 대한 reponse 가 있을 때 그것보다 한 단계 작은 그리고 한 단계 큰 $\sigma$ 값에 대한 reponse 까지 가져옵니다. 여기서 자신을 포함한 주변 8개의 이웃값들과 $\sigma_i$ 에서의 이웃값들 총 9 + 8 + 9 = 26 개의 값들 중 자신이 가장 크다면 그 픽셀 값은 $\sigma_i$ 에서 가장 큰 response 가지는 값이 되는 겁니다. $\sigma$ 를 아니 원에 대한 반지름 $r$ 도 알 수 있기 때문에 이를 원으로 표시하며 전체 픽셀을 다 수행한 결과는 아래와 같이 나오게 되는 겁니다.

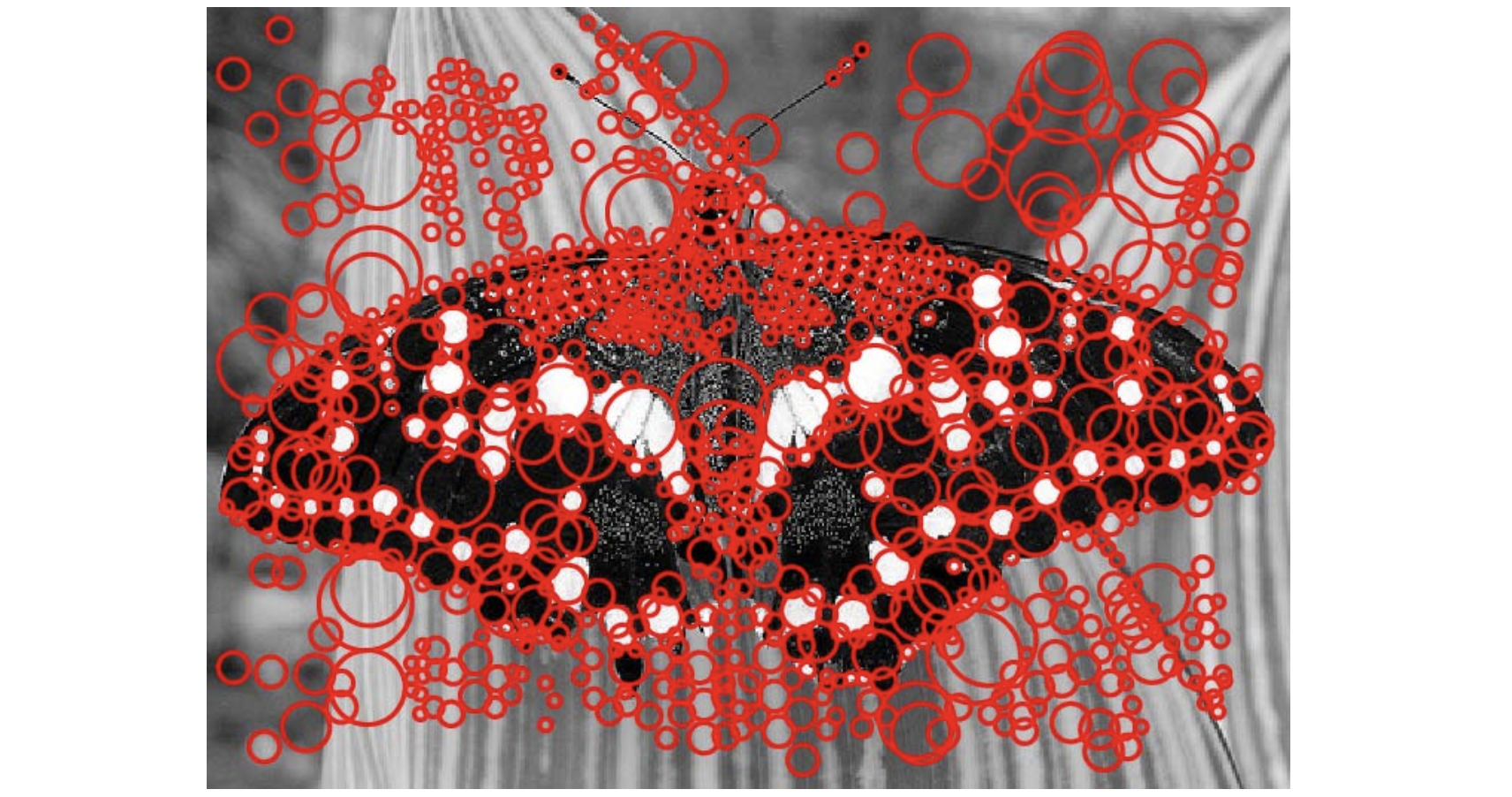
이와 같은 과정은 이미지의 컨텐츠를 이해하거나 다른 이미지와 비교할 때 굉장히 중요한 역할을 하는 Blob 영역, 즉 feature 를 찾는 detection 과정이 됩니다. 하지만 Laplacian 은 Guassian 을 두 번 미분하는 만큼 계산에 부담이 되지 않을 수 없습니다. 따라서 우리는 아래와 같이 Laplacian 대신 Difference of Gaussians(DOG) 로 Laplacian 을 approximation 해서 사용하려 합니다.

$\sigma$ 가 큰 Gaussian은 낮고 퍼져있는 형태인데 이 값에 $\sigma$ 가 작아 높고 좁혀져 있는 값을 빼면 위와 같은 모양이 나오는 것입니다. 하물며 runtime 때 일일히 미분을 해야하는 Laplacian 과 달리 DOG 를 사용하면 Gaussian 값을 재활용 할수도 있다는 장점이 있는 것이죠.

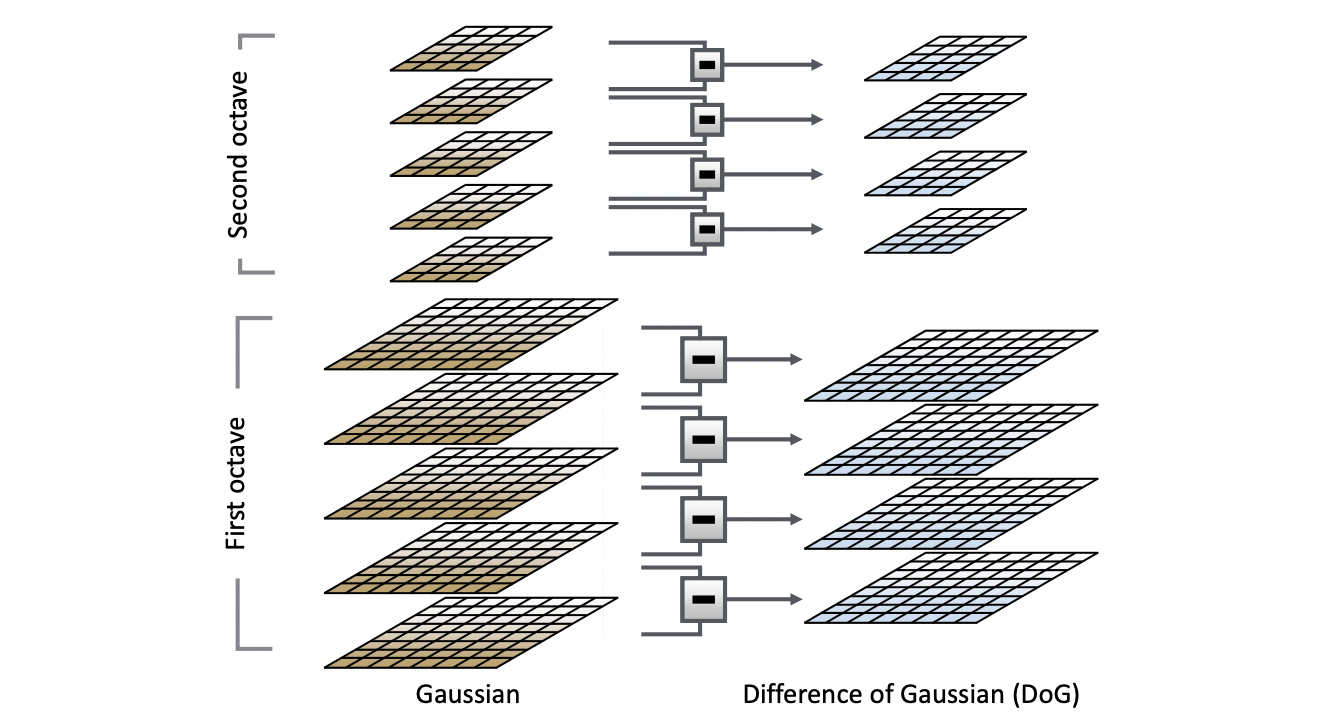
따라서 SIFT 의 실질적인 구현은 위와 같이 일어납니다. 여러 $\sigma$, 즉 여러 Scale 을 가지는 Gaussian 값들에 대해서 이웃한 것들을 빼면 그 결과는 여러 $\sigma$, 즉 여러 Scale 을 가지는 DOG 를 Laplacian 의 근사치로써 구할 수 있는 것입니다.

그런데 한 가지 문제가 더 있습니다. DOG response 로 구한 값이 Blob 이 아닌 edge 에서도 굉장히 크게 나온다는 것입니다.(Laplacian 도 마찬가지입니다.) 그래서 우리는 Harris Response Function 을 통해서 edge 에 해당하는 부분들을 지울 겁니다. (Corner Detection 에서 봤던 그 Harris 맞습니다.😊)

이렇게 되면 여기까지가 어떻게 SIFT 에서 중요하게 생각하는 features, 즉 Blob 들을 찾아낼 것인가에 대한 이야기였습니다. 그러면 이제는 어떻게 이 영역들을 수치적으로 표현할 것인가에 대한 이야기를 해보겠습니다.

위와 같이 서로 같은 곳을 서로 다른 scale 과 각도로 찍은 예시가 있습니다. 따라서 우리가 이미지의 어떤 영역을 비교하기 위해서는 같은 크기, 같은 각도로 바꿔주는 Normalization 이 필요합니다.

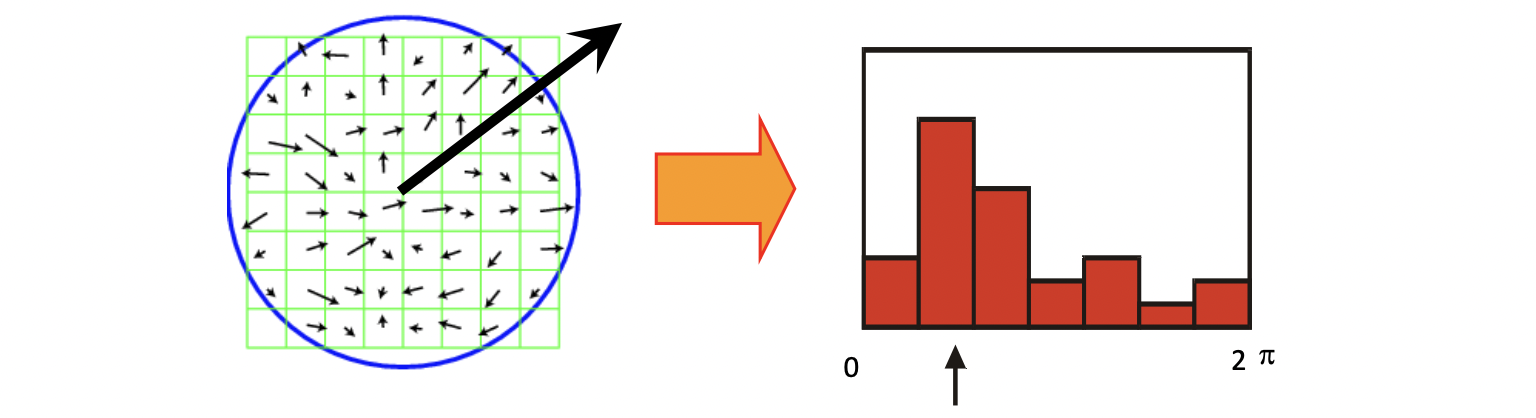
Reference Orientation 은 이미 한 번 언급 했지만 왼쪽과 같이 이미지 영역에서의 Image Gradient 들을 오른쪽과 같이 히스토그램으로 나타내어 가장 dominant 한 방향을 기준으로 이미지를 돌려주는 것입니다.

이렇게 SIFT 로 feature 들을 추출한 결과는 위와 같습니다. 또한 SIFT 는 다음과 같은 두 가지 목표를 가집니다.

1. Detection is covariant
   $features(transform(image))=transform(features(image))$
2. Description is invariant
   $features(transform(image))=features(image)$

이 조건들이 충족 됐을 때 비로소 좋은 Feature Descriptor 라고 부를 수 있는 것이지요.

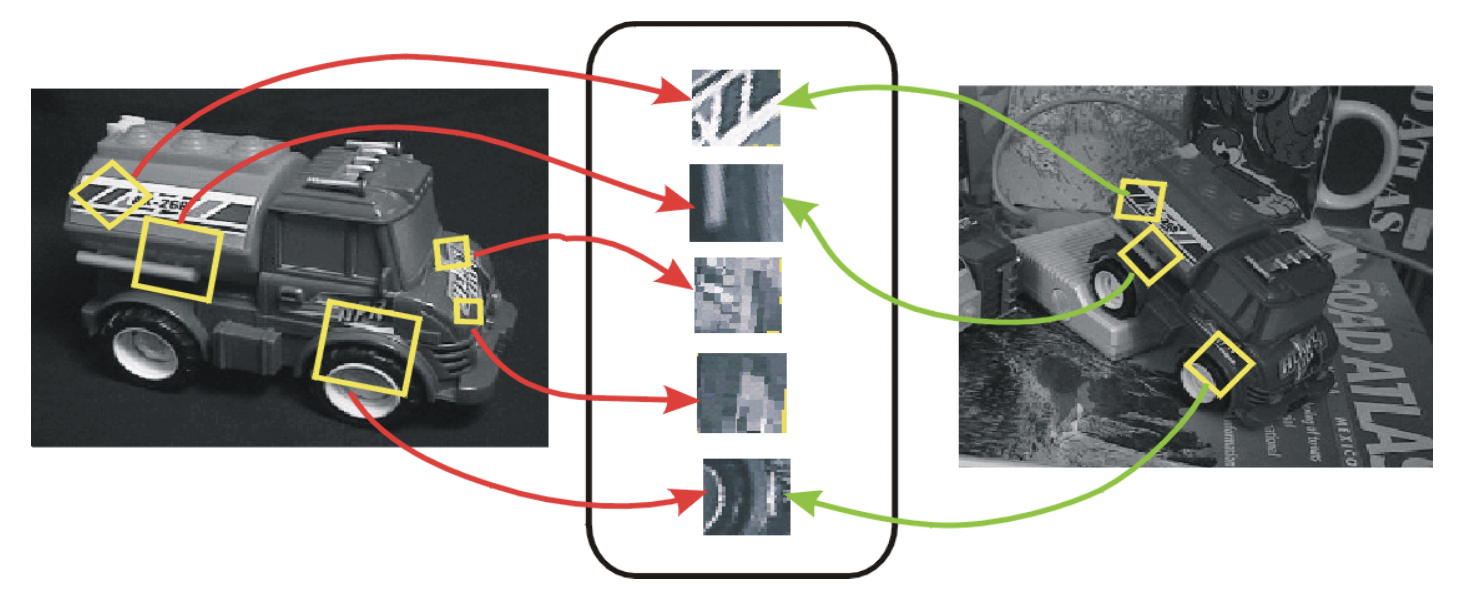
따라서 위 그림과 같이 transform 되어 있는 같은 장난감 이미지에서 뽑은 feature 들이 잘 매칭되게끔 하는 것입니다.

부가적으로 SIFT 의 아이디어는 아래와 같습니다.

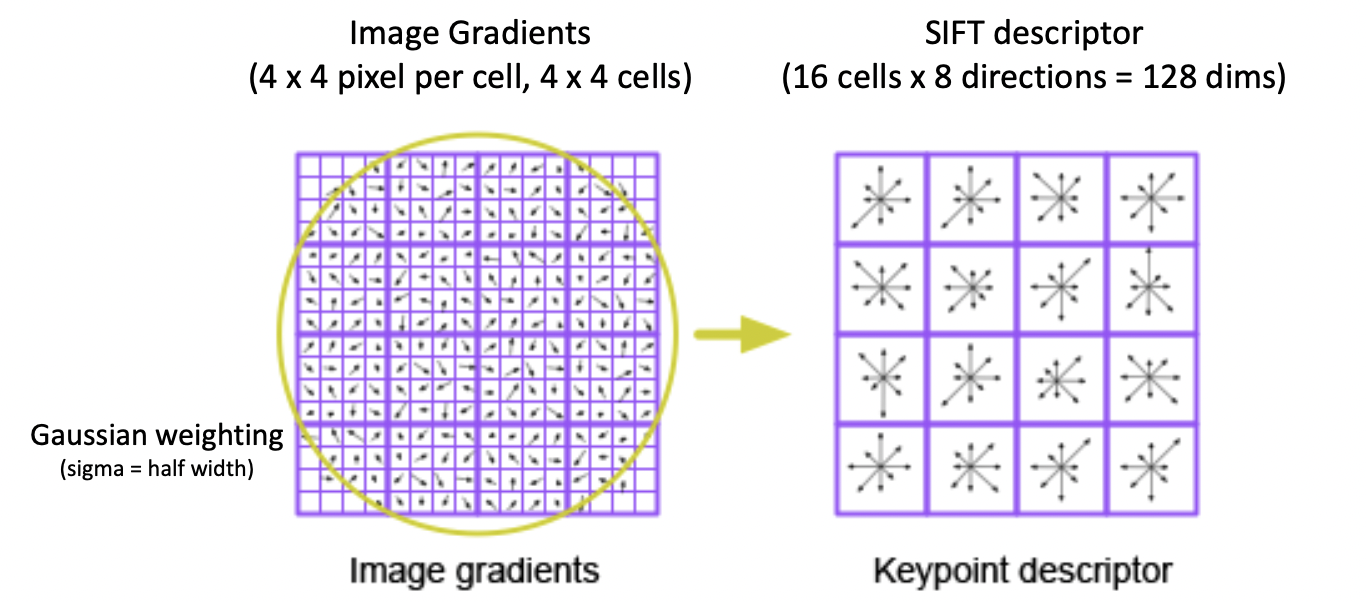
우리가 찾은 Blob 에 대한 이미지 패치가 위와 같이 있습니다. Normalization을 거친 기준이 되는 크기는 16 X 16 픽셀입니다. 모든 픽셀에는 각각 image gradient 값이 계산되어 있습니다. 이 gradient 값에 대해서 패치 너비의 반이 $\sigma$ 값을 가지게끔 패치의 중앙이 가장 크게 반영되는 Gaussian Weighting 을 수행합니다. 그리고 각각을 4 X 4 픽셀 크기의 16개의 셀로 구분합니다. 그리고 이들을 8개의 방향에 대해서 인코딩을 해서 히스토그램처럼 나타내면 16개의 셀에 대해 8개의 방향이므로 총 128개의 값이 도출되게 됩니다. 이를 나열한 것이 바로 SIFT Descriptor 가 비교하는 최종 값이 됩니다.

이와 같은 SIFT 는 시점과 조명 변화에 강하며, DOG 를 도입한 것 처럼 굉장히 효율적으로 구현이 용이합니다. 빠르고 효율적이라 real-time 으로도 동작 가능할 뿐 아니라 많은 소스 코드들이 세상에 존재합니다. 이와 같은 강력한 장점들로 Neural Network 가 도입되기 전 가장 강력한 Descriptor 중에 하나였던 겁니다.☺️