이미지에서 특징점을 기술하는 것이 어떤 방식으로 이루어지는지 알아보도록 합시다. 먼저 이와 같은 과정이 왜 필요할까요?

두 사진을 보면 우리는 본능적으로 같은 벽면을 찍었다는 것을 알 수 있습니다. 그치만 다른 시점에서 찍혔기 때문에 픽셀 값 자체에는 변형이 일어났죠. 이 때 컴퓨터는 이 두 이미지가 같은 물체에 해당하는 지를 파악하기 위해 특징점을 비교해야 합니다.

왼쪽을 보면 같은 책이지만 다른 조명 값 때문에 색깔이 달라서 픽셀 값만을 보는 컴퓨터는 이들을 모두 완전히 다른 이미지로 생각하게 된다는 겁니다. 오른쪽을 봅시다. 여러 물체 중 왼쪽 이미지에 해당하는 책이 있지만 크기와 각도가 다릅니다. 마찬가지로 픽셀 상으로 볼 때 아예 다른 이미지인 것이죠.

Image Patch

이를 위해 가장 먼저 우리가 해볼 일은 두 이미지의 유사도를 검출하는 것입니다. 이 때도 마찬가지로 우리는 Image patch 를 이용한 Filtering 을 활용할 것입니다. 두 영역을 비교하기 위해 Patch 값을 적용한 값을 벡터로 만들어 이 두 벡터를 비교합니다. 두 벡터가 비슷하다면 이미지의 두 구역은 유사하다고 판단할 수 잇는 것이지요.

그렇다면 어떠한 Image Patch 를 사용해야 의미있게 유사도를 구할 수 있는지가 관건일 겁니다. 가장 간단하게 생각해보면 그냥 무식하게 계산 없이 픽셀 값 그 자체로 하는 것입니다.

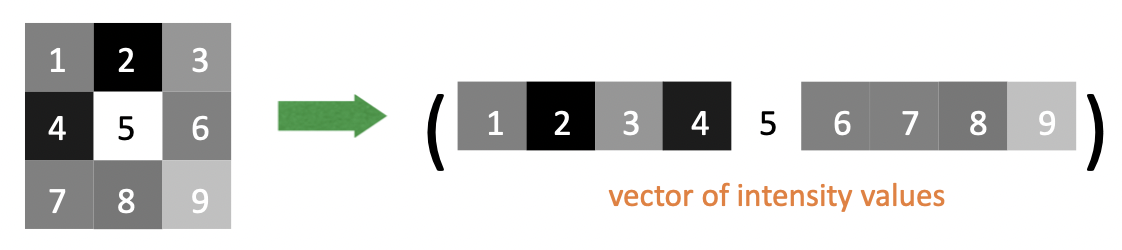
연산이 필요없이 간단하고 각 패치의 계산들이 독립적이기 때문에 병렬화가 잘 되서 정말 빠릅니다. 픽셀 값 자체를 하기 때문에 완전히 같은 이미지는 100%로 나오겠죠? 정말 Naive 한 방식이기 때문에 변형에 약할 수 밖에 없습니다. 간단히 생각해서 모든 픽셀 값들이 한 쪽으로 한 칸씩만 밀린다고 생각해봐도 완전히 큰 차이값(distance) 를 도출하게 될 것입니다. 하다 못해 조명이 달라져 전체적인 픽셀 값이 바뀐다 해도 모든 영역에서 실제 유사도가 낮아진다고 판단할 것입니다.

물론 Downsampling 과 같은 기법을 적용하면 픽셀의 주변 값들을 묶기 때문에 시프트와 같은 변형에 적응할 수 있습니다. 그렇다 하더라도 너무 많은 한계가 존재하기 때문에 널리 사용되기는 힘듭니다. 하지만 공장에서 불량 검사를 할 때처럼 외부적인 빛의 요인이 없이 오직 어디가 다른지만 판단하는 일에 아직도 사용되고는 한답니다.😄

그렇다면 우리 픽셀 값 자체대신 픽셀 값들의 변화량을 보는 건 어떨까요? 맞습니다. Image Gradients를 이용해보는 겁니다!

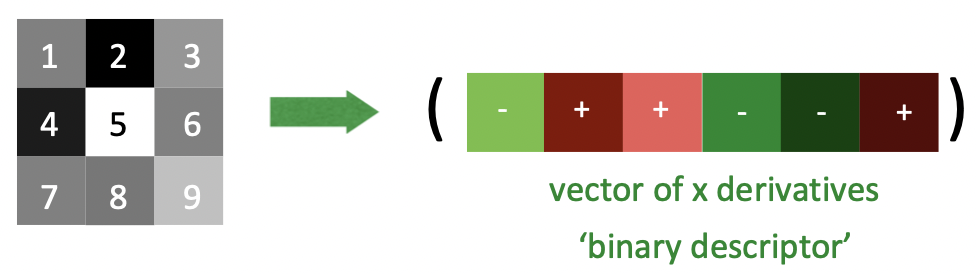
이렇게 되면 절대적인 픽셀 값에 대해서는 아예 영향을 받지 않을 겁니다. 어떤 부분이 밝아진다면 전체적으로 더 밝든 어둡든 결국 밝아지는 부분이라는 것은 비슷하다는 관점에서 제안된 아이디어입니다. 심지어 변화값(미분값)까지 타질 필요 없이 밝아지는, 어두워지는 부분이라면 동등하게 간주하기 위해 양인지 음인지만 이진법으로 표현합니다. 훨씬 효과적으로 보이는 방식이지만 마찬가지로 변형, deformation 에 약합니다.

예를 들어, 어떤 물체의 시점을 바꿔서 물체의 폭을 줄였다고 상상해 봅시다. 이를 같은 Image Patch 안에 넣는다면, 패치 안 같은 위치에 물체가 있는 부분과 없는 부분이 생기게 되겠지요...

Color Histogram

그래서 고안한 방식이 바로 Color Histogram 으로, Patch 내에 있는 RGB 색의 개수를 각각 세어서 Histogram 화 한 뒤 비교하는 것입니다.

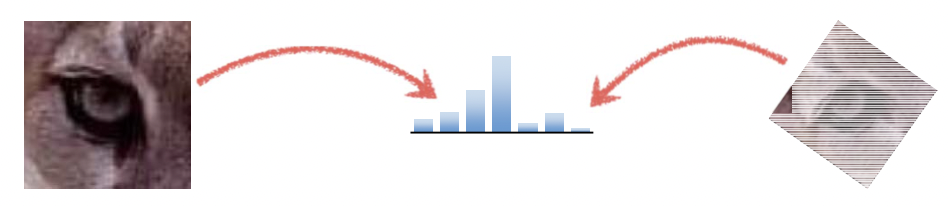
오른쪽 이미지는 왼쪽에 비해서 하얀색 선들이 그어져 있지만 이 흰색을 제외하고 나머지 색의 분포는 비슷한 겁니다. 또한 크기가 달라진다 하더라도 아니면 회전이 일어난다 하더라도 같은(비슷한) 이미지라면 해당 RGB 색상의 분포는 같을(비슷할) 것입니다. 이렇듯 장점이 많기 때문에 아직도 실무에서 쓰이는 방식입니다.

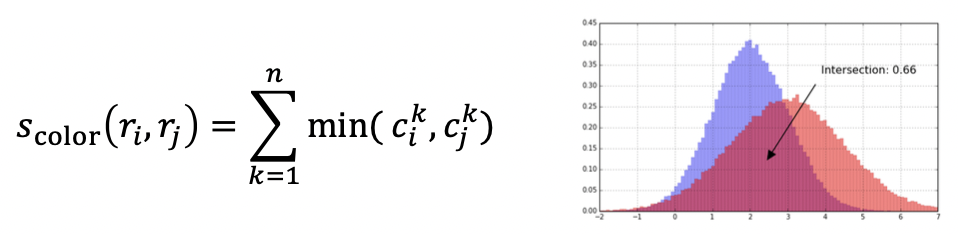
두 Histogram 의 유사도를 측정하기 위해서는 위와 같이 겹치는 영역을 계산하면 됩니다. 하지만 이러한 방식도 치명적인 문제가 있는데요. 아래의 그림을 봅시다.

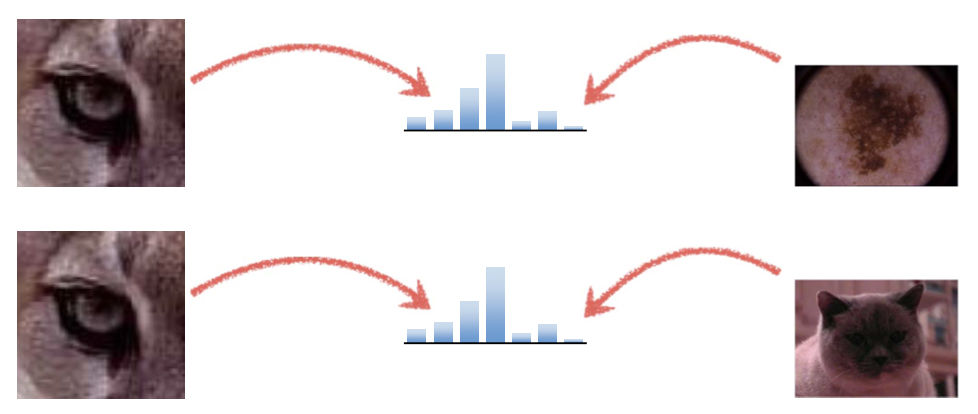
오른쪽 이미지들을 보면 분명 왼쪽 이미지와는 아예 다른 이미지, 아예 다른 오브젝트를 보이는 이미지입니다. 그런데 색만 본다면 상당히 유사하죠? 이것들을 Histogram 화 했을 때도 상당히 유사하다는 것입니다. 완전히 다른 이미지인데 말입니다. 즉, 색 분포의 공간적인 특성을 무시해서 이러한 결과가 발생하게 됩니다. 이를 보완하기 위해 나온 것이 바로 Spatial Color Histroram 입니다.

위와 같이 Image Patch 영역의 공간을 Cell 로 나눠서 해당 Cell 안에서 Histogram 을 뽑아 비교하는 것이지요. 그런데 만약 이미지가 회전 되었다면요? 완전히 다른 이미지 취급할 것입니다. Color Histogram 의 회전에 강한 장점이 사라져 버리는 것이지요.

이를 보완하기 위해 Orientation Normalization 을 수행해 줍니다. Image Gradient 값을 구해 가장 큰 값을 갖는 gradient의 방향을 기준으로 회전 각도를 보정해주는 것입니다. 이제 점점 더 복잡한(?) 방식들을 계속해서 알아보도록 하곘습니다.

GIST Descriptor

GIST Descriptor 는 2001 년에 Olivia와 Torrabla 과 고안한 Descriptor 입니다. 이는 하나의 필터링 결과만을 가지고 비교하기에는 이르니 여러 범위의 여러 필터들을 보고 비교를 하겠다는 간단한 아이디어에서 시작한 방식입니다. GIST 의 방식을 설명하면 아래와 같습니다.

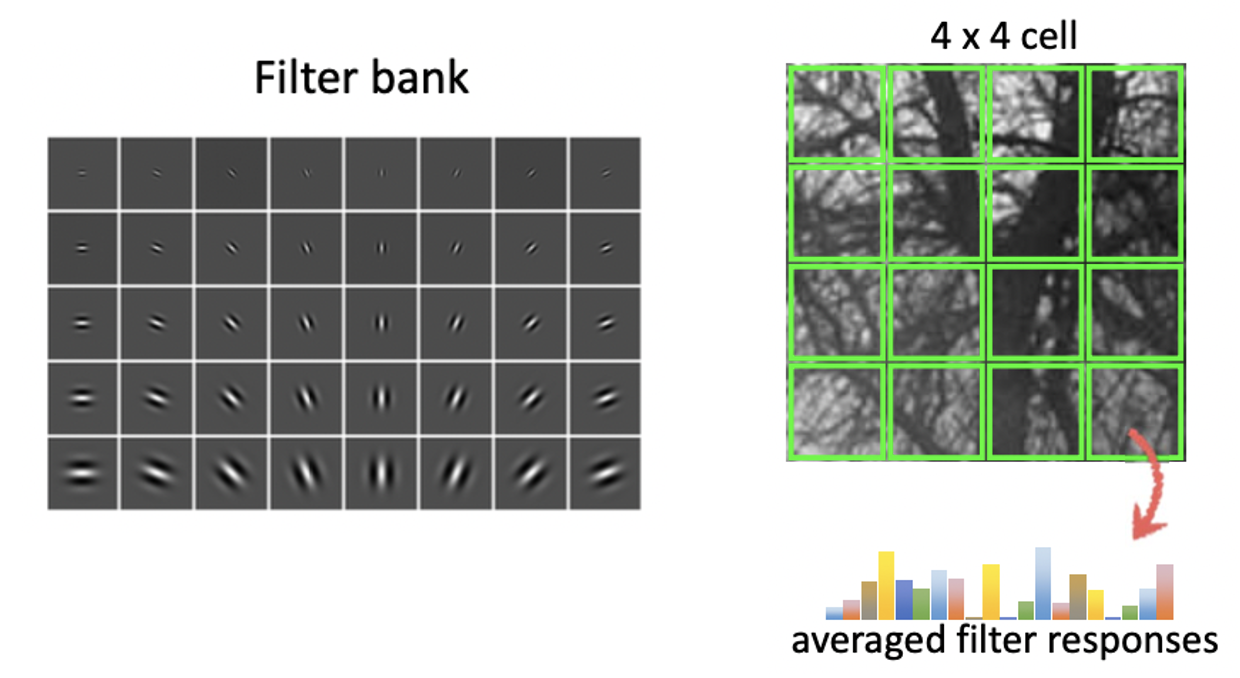
1. 왼쪽과 같이 parameter 를 바꿔가며 여러 Garbor Filter 들을 생성합니다. 위의 예시에는 Filter 의 개수 $N$ 이 40개이네요. 이것들을 Filter Bank 라고 표현합니다.
2. 이미지를 Spatical Color Histogram 을 했듯이 여러 Cell 들로 쪼개는 것입니다. GIST에서는 4 x 4 로 cell 을 쪼갭니다.
3. 이 16개의 cell 에 대해 각각의 cell 에 filter를 적용해 평균을 냅니다. 그러면 하나의 filter 에 대해 16개의 결과가 나오게 됩니다. 이 과정을 Filter Bank 의 $N$개에 대해 적용하면 총 $16N$의 값이 나오게 됩니다.

따라서 벡터의 dimensionality(차원)는 총 $16N$이 됩니다. 이 벡터를 비교함으로써 유사도를 측정하는 것이 바로 GIST Descriptor 입니다. 그러면 여기서 사용되는 filter 인 Garbor Filter 란 대체 무엇일까요?

Gabor Filter

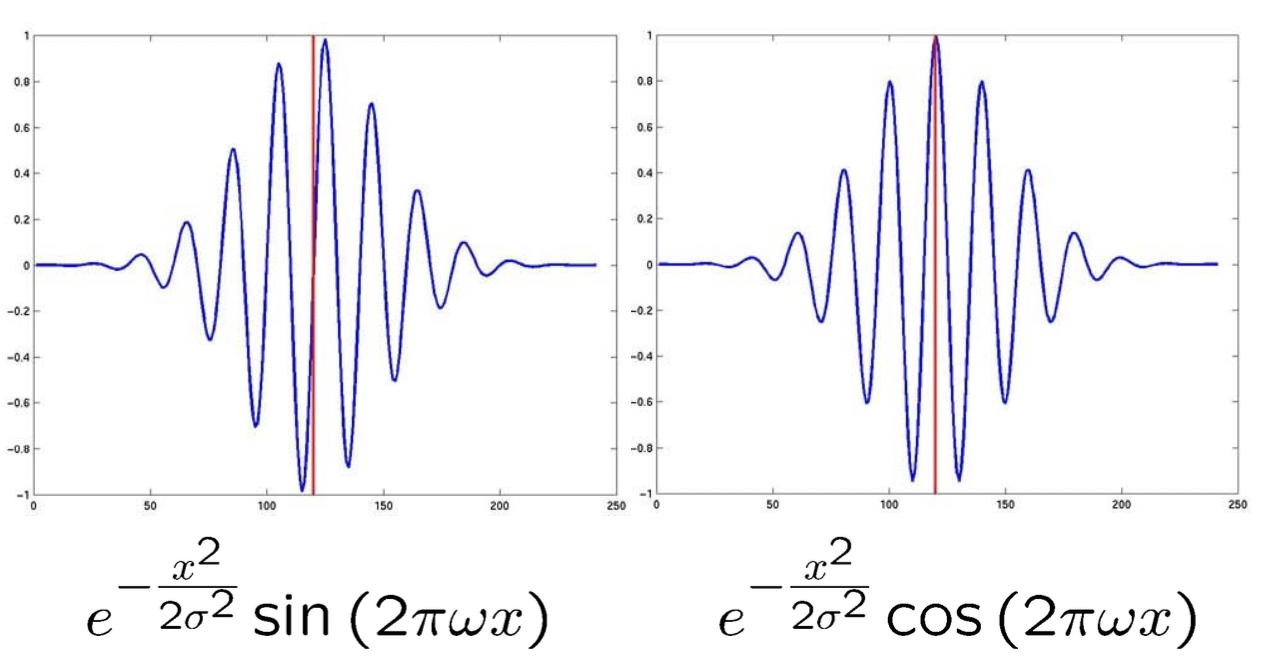
위와 같은 방정식을 봅시다. 보면 알겠듯이 파동을 표현하는 함수입니다. 여기서 $\sigma$ 값이 커질 수록 피크 값이 낮고 옆으로 퍼지는 형태가 됩니다. 또한 $w$ 값은 클수록 주기가 짧아지고 진동수가 작아져 촘촘한 형태가 되지요. 현재는 이 함수의 미지수가 $x$ 하나이기 때문에 1차원 방정식이지만 $y$ 까지 고려하여 2차원 형태를 취한 것이 바로 Gabor Filter 입니다.

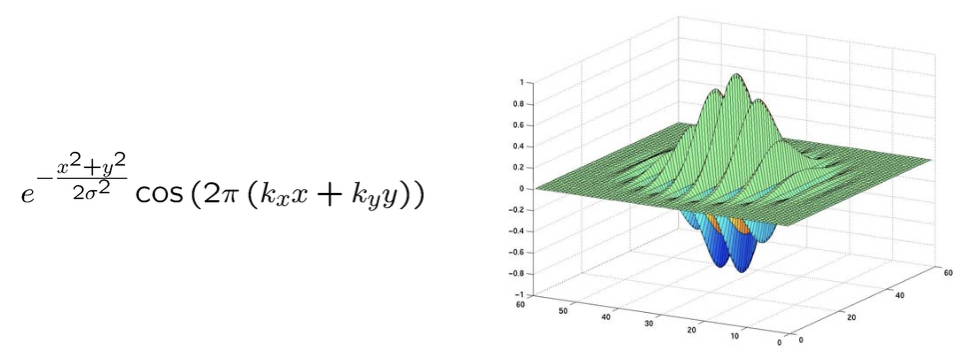
Gabor Filter 의 식과 3차원 그래프에서의 모양입니다. 이 식은 Even Gabor Filter 이며 Odd Gabor Filter 는 $cos$ 대신 $sin$ 을 적용한 필터입니다. parameter 로 $k_x$와 $k_y$ 값을 조정하여 이 필터의 회전 각도와 간격, 즉 진동수를 조절할 수 있습니다. 아래 그림은 결과값을 $z$ 축이 아닌 높은 하얗고 낮으면 시꺼면 색으로 표현하여 2차원으로 나타낸 모양입니다.

왼쪽에서 오른쪽으로 갈 수록 검정과 하양 사이의 간격(파동으로 표현하면 파장의 반)이 커지는 것을 볼 수 있습니다. $k_x$와 $k_y$ 의 절댓값이 점점 작아지는 것이지요. 가장 왼쪽의 그래프를 보면 필터가 $x$ 축에 평행한 모양을 하고 있습니다. $x$ 값에 대한 변화량이 없고, $y$ 값에 따라 정도가 변화합니다. $k_x$ 값이 0 인 것입니다. 이후 그림들을 보면 모양이 대각선 모양을 하고 있습니다. $k_x$ 값과 $k_y$ 값이 비슷한 것입니다. 이처럼 $k_x$ 와 $k_y$ 를 조절하여 간격과 각도를 조절할 수 있습니다.

이미지에 다양한 $k_x$와 $k_y$ 를 갖는 필터들을 적용한 response 결과입니다. 딱 봐도 뭔가 해당 필터처럼 생긴 영역이 필터링 되는 것이 보이지요?

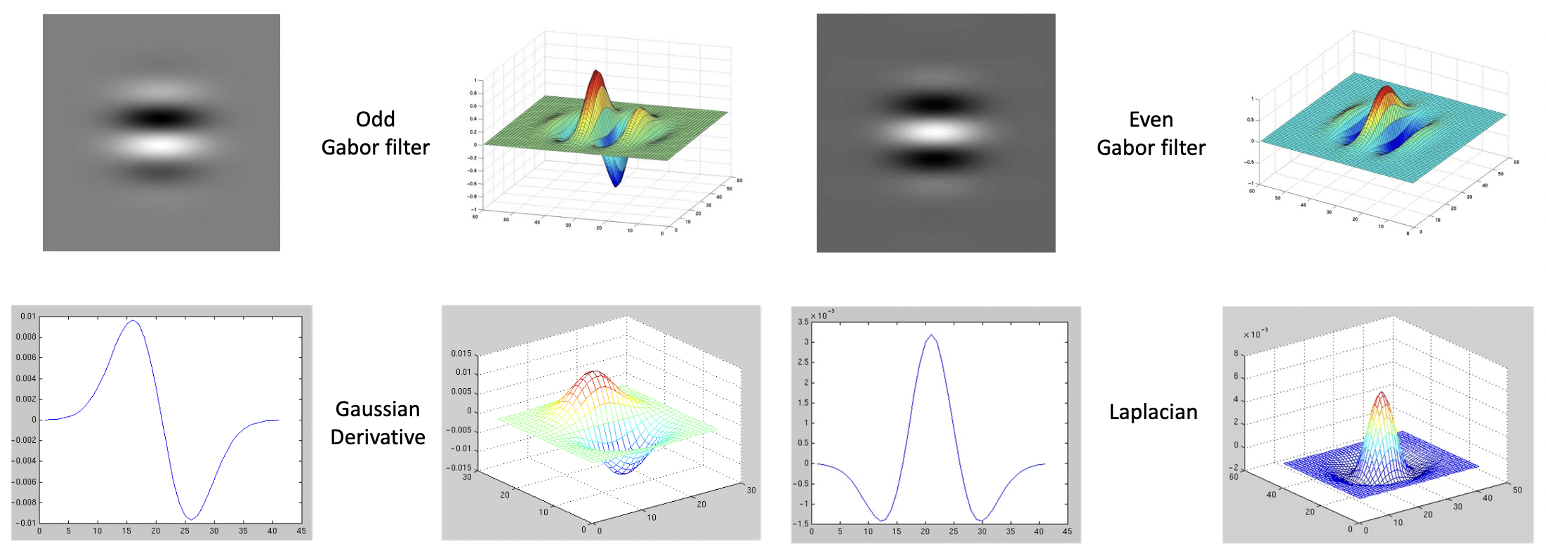
여기서 참 신기하게도 위와 같이 Odd Gabor Filter 그래프의 모습은 Gaussian 을 미분한 도함수인 Gaussian Derivative 의 그래프와 비슷합니다. 또한, Even Gabor Filter 는 Gaussian 을 두 번 미분한 이계도함수인 Laplacian 그래프와 비슷하지요.

이것이 Gabor Filter 입니다. 이 filter의 parameter 인 $\sigma$, $w$, $k_x$, $k_y$ 를 변화한 다양한 filter로 이루어진 Filter Bank 의 모습은 아래와 같습니다.

Gabor Filter 를 보면 값이 커졌다 작아지기 때문에 edge 에 걸맞는 것을 알 수 있습니다. Gabor Filter Bank 의 의의가 여러 방향으로 edge 를 찾는 것이기 때문에 다른 말로는 Directional Edge Detectors 라 부르기도 합니다.

HOG Descriptor

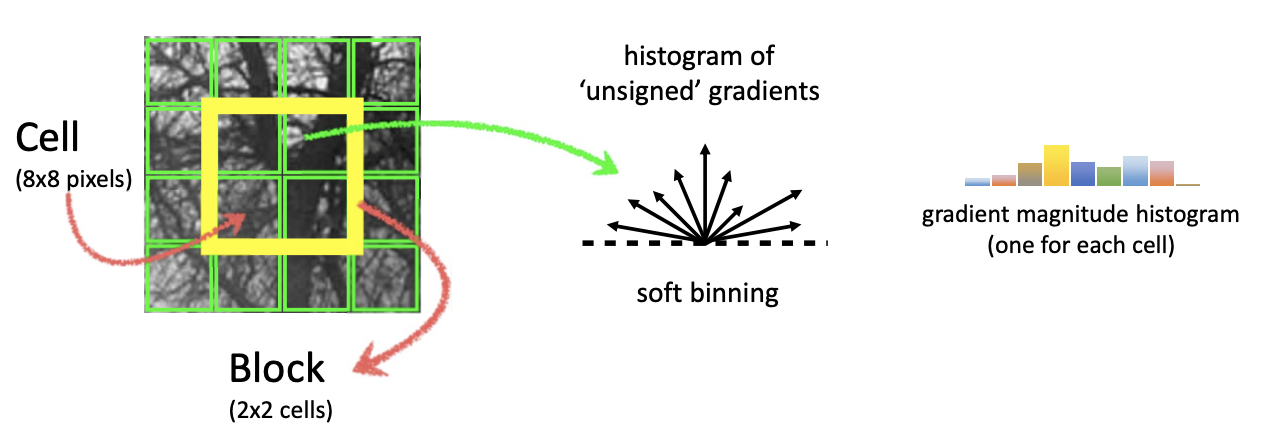
HOG Descriptor 는 2005년 Dalal와 Triggs가 고안한 방식입니다. HOG 는 gradient 의 histogram 을 그린다는 간단한 아이디어에서 개발되었습니다. GIST 와 마찬가지로 cell 을 나누고, gradient 를 구해서 direction(방향)별로 magnitude(크기)를 histogram 으로 구합니다. 예시는 아래와 같습니다.

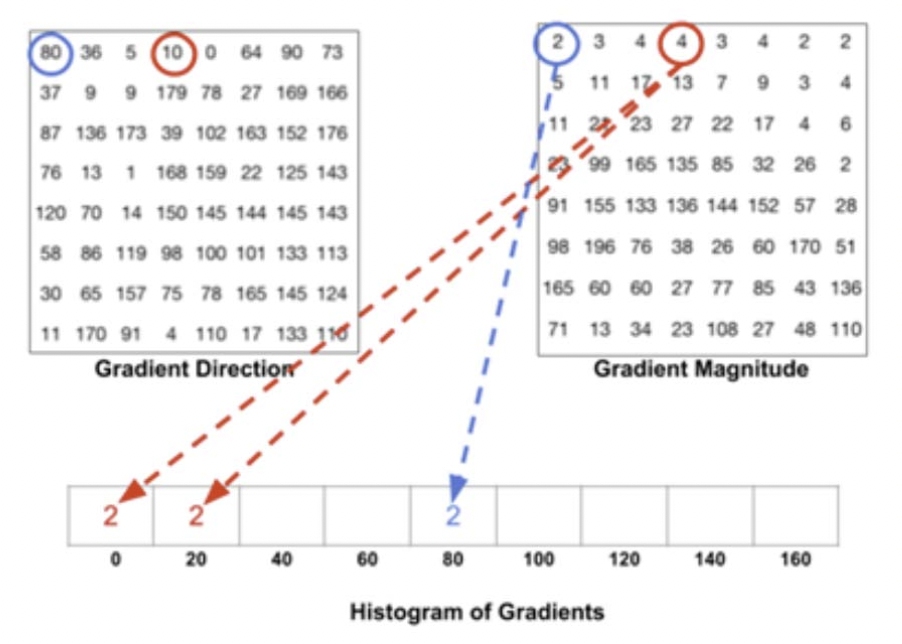
먼저 파란색을 보면 바향 80에 해당하는 픽셀에 대해서 크기가 2이기 때문에 histogram 의 80에 2를 더합니다. 빨강을 보면 방향 10에 해당하는 픽셀의 크기가 4입니다. 10은 histogram 상에서 0과 20의 딱 중간이기 때문에 크기 4를 반으로 나누어 각각에 2씩을 더해줍니다.

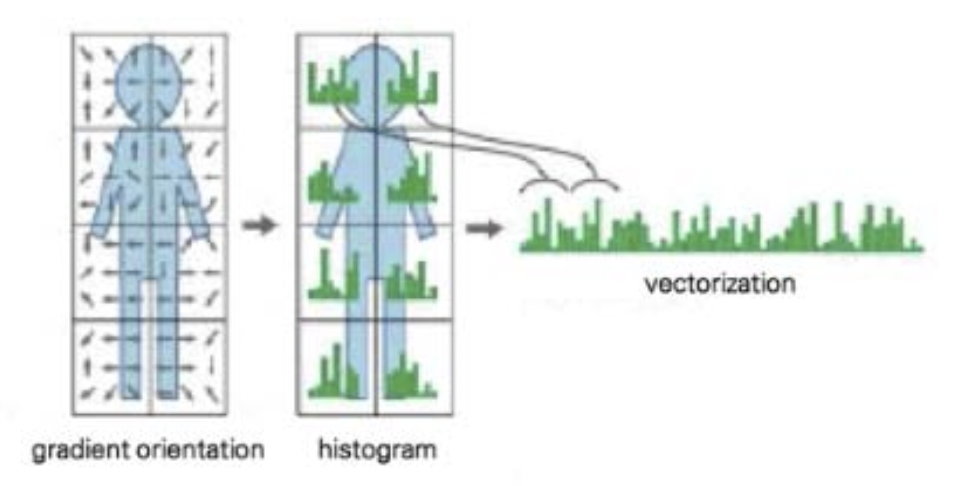
그리고 각각에 cell 에 대해 구한 histogram 값을 하나의 벡터로 합쳐 이를 비교함으로써 유사도를 구하는 것이 바로 HOG Descriptor 입니다.

다음 글에 이어서 마지막 Descriptor를 알아보도록 하겠습니다.