요즘 들어, 제가 관심이 생긴 분야가 바로 Computer Vision입니다. 우리의 오감인 시각, 청각, 후각, 미각, 촉각 중 무엇이 가장 중요하다고 생각하시나요? 말을 바꿔서, 다섯 가지 중 하나만 택해야 한다면 무엇을 선택하시겠나요? 저는 시각을 선택할 거 같습니다. 시각이 없었을 때의 불편함이 압도적으로 클 것 같거든요. 실제로 감각 기관별 정보 수용량을 보면 시각이 무려 83%를 차지한다고 합니다. 컴퓨터의 눈이 되어주는 컴퓨터 비전 분야에 대해서 공부해보는 시간을 가지겠습니다.

Types of Image Transformation

우리는 실생활에서 무수히 많은 이미지들을 마주합니다. 디지털, 즉 컴퓨터에서 표현되는 이미지는 하나의 커다란 2차원 배열입니다. Pixel(픽셀)이라는 색상 정보를 표현하고 있는 요소들로 이루어져 있지요. 위의 그림과 같이 우리 눈에는 자연스럽게 이어지는 이미지도 확대해보면 픽셀이라는 격자 무늬로 이루어져 있음을 볼 수 있습니다. Resolution(해상도)라는 말은 많이 들어보시죠? 대표적으로 1920x1080이 있는데, 이는 간단히 가로 1920개, 세로 1080개의 픽셀로 이루어져 있음을 의미하며 FUll HD(FHD)라고 합니다. 조금 더 알아보자면 3840x2160을 우리가 4K라고 하는데, FHD이미지를 4K 모니터에 띄우면 이미지 픽셀 하나가 모니터 픽셀 4(2x2)개에 매핑되어 투박하게 깍두기 모양으로 보이게 되는 것입니다.

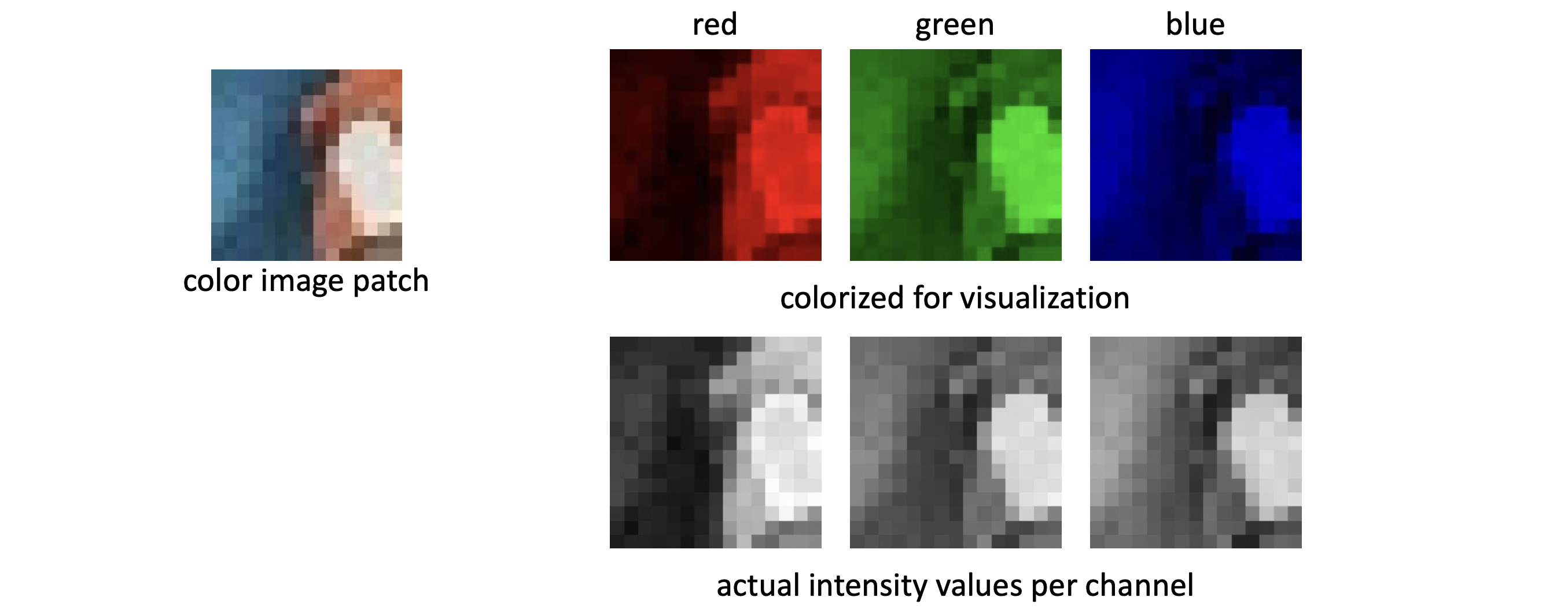
그런데 사실 픽셀 하나는 색상을 표현하기 위해 Red, Green, Blue의 RGB로 이루어져 있습니다. 그래서 결론적으로 이미지는 (가로 픽셀) x (세로 픽셀) x 3(RGB)의 3D Tensor입니다. 1차원은 Vector(벡터), 2차원은 Matrix(매트릭스)임을 아실겁니다. Tensor(텐서)는 이를 일반화한 것으로 다차원의 배열을 의미합니다. 따라서, 3D Tensor는 3차원의 텐서를 의미하는 것이지요. 위와 같이 각각의 RGB들의 조합으로 하나의 컬러 이미지가 나타나는 것입니다. 실제로는 RGB가 위의 세 그림같이 색칠되어 있지 않고, 각각의 색상들이 scalar 값으로 아래와 같이 나타납니다. 검정색이 진할수록 해당 색상 성분의 값이 낮고, 밝을 수록 성분의 값이 높음을 의미합니다. 이 Intensity는 가장 일반적으로 0~255까지 1바이트로 강도를 discrete하게 나타냅니다.

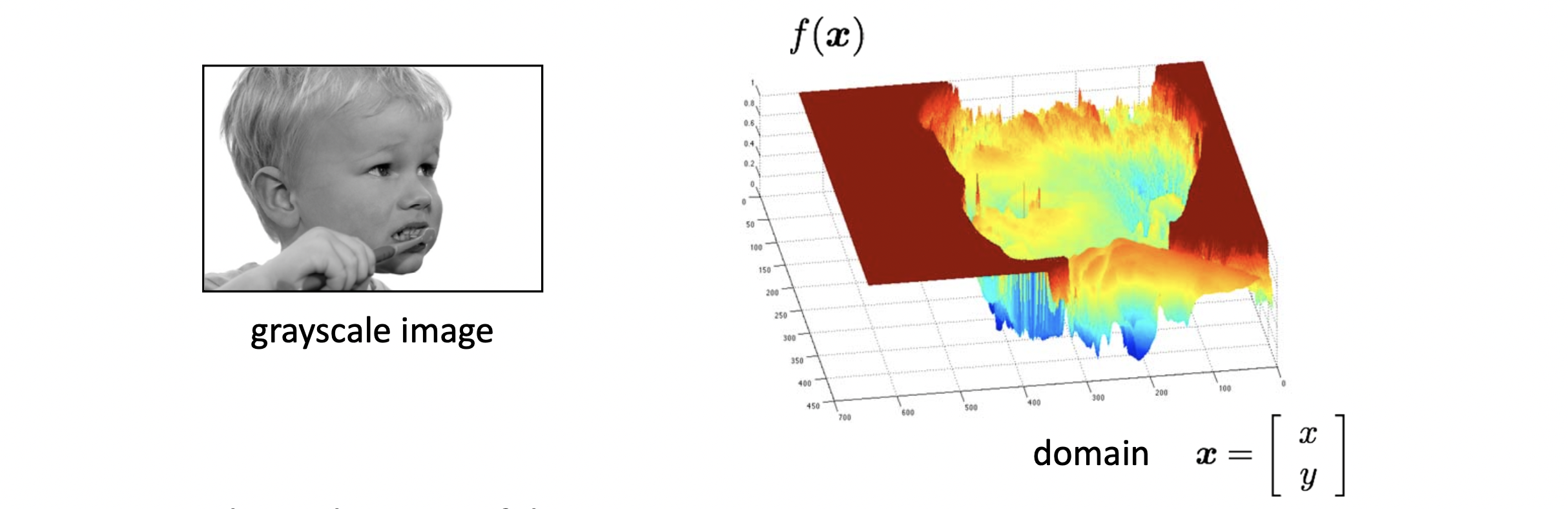
하지만, 앞으로는 설명의 편의를 위해 RGB를 고려하지 않은 Grayscale(흑백) 이미지를 주로 이야기 하겠습니다. 흑백 이미지는 색상과는 관계없이 해당 픽셀에 얼마나 많은 빛이 들어오고 있는지만 고려합니다. 밝은 부분은 빛이 만들어와서 Intensity가 높은 밝은 영역이고, 어두운 영역은 빛이 적어 intensity가 낮은 어두운 영역이 됩니다. 위의 사진에서 왼쪽의 그림의 가로를 $x$축, 세로를 $y$축, 빛의 세기를 z축으로 하면 $f(x,y) = (Intensity)$의 2D 함수로 나타낼 수 있습니다. 오른쪽의 그림은 이를 그래프로 표현한 것입니다. 이렇게 함수를 통해 우리가 미분과 같은 게산들을 거친다면 이미지로부터 유의미한 정보를 얻을 수 있게 되겠지요?

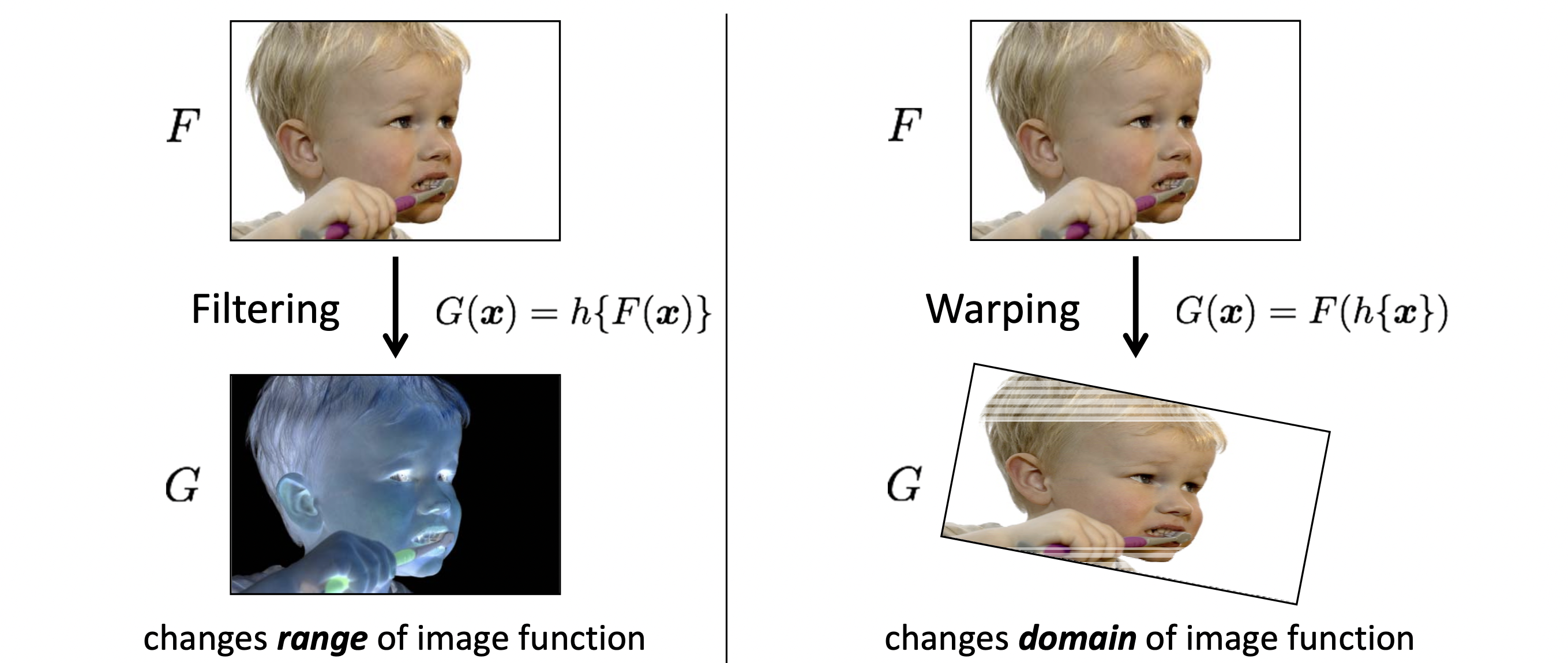
우리가 공부할 Image Transformation(이미지 변형)의 경우에는 위와 같이 크게 Filtering과 Warping 두 종류로 나뉩니다. 먼저 Filtering은 이미지의 픽셀들에 대하여 각 픽셀들의 값을 변화시키는 것을 의미합니다. 이미지의 차원, 크기 모양 등은 그대로이지만 픽셀의 값, 즉 앞에서 얘기했던 Intensity 값을 변경하는 것입니다. 이미지의 Range를 바꾼다고도 표현합니다. Warping은 반대로 이미지의 픽셀 값은 건드리지 않고, 이미지의 각 픽셀들의 위치를 변화시키는 것을 의미합니다. 위 그림과 같이 이미지를 돌리고 가로로 늘리고 하는 변형들을 의미합니다. 이미지의 domain을 바꾼다고도 표현합니다.

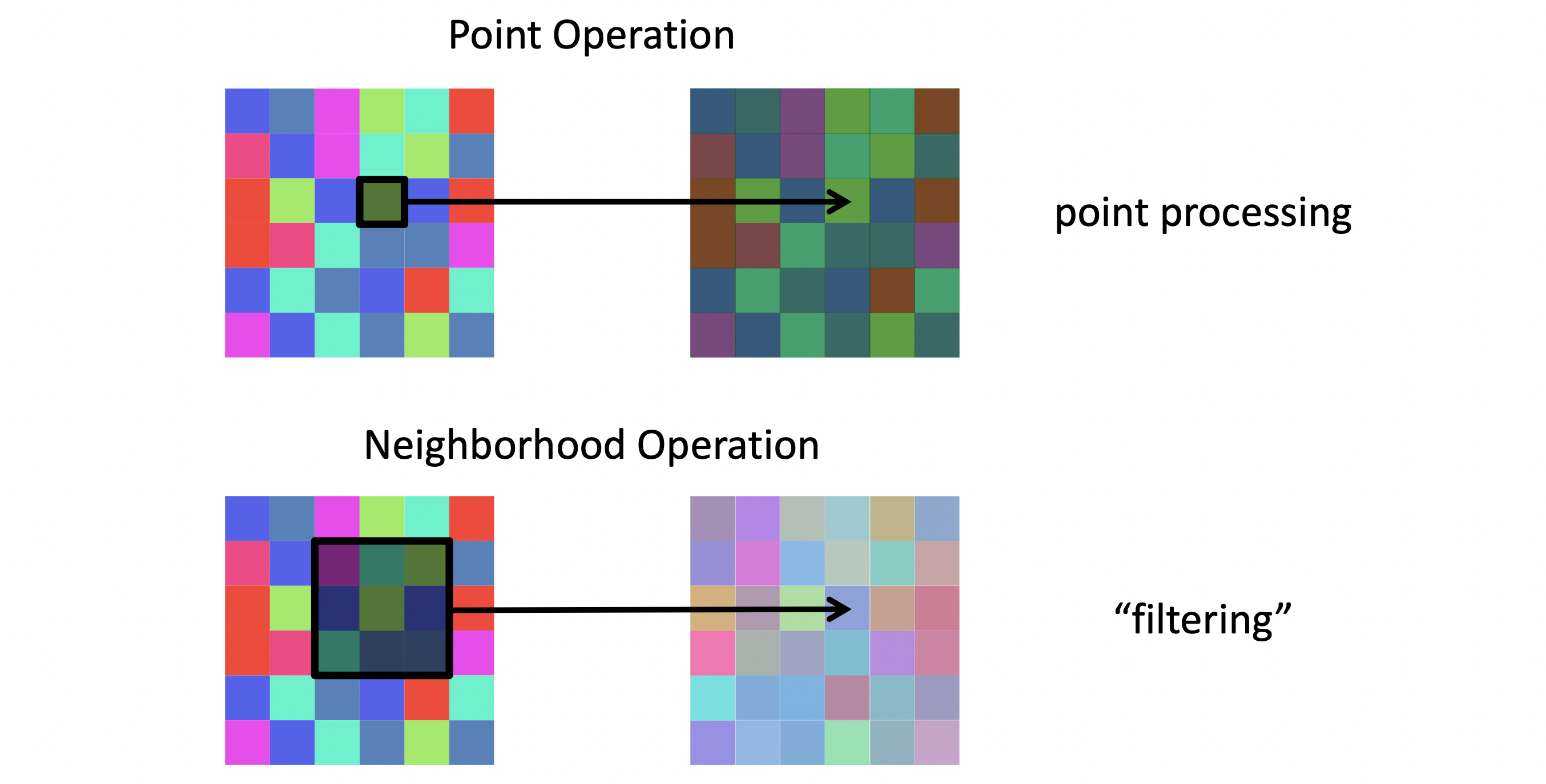
Image Filtering도 크게 두 가지로 나눠볼 수 있겠는데요. output 이미지의 픽셀이 input 이미지의 해당되는 한 픽셀에서만 영향을 받으면 이를 Point Operation이라고 합니다. 1대 1 매핑을 하는 방식, 즉 point-to-point이지요. 그리고 output 이미지의 픽셀이 input 이미지의 해당되는 픽셀 뿐 아니라 주변 픽셀 값까지 고려하여 영향을 받으면 이를 Neighborhood Operation이라고 합니다.

위와 같이 한 픽셀 값을 조정하여 이미지에 다양한 효과를 불러 일으킬 수 있습니다.

Linear Shift-Invariant Image Filtering

Filtering 중 Linear Shift-Invariant Image Filtering은 하나의 픽셀을 주변 픽셀들과의 Linear Combination으로 대체하는 필터링을 의미합니다. 이게 무슨 말이냐 하면 먼저 필터의 Kernel(커널)을 만듭니다. 이 커널은 각 해당 픽셀에 대한 Weight(가중치) 들의 행렬입니다. Box Filter, 2D rect filter, square mean filter 등 다양한 이름으로 불리죠.
input 픽셀에 이 커널을 대입하여 각 가중치와 픽셀 값을 곱한 값들을 더합니다. 이 과정을 Combination이라고 하며, 이 값을 최종적으로 output 픽셀 값을 매핑하는 겁니다. 그리고 이 커널이 input 이미지의 처음부터 끝까지 이동하면서 output 픽셀 값들을 모두 계산하면 비로소 output 이미지가 만들어지는 것이지요. 이해가 힘드니 그림으로 설명하면서 가볼까요?

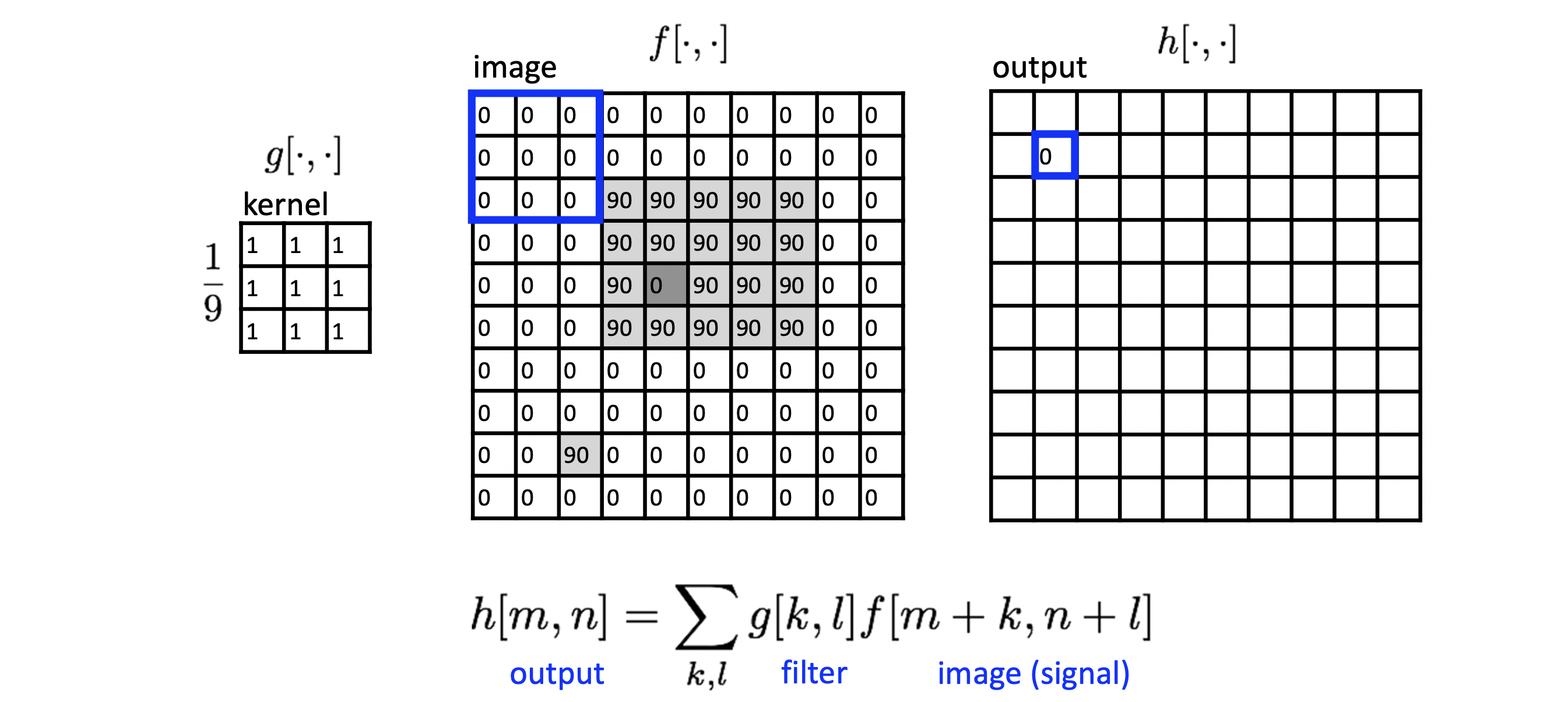
왼쪽에 커널이 있습니다. $3 \times 3$ 커널이며 가중치는 모두 $\frac{1}{9}$이네요. 이미지의 처음부터 커널을 대입해보면 결과 값은 $0 \times \frac{1}{9} + 0 \times \frac{1}{9} + ... = 0$이 되어 해당 output 픽셀의 값이 0이 됩니다. 이 커널은 오른쪽으로 이동하면서 끝에 도달할 시 한 칸 내려와 똑같은 과정을 계속해서 반복합니다. 마치 걸레로 창문을 닦는 것 같습니다.😆

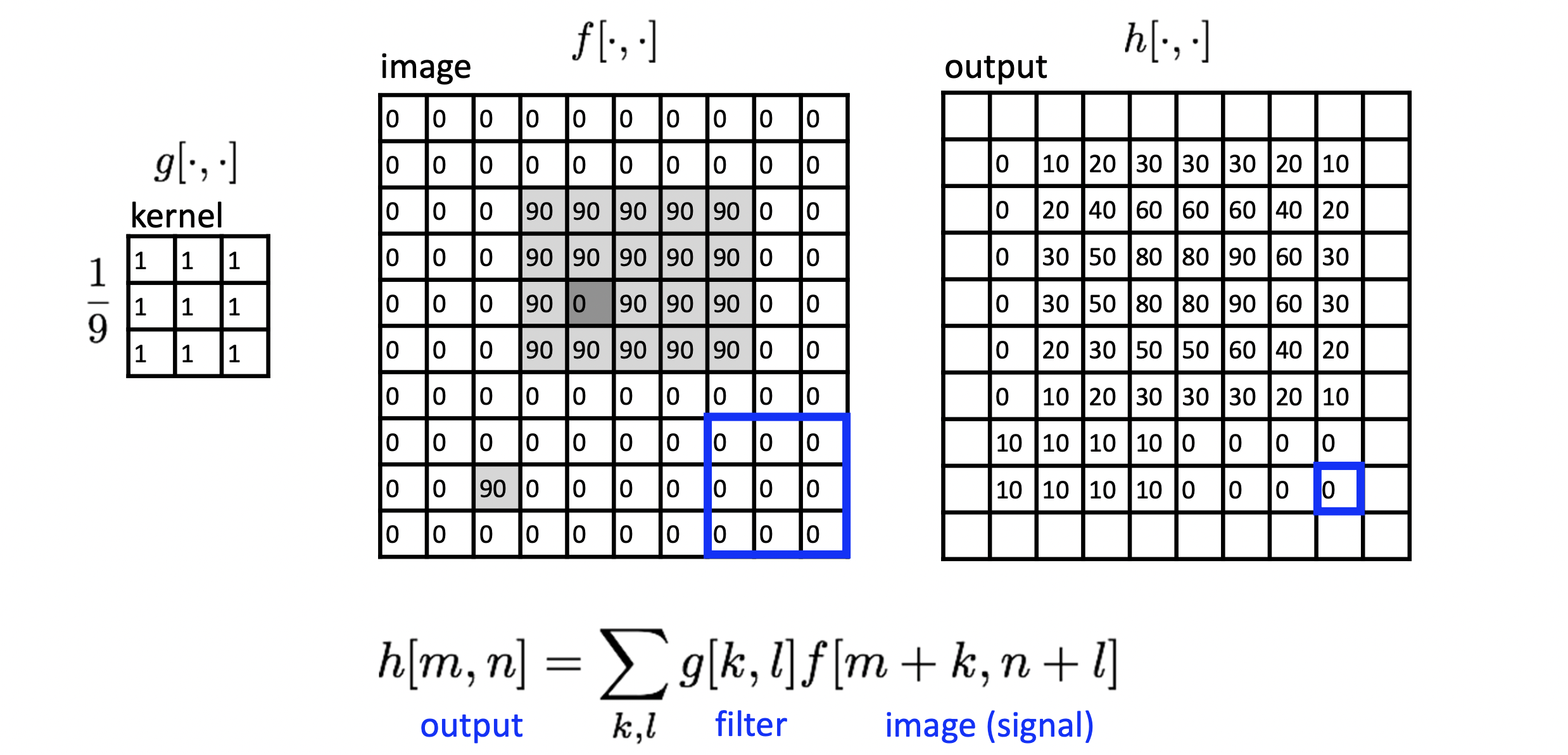
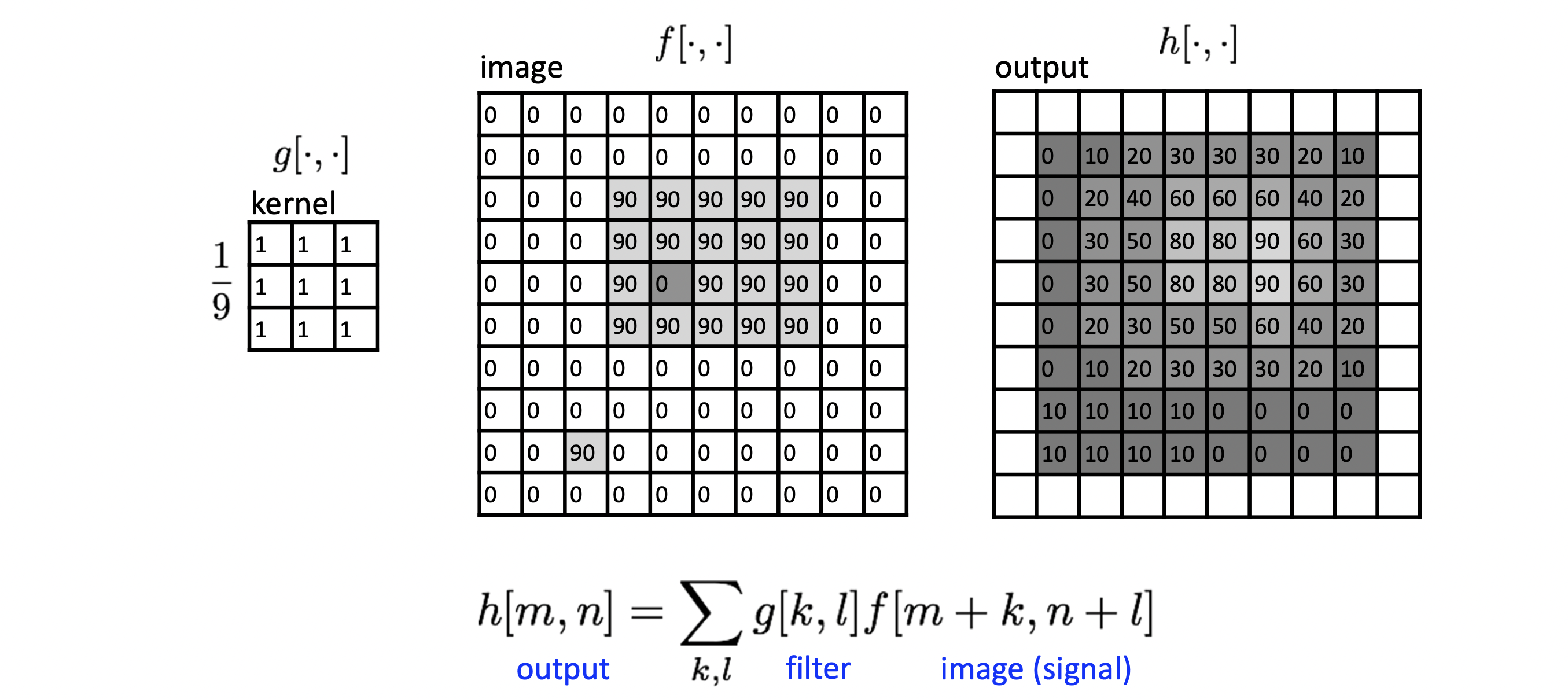
끝에 도달한 모습은 위와 같습니다. output 이미지의 픽셀 값들을 input 이미지의 픽셀 값들과 비교해보면 값이 작아지며 전체적으로 퍼져있는 양상을 볼 수 있죠? 실제로 결과물을 확인해보면 이미지들이 블러 처리 효과가 적용되어 있음을 확인할 수 있습니다. 주변과 비슷하게 동화되는 평균의 효과 때문이죠!

Linear Shift-Invariant 필터는 이름이 설명하듯 Linearity와 Shift Invariance를 가집니다. Linearity는 $f_1$과 $f_2$를 각각 하나의 행렬이라 했을 때 $filter(f_1 + f_2) = filter(f_1) + filter(f_2)$를 만족한다는 뜻입니다. 각각에 필터를 적용해 더한 값과 둘을 미리 더하고 필터를 적용한 값이 같다는 것이죠. Shift Invariance는 필터링에 있어서 픽셀의 위치는 전혀 관련이 없다는 점입니다. 즉, 같은 값이라면 어느 위치에서도 해도 동일한 값이 나와야 한다는 것이죠.

Separable Filter

그 다음으로 확인할 것은 바로 Separable Filter입니다.

어떤 필터가 위와 같이 column 벡터와 row 벡터의 곱으로 표현이 됬을 때 우리는 그 필터를 separable하다라고 표현합니다. 그러면 어떤 필터가 separable 하기 위해서 이 필터 행렬의 Rank(랭크)는 어떻게 되야할까요? 랭크가 뭐냐고요? 위의 박스 필터를 보면 $3 \times 3$ 행렬이기에 하나씩 세 개의 벡터로 구성되어 있습니다. 이 세 백터 중 Linearly Independent한 벡터의 개수를 랭크라고 합니다.세 벡터를 $v_1, v_2, v_3$라고 할 때 만약 $v_1 = 2 \times v_2 + 4 \times v_3$ 처럼 남은 벡터의 조합으로 표현할 수 있다면 이것은 linearly dependent 한 것이 됩니다. 다시 돌아와서, separable한 matrix를 위해 필요한 랭크는 1입니다.

필터가 separable할 이유는 뭘까요? 우리가 만약 $M \times M$ 픽셀을 가지는 이미지에 $N \times N$ 커널을 적용한다면 하나의 이미지를 필터링 하는 데 걸리는 시간, 즉 연산의 수는 얼마나 될까요? 한 번 커널을 적용하는데 $N^2$이 걸립니다. 모든 픽셀의 수는 $M^2$개니 총 $N^2M^2$의 비용이 소모됩니다. 그런데 만약에 필터가 separable 하다면 이 비용을 $2NM^2$로 줄일 수 있습니다. 왜냐면 커널을 적용하는 데 matrix가 아니라 column 벡터를 적용한 후 그 값에 row 벡터를 적용하면 되기 때문에 $N + N = 2N$이 소모되기 때문이죠.

The Gaussian Filter

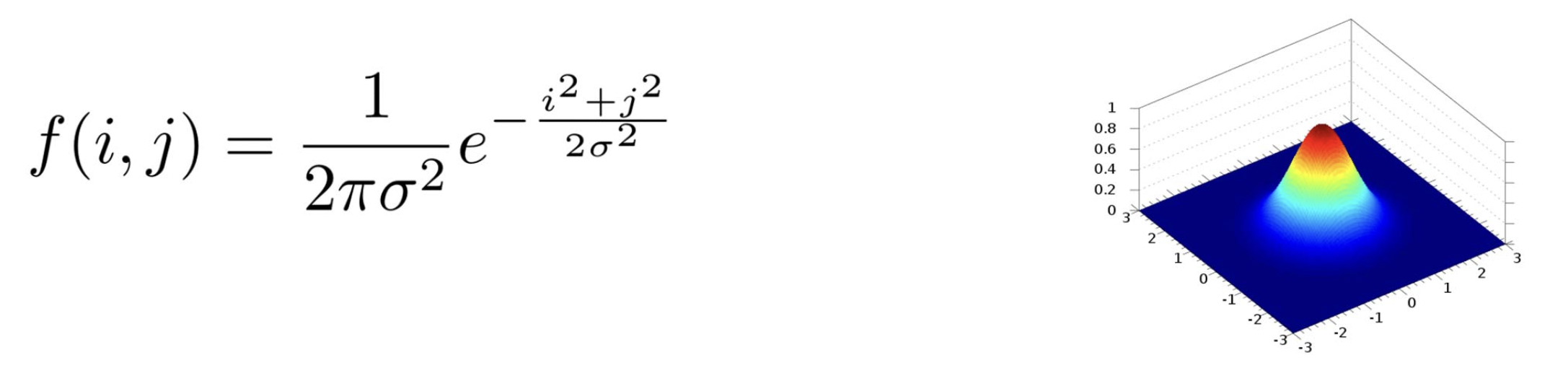
확률과 통계 같은 과목을 공부하면서 Gaussian(가우시안) 함수는 꼭 한 번 들어봤을 겁니다. 수식은 복잡하지만 가우시안의 가장 큰 특징은 다음과 같습니다.

원점에서 멀어질수록 값이 작아진다.

이 점을 필터에 적용해서 주변과 linear combination을 하되 center 픽셀, 즉 원본 위치의 기존 픽셀 값을 가장 크게 반영하겠다는 뜻이 되는 것이죠. 이론적으로, 가우시안 함수는 아무리 무한대로 멀어지도 값이 0 이상입니다. 그러나 우리가 실제로 쓰는 필터는 크기에 한계가 있기 때문에 아래와 같은 형태가 됩니다.

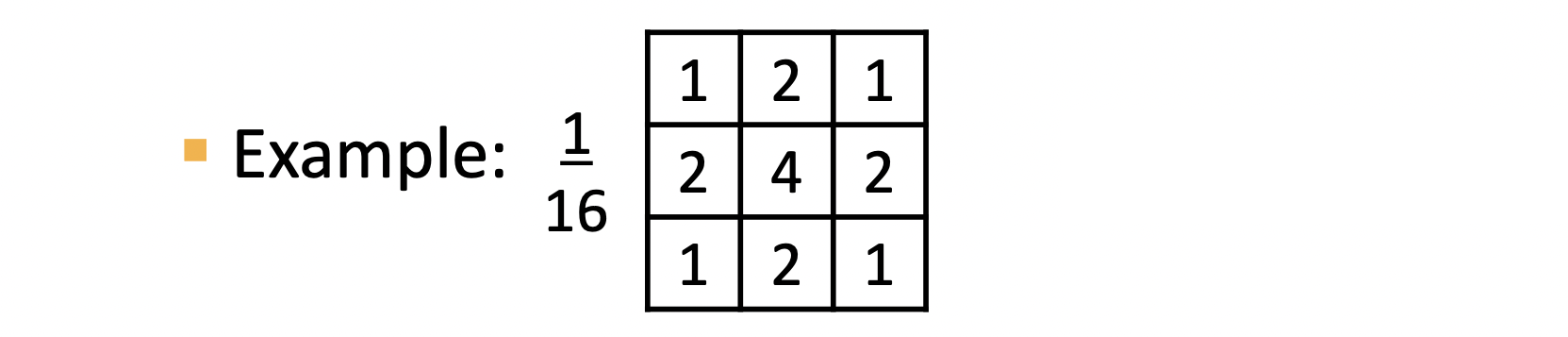
필터 앞에 다음과 같이 필터 앞에 $\frac{1}{16}$은 존재하는 것은 Normalization을 하기 위함입니다. 필터 안의 값들이 모두 1이 넘는데 필터를 적용한 값은 픽셀 하나 에 적용되는 값이기 때문에 너무 커서 조정을 하는 것이죠. 아래는 기존의 Box Filtering과 Gaussian을 비교한 예시입니다.

똑같이 평균을 취해 blur 처리를 해주지만, Gaussian은 원래 픽셀과 가까울 수록 값을 크게 반영해 조금 더 원본을 살리는 효과가 있음을 확인할 수 있습니다. 이렇게 효과적인 blur 처리를 위한 가우시안을 원본 이미지와 겹치면 아래 그림과 같이 그림자 처리를 할 수 있습니다.

커널, 즉 필터의 사이즈가 커지면 커질 수록 blur 처리되는 면적 또한 커지기 때문에 위와 같이 다른 효과들이 나타나게 되는 것이 특징입니다.

Other Filters

다른 필터들을 계속해서 알아보도록 합시다.

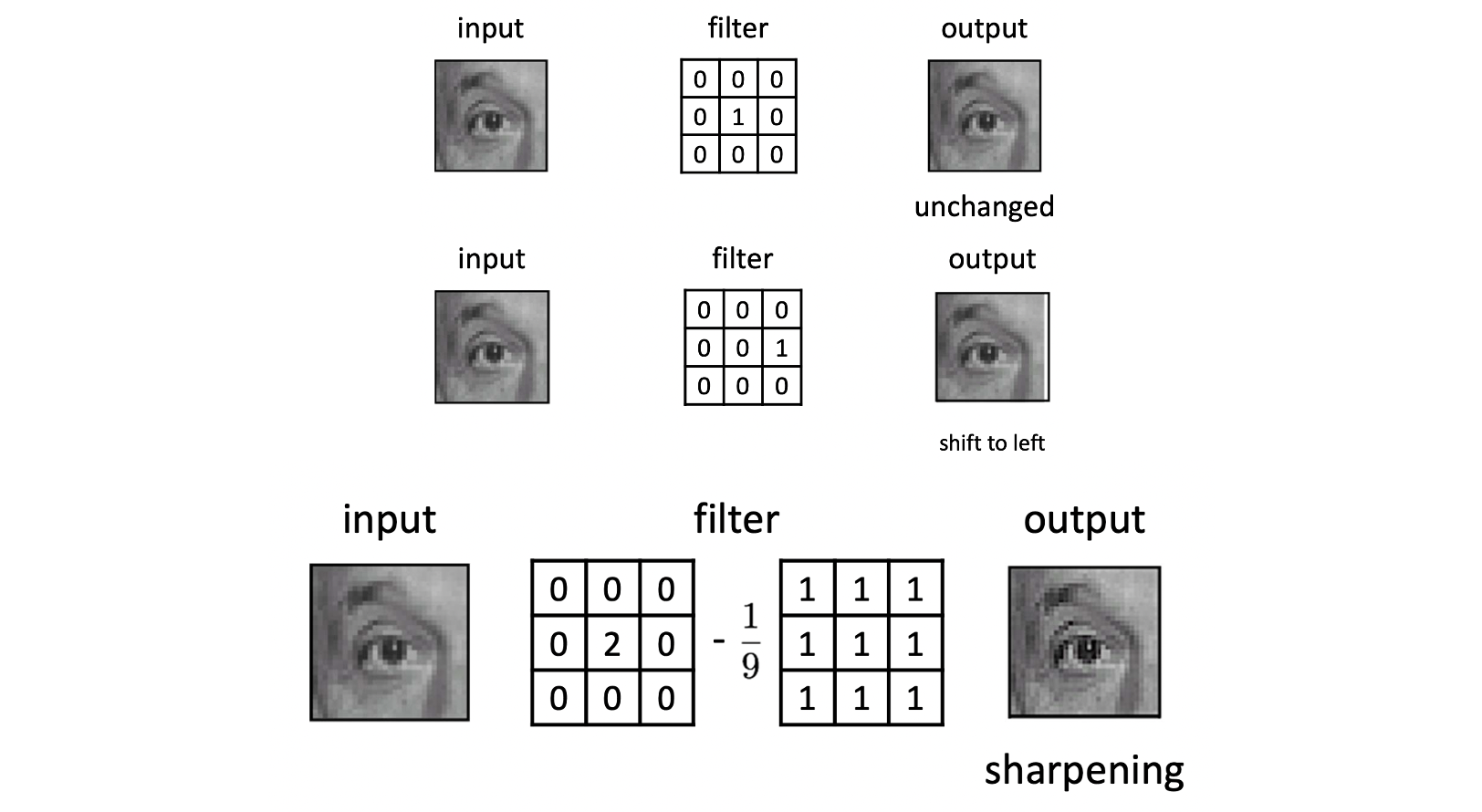
첫 번째는 딱 봐도 알겠지만 원본을 유지하는 필터가 됩니다. 두 번째를 보면 어떤 픽셀에는 그것의 오른쪽의 픽셀 값을 적용하는 것을 알 수 있습니다. 결과적으로 픽셀 값들이 왼쪽으로 이동해 이미지 자체가 왼쪽으로 한 픽셀만큼 이동하는 것이지요. 세 번째를 볼까요? 특이하게도 원본 픽셀 값을 2배 증가시킨 다음에 주변의 값들은 오히려 약간씩 빼 줍니다. 이는 내 픽셀 값은 강화하고, 주변은 약화시키는 결과를 초래합니다. 결과적으로 나와 내 주변의 차이가 더 극명하게 드러나서 선명하게 해줍니다. 이를 Sharpening이라 합니다.

원본 값에 주변과 평균을 낸 blur 처리된 값을 빼면 어떤 픽셀과 주변의 차이를 나타내는 detail 이미지가 결과로 나오게 됩니다. 이 이미지를 다시 원본 이미지에 더하면 기존 이미지에서 주변과 차이가 나는 부분이 강조된 선명한(sharpened)이미지를 얻을 수 있는 것이지요. 이를 적용한 예시는 아래와 같습니다.

Dealing with Boundaries

필터링을 하면서 빠질 수 없는 이슈가 바로 경계값 처리입니다. 위에서 필터링을 위해 보여드린 이미지를 다시 가져와 보겠습니다

필터를 적용하면 이미지의 테두리 값들은 필터링을 할 수 없기 때문에 날아가서 이미즈이 크기가 작아지는 문제가 생겨 버립니다...그래서 필터링을 하고 난 뒤의 이미지의 크기가 원본과 같도록 임시로 원본 이미지를 키우는, 즉 뻥뛰기 하는데 이를 Extrapolation(외삽)이라고 합니다. 외삽에는 다음 이외에도 여러 테크닉이 존재합니다.

• Black : 소스 이미지의 바깥 모든 픽셀을 검정색으로 붙이는 겁니다. 다만, 이렇게 되면 결과적으로 검정이 안으로 침범하게 되서 테두리가 거뭇거뭇 해질 수 있는 문제가 있습니다.
• Cyclic Wrap : 반대 쪽의 이미지를 덧붙이는 방식입니다. 예시로, 위쪽에는 아래쪽 테두리의 픽셀이들이 붙는 것이지요. 마치 원통으로 돌돌 말은 형태와 같다 해서 이렇게 명명 되었습니다. 다만, 양쪽 사이드의 색깔이 많이 다르게 되면 이것 또한 침범 문제를 피할 수 없습니다.
• Copy Boundary : 그냥 해당 테두리 픽셀들을 복사해서 덧붙이는 방식입니다. 노이즈가 클 수 있다는 문제를 안고 있습니다.
• Reflect acros boundary : copy boundary 방식과 동일하지만 마치 데칼코마니처럼 이를 반사시켜서 덧붙이는 방식입니다.

Median Filtering

Median Filtering은 말 그대로 필터 영역의 픽셀 값들 중 중간값을 취한다는 의미입니다.

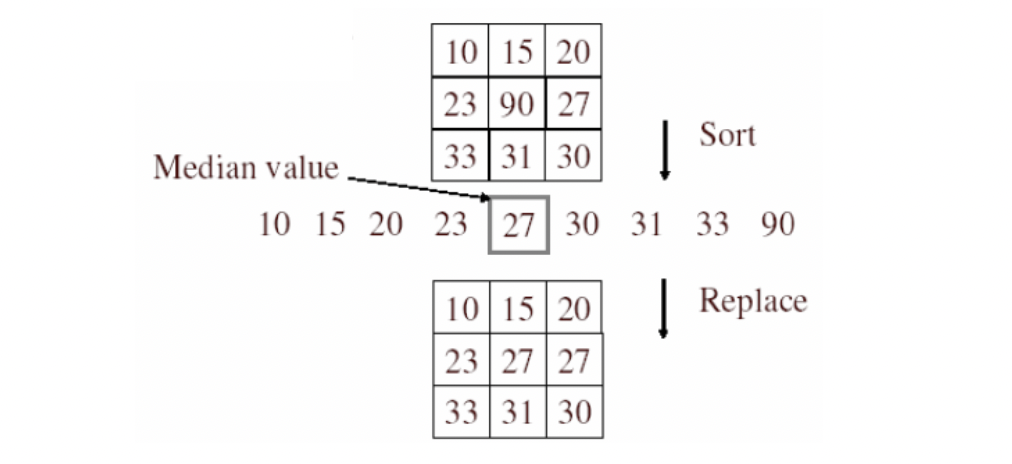
Median Filtering에 가장 큰 특징은 Outlier에 강하다는 것입니다. Outlier는 주변에 비해 유난히 _튀는) 픽셀 값을 의미합니다. 기존처럼 평균을 적용해버리면 쓸데 없이 이 튀는 값에 영향을 많이 받는데, 중간값으로 구해버리면 이를 무시할 수 있습니다.

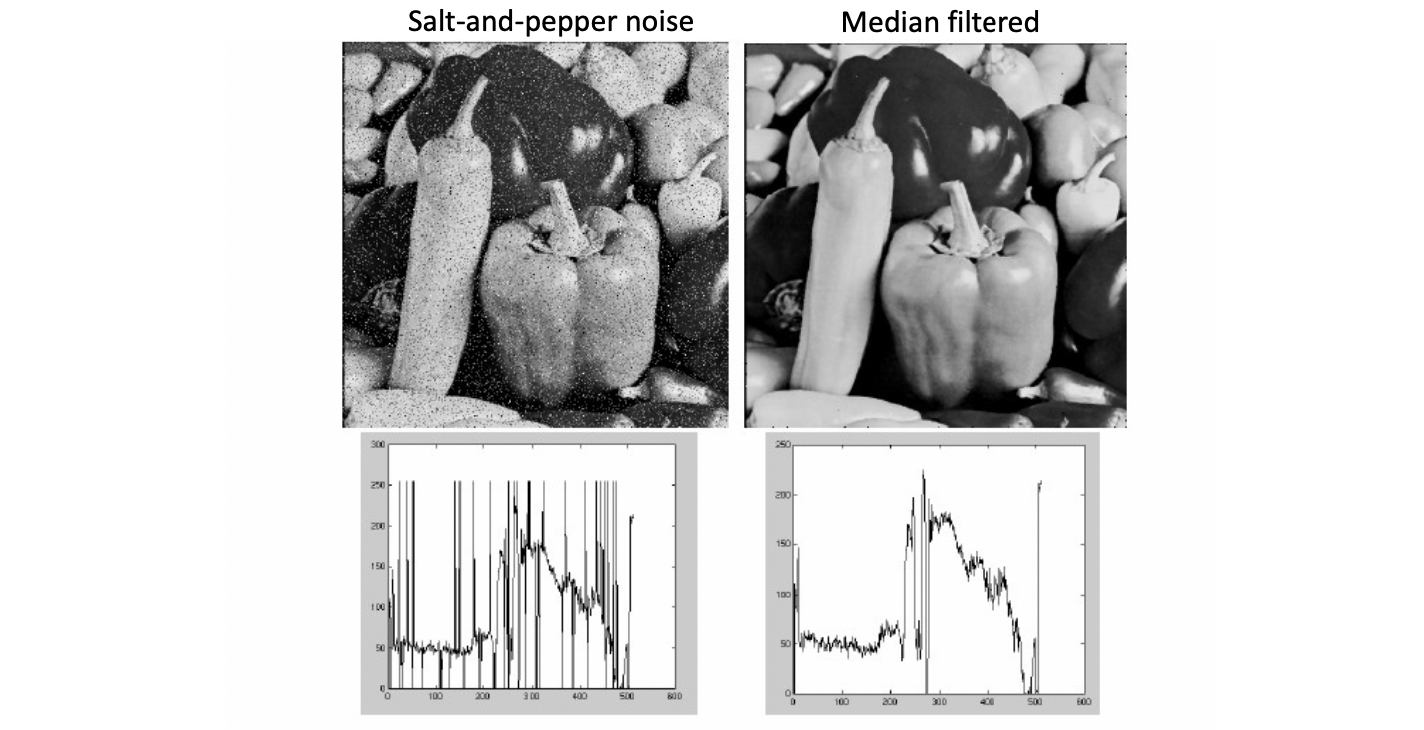
왼쪽 그림을 보면 지저분하죠? 이 노이즈가 마치 이미지에 소금과 후추를 뿌려놓은 것 같다해서 salt-and-pepper noise라 부릅니다. 바로 아래 픽셀 값을 보면 알겠지만 너무 밝고 어두운, 즉 튀는 부분들이 곳곳에 있어 이렇게 보이는 것입니다. 실제로 카메라가 오래 되서 낡게 되면 RGB 값을 저장하는데 있어 $(0, 0, 0)$이나 $(255, 255, 255)$와 같이 기록할 수 있기 때문에 이와 같은 일이 벌어집니다. 이럴 때 Median Filtering을 적용하면 오른쪽과 같이 매끄럽게 만들 수 있습니다.

위에서 보이는 것처럼, 마냥 blur 처리를 하는 Gaussian에 비해 Median은 노이즈를 제거하는 데 굉장히 효과적인 필터링 방식입니다. 추가적으로, Medain Filtering은 Linear 하진 않기 때문에 Linear Shift-Invariance Filtering에 끼지는 못합니다.😅