이전 글에 이어서 Image Filtering에 대해 계속해서 공부하도록 합시다.

Convolution

나중을 위해 Convolution(합성곱)에 대해 알아보고 넘어가도록 합시다. 위키백과에서 말하는 합성곱의 정의는 다음과 같습니다.

합성곱이란 하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음, 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자이다.

이를 수식으로 표현하면 아래와 같습니다.

$(f*g)(x) = \int_{-\infty}^{\infty}f(y)g(x-y)dy$

하나를 기준으로 나머지 다른 함수가 이동하면서 겹치는 영역을 곱해서 적분한 값이죠. 말이 조금 어렵긴 하지만, 구글에 검색해서 애니메이션으로 보시면 이해가 빠르실 겁니다. 위의 식은 변수가 $x$ 하나로 1D이며 적분을 하기에 Continous하지만, 우리가 적용하고 싶은 픽셀은 변수가 $x$축 하나, $y$축 하나 총 2개의 2D이며 또한 Discrete 합니다. 이를 수식으로 표현하면 아래와 같습니다.

$(f*g)(x,y) = \sum_{i,j=-\infty}^{\infty}f(i,j)I(x-i, y-j)$

여기서 차례대로 결과값 $(f*g)(x,y)$는 필터링된 이미지, $f(i,j)$는 필터, $I(x-i, y-j)$는 인풋 이미지를 의미합니다. 만약에 필터의 크기가 $3\times3$이라면 합의 범위가 $\sum_{i,j=-1}^{1}$이 되면 됩니다. 이제 위의 수식을 다시 보니 어떤가요? 우리가 지금까지 했던 Box Filtering과 같은 연산처럼 보이지 않나요? 맞습니다. 필터링을 Convolution으로 표현할 수 있는 것이지요. 엄연히 얘기하면 Convolution은 위와 같이 $x-i,y-j$를 취하기 때문에, 이미지의 픽셀 값과 필터의 값이 대칭 관계에 있는 것끼리 곱하기 때문에 완전히 같지는 않습니다. 그것은 아래와 같은 수식으로 표현할 수 있으며,

$(f*g)(x,y) = \sum_{i,j=-\infty}^{\infty}f(i,j)I(x-i, y-j)$

이를 Cross-Correlation이라 부릅니다. 아래 그림과 같이 Convolution은 상화좌우로 반전된 Cross-Correlation이라 표현할 수 있는 것이지요.

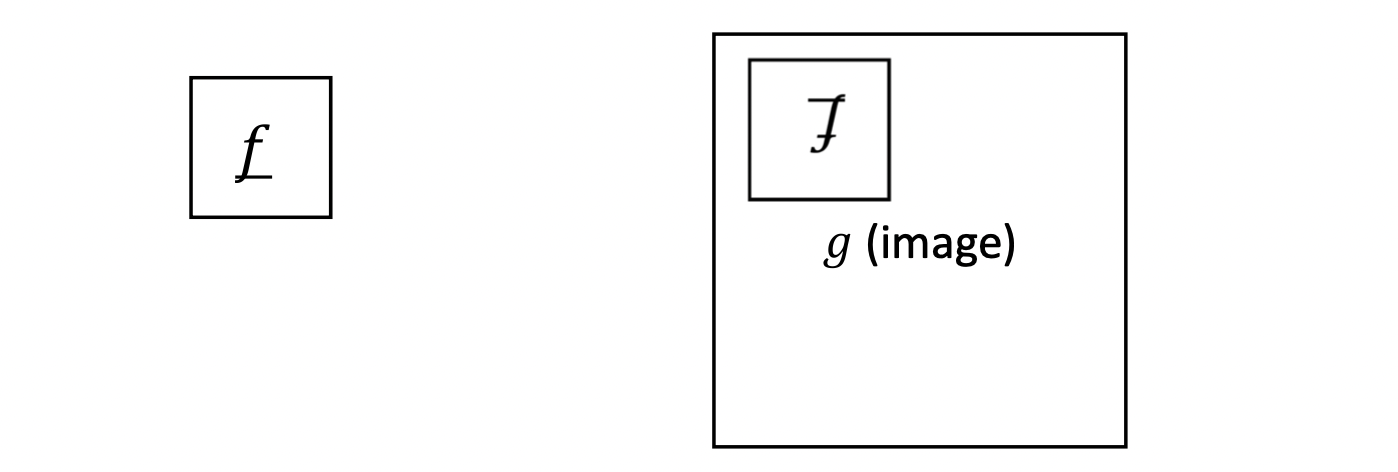
Convolution은 또한 다음과 같은 속성도 지닙니다.

• Community : $f*g=g*f$
• Associativity : $f*(g*h) = (f*g)*h$
• Distributivity : $f*(g+h) = (f*g) + (f*h)$
• Associativity with scalar multiplication : $a(f*g) = (af)*g$
• Differentiation : $\frac{d}{dx}(f*g)=\frac{df}{dx}*g=f*\frac{dg}{dx}$

이 중에서는 Associativity가 굉장히 유용하게 사용됩니다. 왜냐하면 어떤 $f$라는 필터를 적용할 때 $f_1*(f_2*(f_3*g)))$로 순차적으로 적용할 필요없이 이것이 $(f_1*f_2*f_3)*g$와 같다는 점을 이용하면 $f_1*f_2*f_3$를 미리 계산하여 계산을 훨씬 빠르게 할 수 있습니다.

Image Gradients

다시 한 번 이미지를 픽셀 값의 그래프로 나타낸 것을 확인해봅시다.

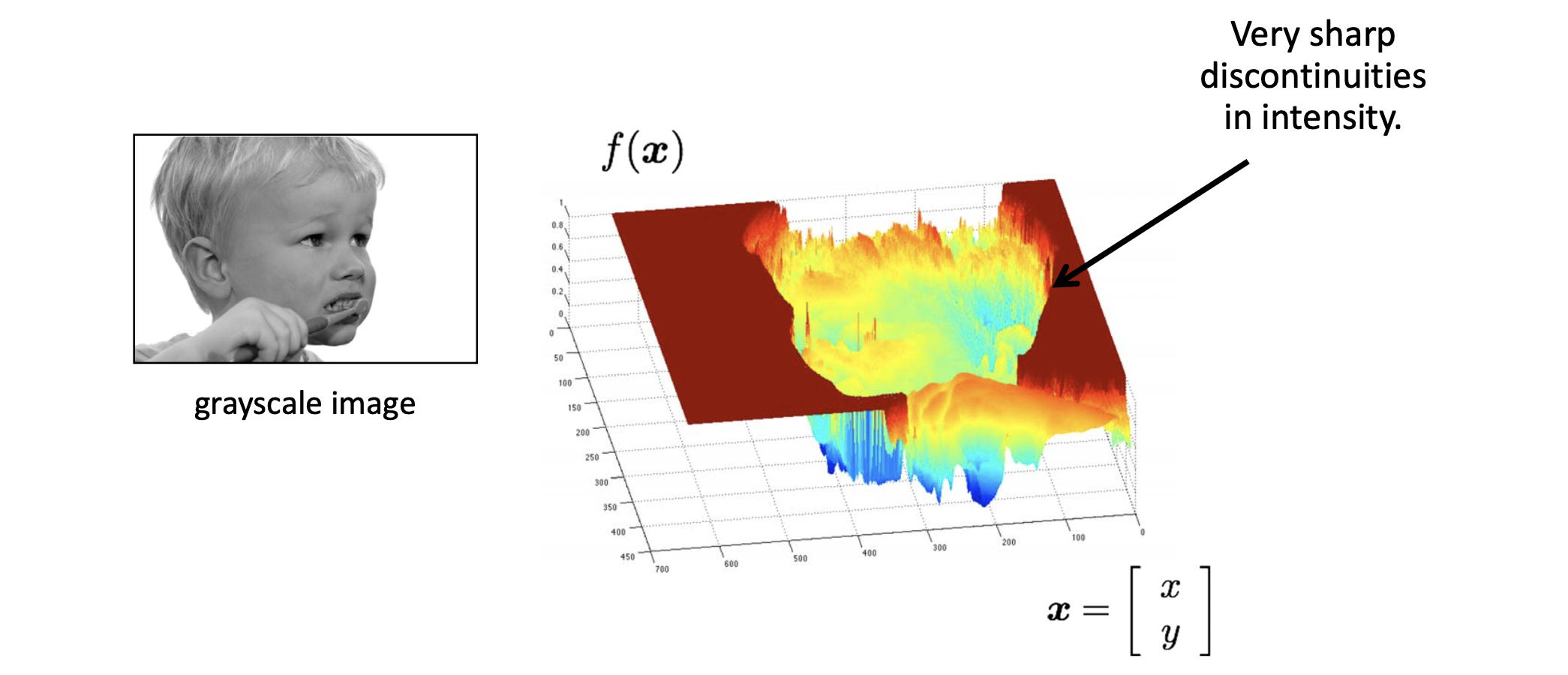
여기서 픽셀 값이 급하게 바뀌는 부분을 edge라고 표현합니다. 색깔이 확 바뀌는 부분, 윤관선이라고 표현할 수도 있겠지요? 이런 곳을 보면 특징적인 것이 Discontinuity, 즉 값이 불연속적인 부분이라는 것입니다. 우리 어떤 값이 불연속인 점이 지점인지를 확인하고 싶을 때 무엇을 활용하였죠? 바로 미분입니다. 다시 한 번 상기해볼까요?

$f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$

그런데 우리가 하고 적용하고 싶은 이미지는 뭔가요? Discrete 한 값이죠?? 그렇게 때문에 어쩔 수 없이 $\lim$을 빼고 $h$를 2로 하자해서 다음과 같은 식이 나오게 됩니다.

$f'(x)=\frac{f(x+1)-f(x-1)}{2}$

위와 같은 식을 적용할 수 있는 Convolution Kernel은 다음과 같을 겁니다.

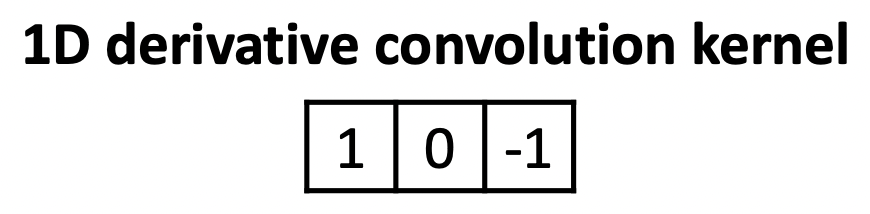
Convolution은 우리에게 익숙한 Cross-Correlation과 반대기 때문이죠. 이제 이 커널을 적용해볼라 하니 또 새로운 문제가 생깁니다.

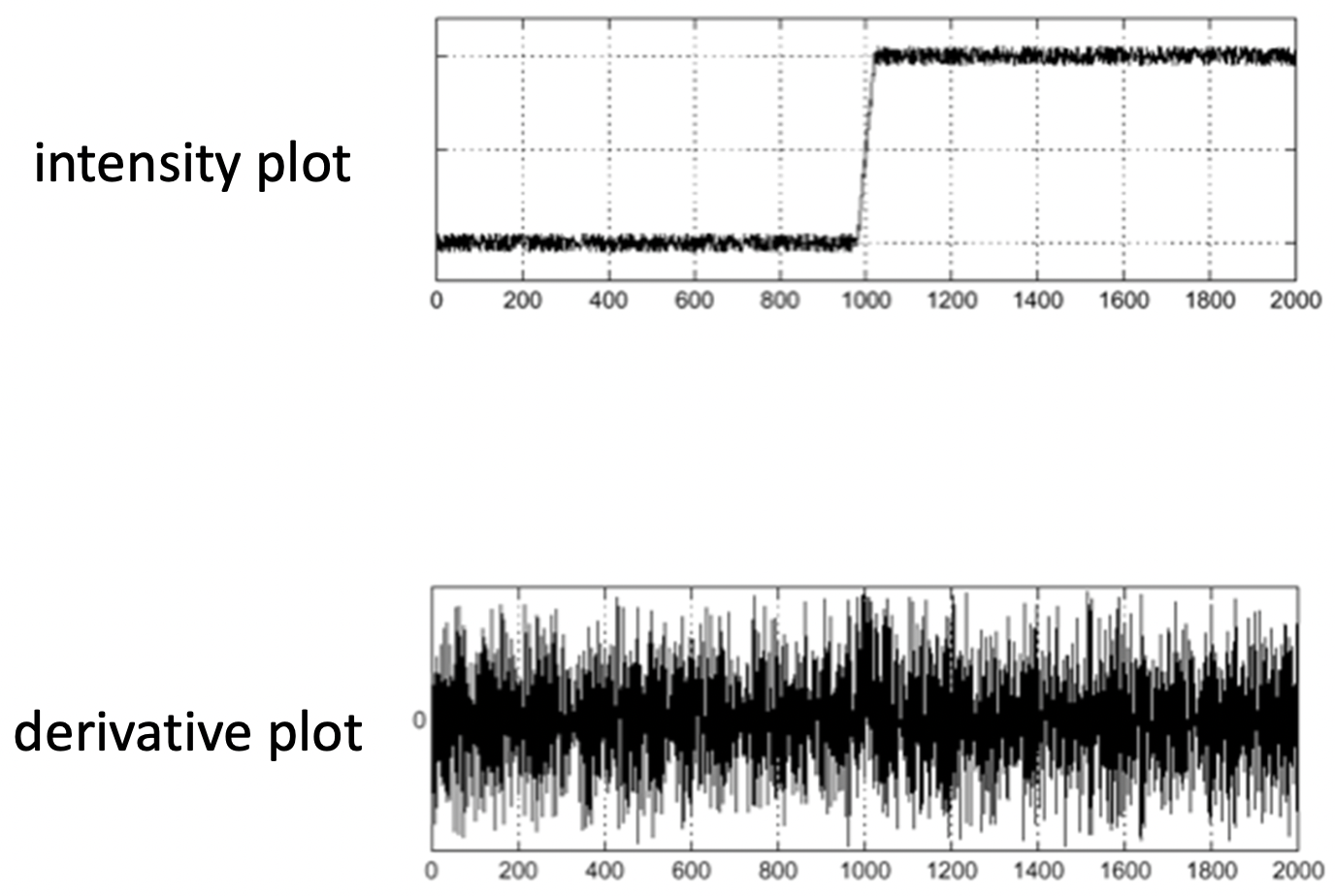
실제 이미지에는 위와 같이 타닥타닥 튀기는 노이즈들이 많아서 이들을 미분해버리면 아래와 같이 모든 구간에서 미분값이 엄청 크게 나타나 버리는 겁니다. 그래서 우리는 미분을 하기 전에 노이즈 제거를 위해 (예를 들어 Gaussian을 사용해서) blur 처리를 먼저 하자는 것입니다. 그러면 아래와 같이 깔끔하게 값을 도출할 수 있습니다.

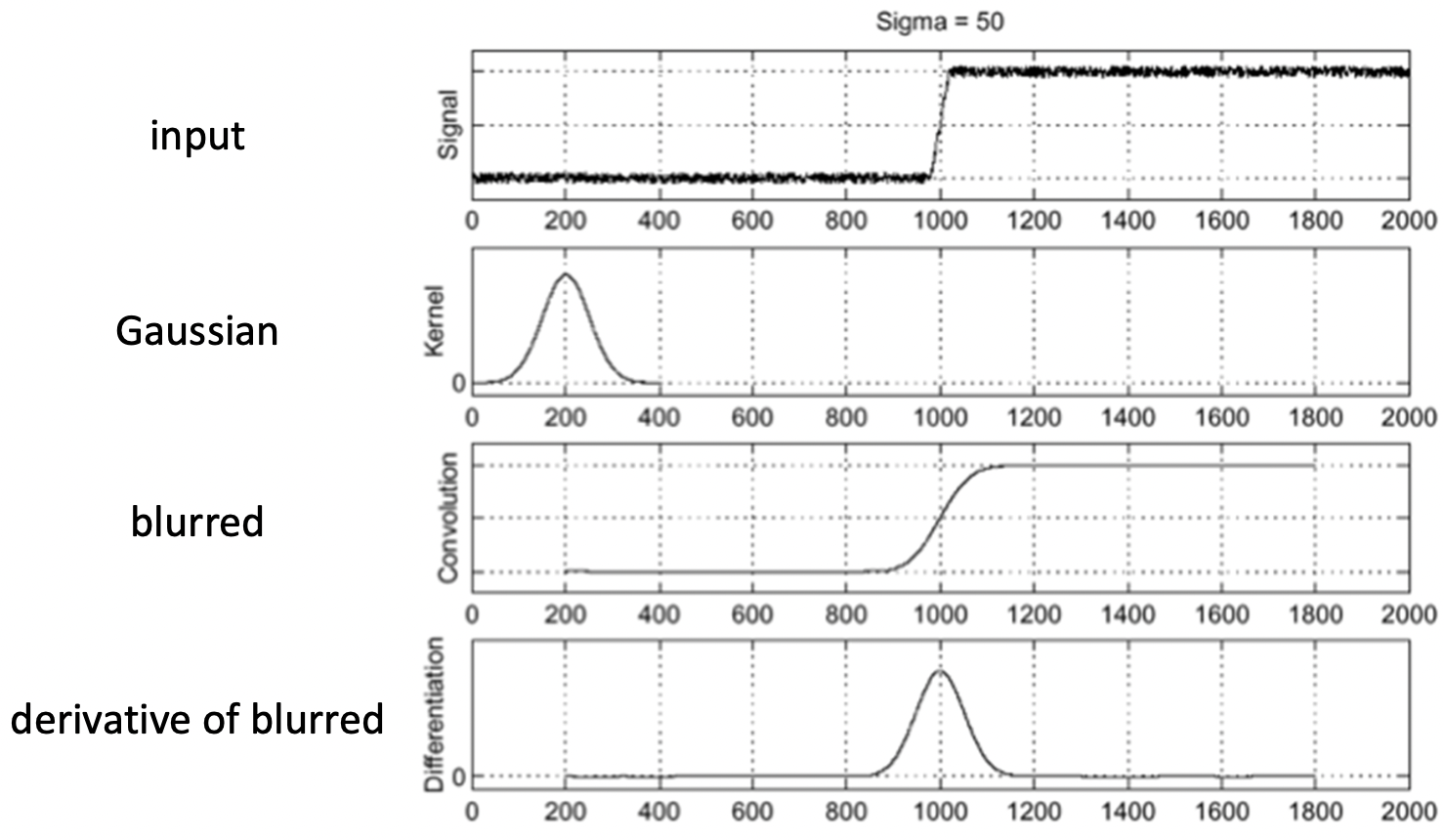
그런데 우리가 바로 방금 전에 Convolution의 가장 강력한 속성이 뭐라고 헀죠? Associatvity 입니다. 이를 이용해서 blur 처리를 커널과 derivative(미분)을 하는 커널을 미리 합성곱하여 새로운 필터, 즉 커널로 만들 수가 있게 됩니다. 그 결과는 아래와 같고 만들어진 이 커널을 Sobel convolution kernel이라고 합니다.

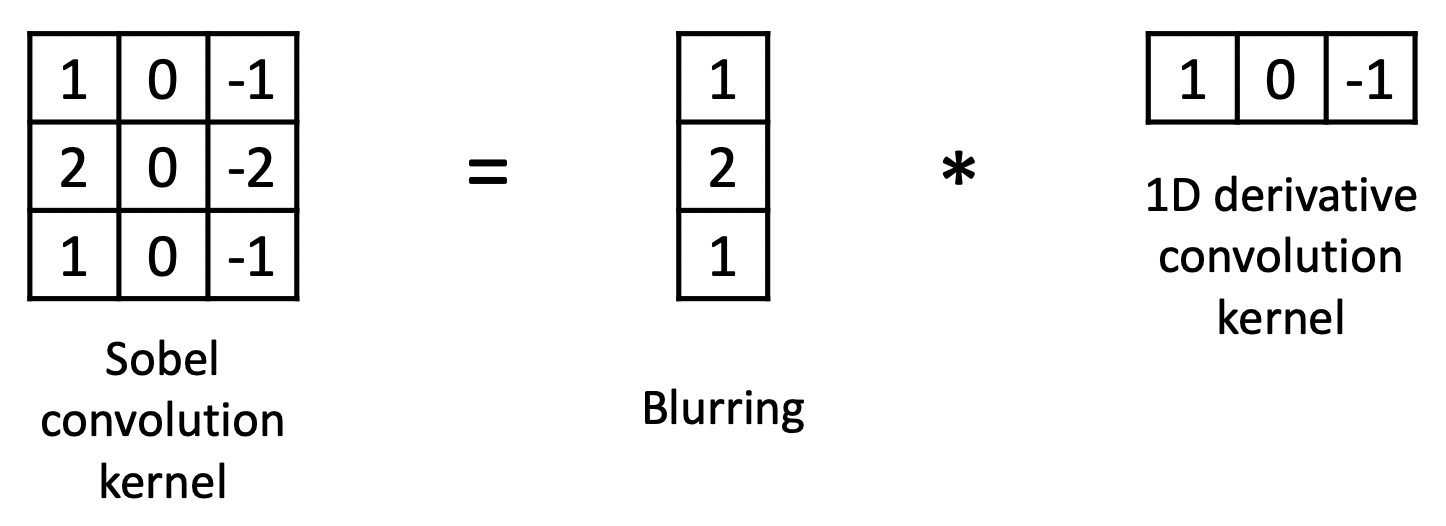
세로 축으로 blur 처리를 하고 그 값을 가지고 $x$ 방향으로 미분하기 때문에 이는 Vertical 라인을 잡아내는 필터라고 할 수 있습니다. 반대로 $y$ 방향으로 미분하는 Horizontal 라인을 잡아내는 필터를 만들고 싶다면 Communitiy 속성을 추가적으로 이용하여 아래와 같이 만들 수도 있습니다.

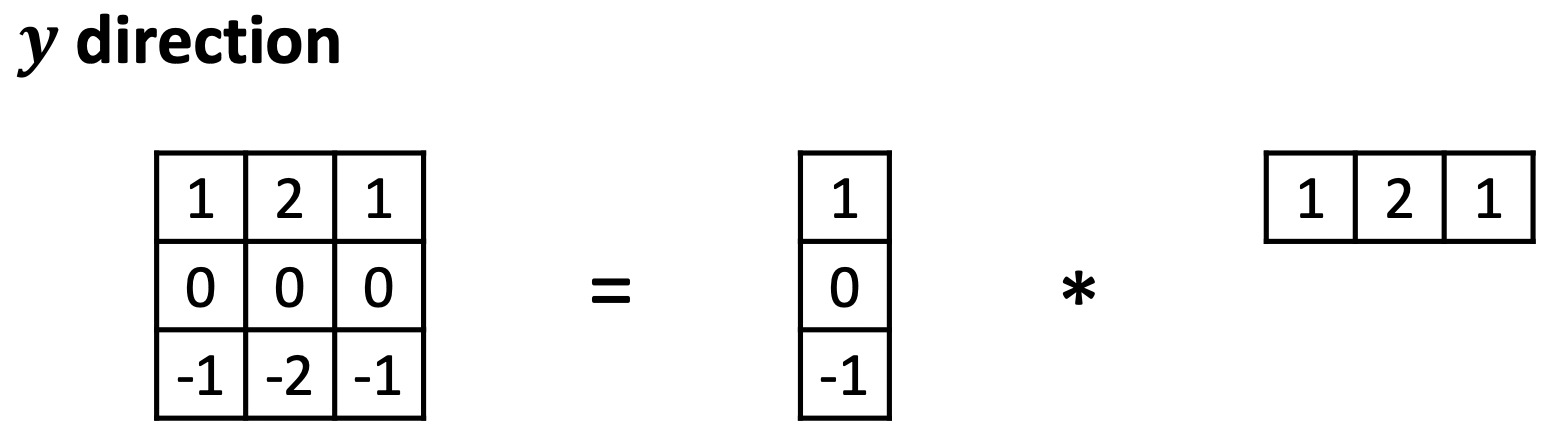
그렇게 결과적으로 $x$축과 $y$축으로의 Sobel 필터링을 적용한 모습은 아래와 같습니다. 차이가 보이시죠?

이제 실제로 Image Gradients를 구하여 봅시다. 이미 설명들였던 대로 각각 $x$ 방향과 $y$ 방향으로 derivative 필터를 선택합니다. 저는 공부하였던 Soble 필터를 선택하겠습니다.

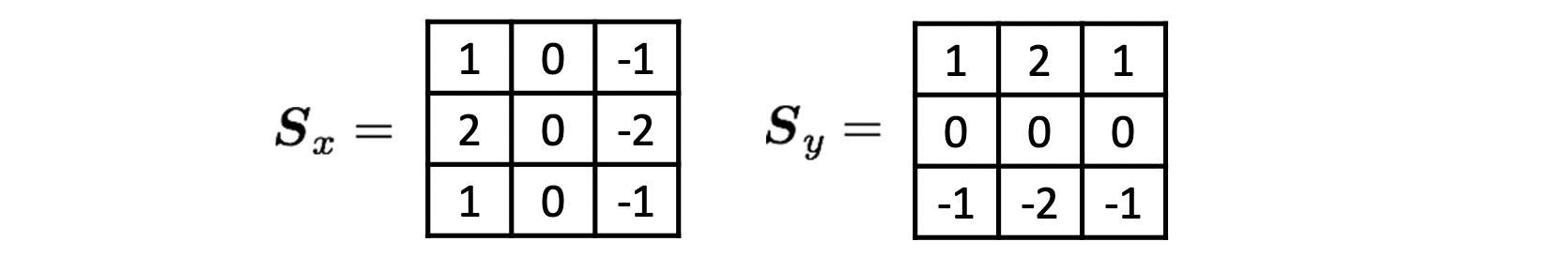
이 후에는 이 필터링을 적용하여 각각 $x$축과 $y$축 방향으로 미분한 값들을 구합니다.

이 값들을 통해서 우리는 실제 gradient(기울기)는 물론이고 edge의 방향 및 크기까지 도출할 수가 있습니다.

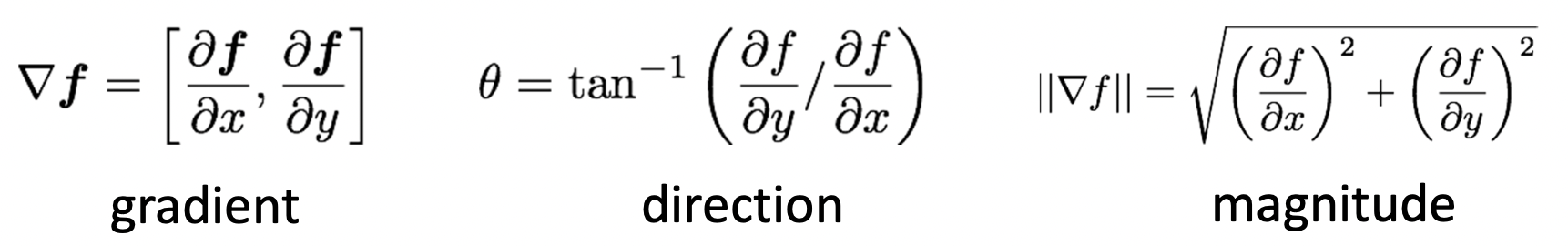
이를 적용한 예시는 아래와 같습니다. 느낌이 오시죠??

Edge Detector

그래서 우리가 이 점을 이용하면 아래와 같이 윤곽선을 추출해주는 Edge Detector를 만들 수 있을 겁니다.

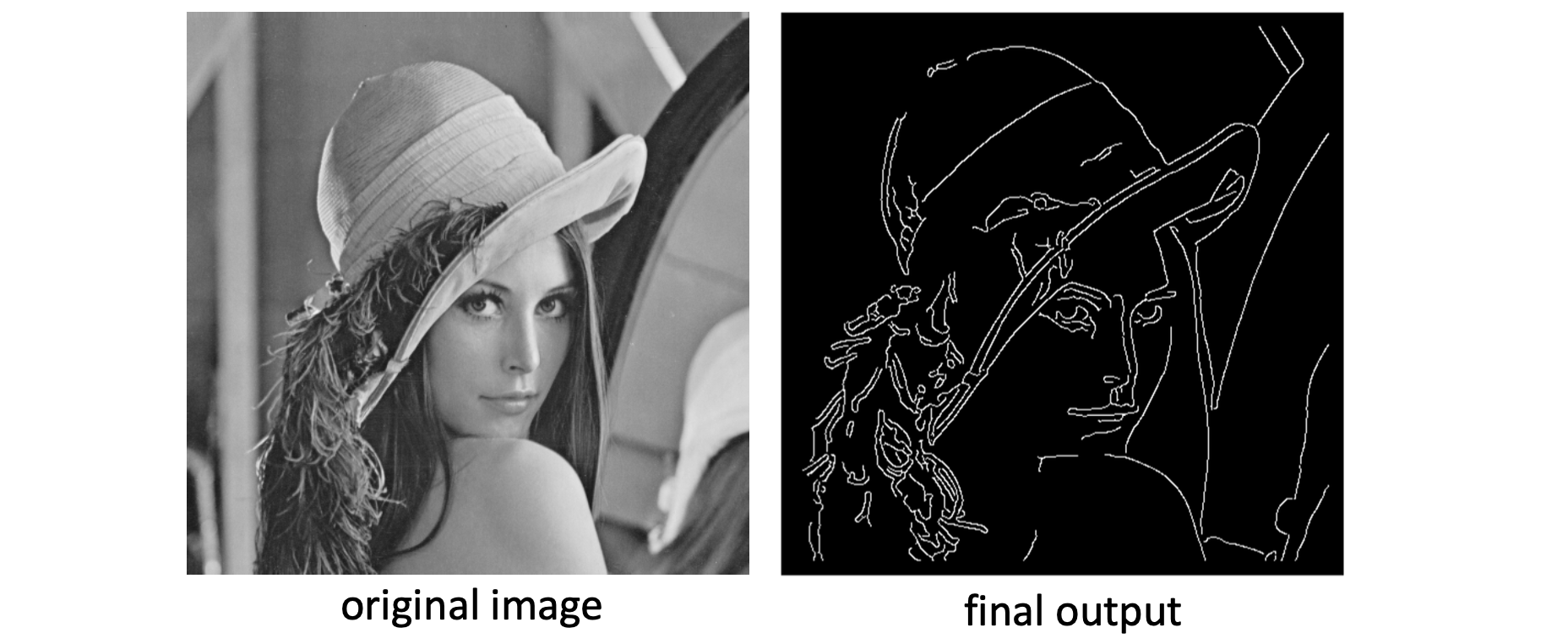
위의 오른쪽과 같은 결과를 가지기 위해 몇 가지 과정을 거쳐봅시다. 첫 번째는 방금 공부했던 gradient 를 적용하여 그것의 크기를 픽셀 위에 그대로 나타내면 아래의 왼쪽과 같은 이미지가 나오게 됩니다. 불필요한 부분도 나타나서 뚜렷하지 않고 이미지가 번지기 때문에, 그 크기가 작은 부분은 처내는 Thresholding 을 거쳐서 오른쪽과 같은 이미지가 나오게 됩니다. 그런데 오른쪽을 보면 이제는 그 크기의 차이 때문에 선들의 굵기가 일정하지 않다는 문제가 생기게 됩니다. 그래서 우리는 노란색 네모 박스와 같은 굵은 선들을 얇은 선으로 처리하고 싶습니다.

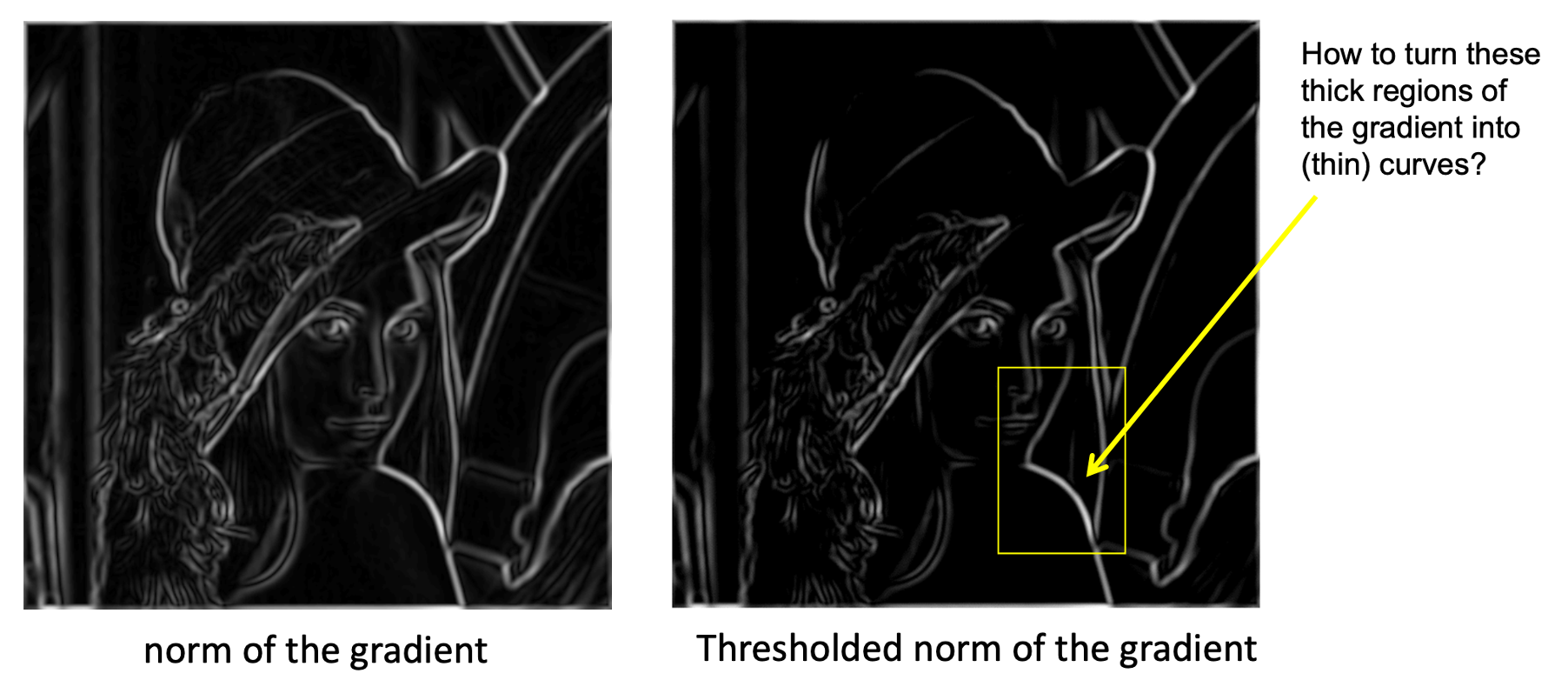
이 때, 사용할 수 있는 방법 중에 하나가 바로 Non-maximum Suppression(NMS)입니다. 현재 우리가 윤곽선을 처리한 과정을 보면 아래 왼쪽 두 그림과 같습니다. 실처럼 생긴 선은 해당 픽셀에서의 gradient 를 의미하는 것이죠.

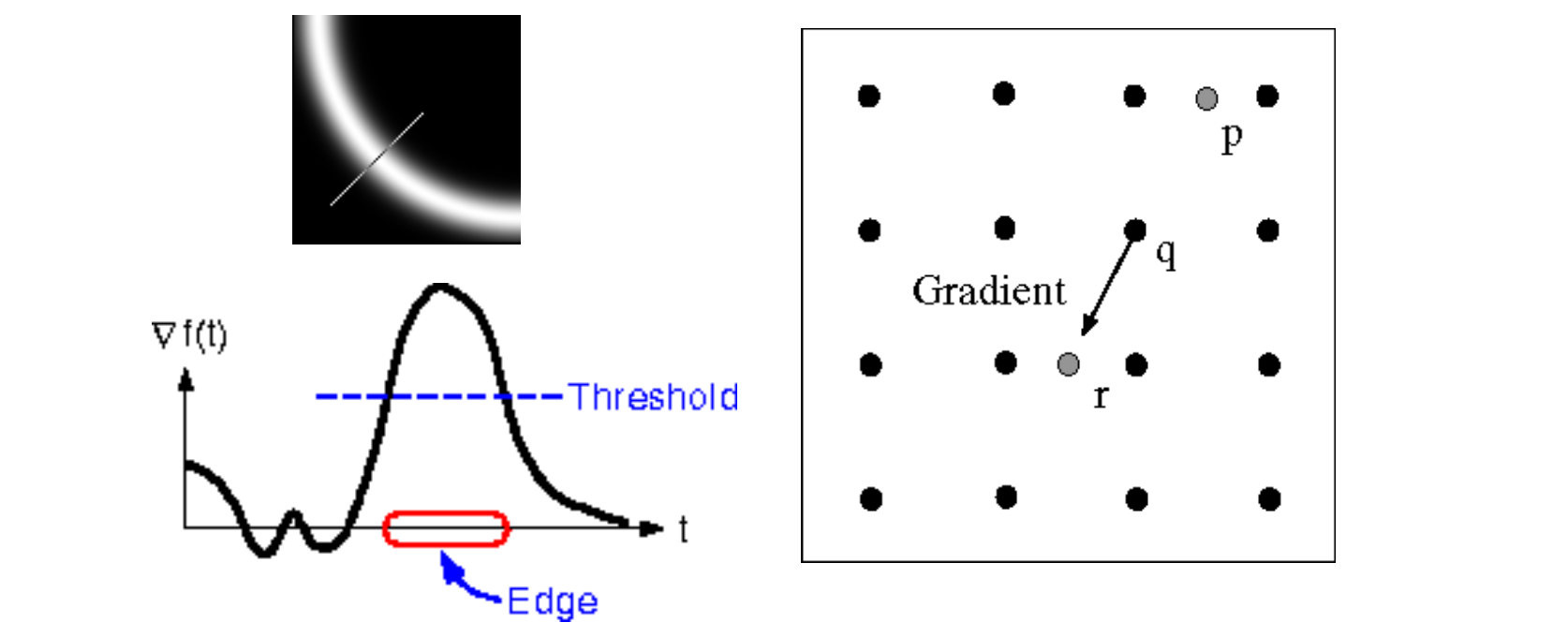
핵심은 이 gradient 상에 표시된 픽셀들 중 몇 가지를 제거해야 한다는 것입니다. 오른쪽 그림을 보면 각 점들은 각각의 픽셀의 중앙값, 즉 center pixel value 를 의미합니다. 현재 픽셀값은 gradient 의 크기일 것입니다. 현재 보정하고 싶은 픽셀을 q라고 합시다. 최대인 픽셀만을 남기기 위해 q와 gradient 상의 이웃인 p와 r에 해당하는 픽셀값보다 q가 작다면 q를 지우는 겁니다. (그림과 같이 p와 r은 center piexel 이 아닐 수 있기 때문에 내분점 등을 도입해서 이를 정의해주는 과정은 필요합니다.) 그렇게 보정한 결과는 아래와 같습니다.

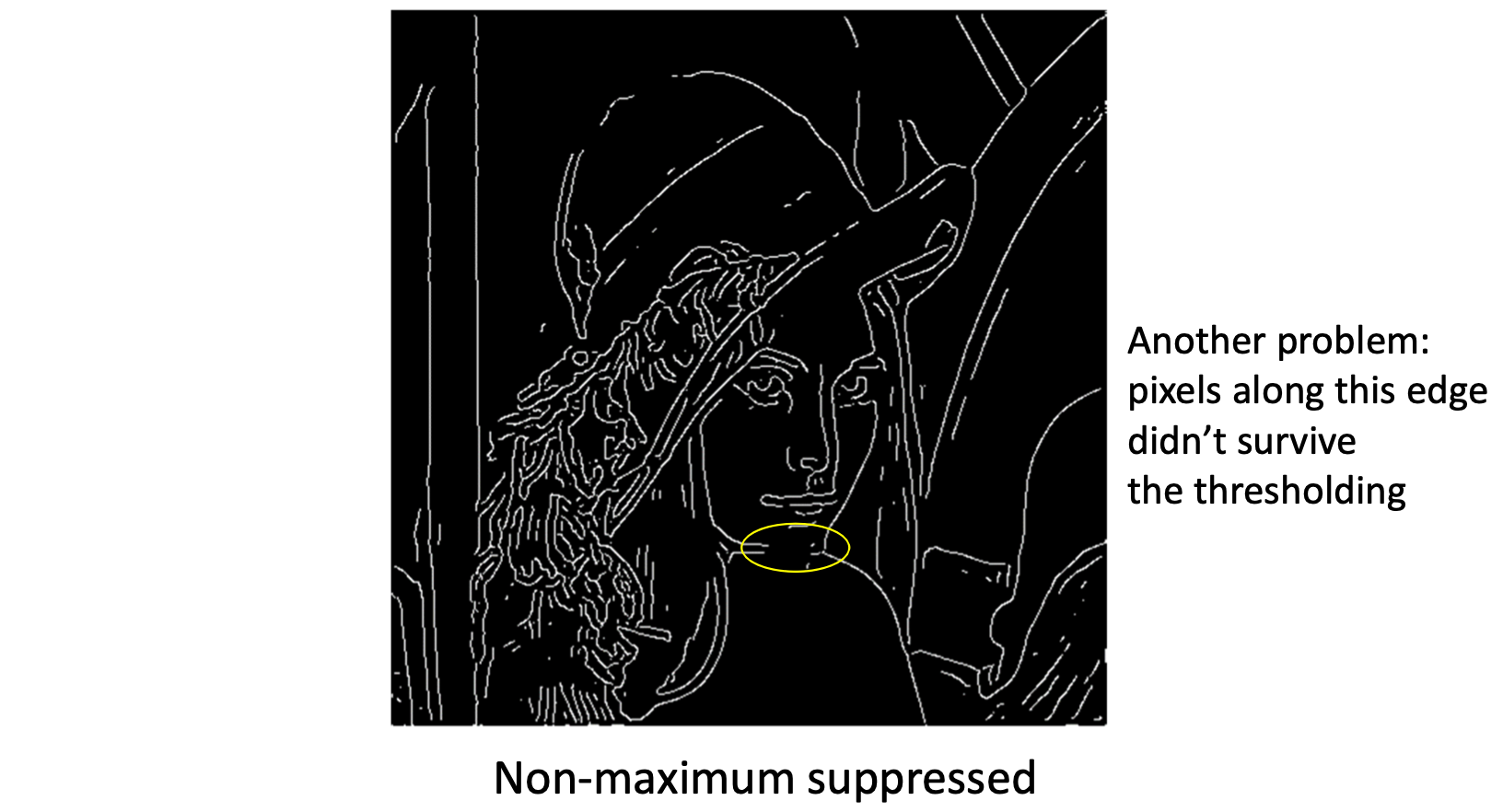
그런데 문제가 있습니다. 꼭 있어야 할 턱라인이 thresholding 에 의해서 표시되지 않은 겁니다. 사람의 눈으로는 보이는 윤곽선이 컴퓨터는 픽셀 값이라는 수치로 계산하다 보니 이와 같은 일이 벌어질 수 있는 것이죠. 그래서 우리는 아래 그림과 같이 필요하다면 선과 선 사이를 이어주는 과정이 필요합니다.

Hysteresis Thresholding은 간단하게 말해서 실제 값이 Threshold 보다 작더라도 바로 옆에가 크다면 이를 반영해주는 기법을 의미합니다. 물론 heuristic 한 방법이기 때문에 항상 반례가 존재합니다. (무조건적으로 이상적인 결과를 도출해주진 않습니다.)

그래도 다음과 같이 threshold를 낮게 적용해버린다면 실제로는 edge가 아닌 부분까지 골라내서 결과가 매우 지저분해지게 됩니다. 그래서 먼저 높은 threshold를 주고 설명드린 hysteresis threshold 를 적용하는 방법이 훨씬 효과적인 결과를 도출해내게 되는 것입니다.

Derivative of Gaussian(DoG) Filter

다시 한 번, image gradient 를 상기해 봅시다. 기존 인풋 이미지에 Gaussian 을 사용해서 blur 처리를 해서 노이즈를 제거 해준 뒤 이를 derivative (미분) 해주었습니다.

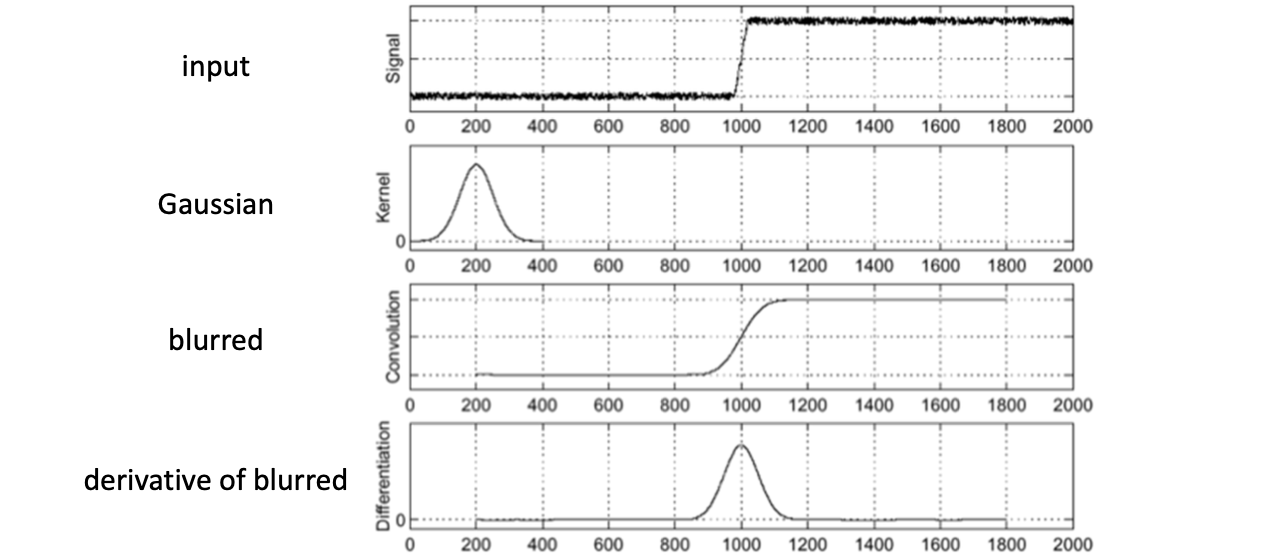
그런데, 우리는 다음과 같은 Convolution 의 속성을 압니다.

$\frac{d}{dx}(h*f) = (\frac{d}{dx}h)*f$

위에서 $f$는 인풋 이미지일 것이고, $h$를 Gaussian이라 해봅시다. 그러면 우리는 미리 Gaussian 자체를 미분해놓아서 이를 인풋 이미지들에 적용함으로써 훨씬 더 빠르고 효율적으로 필터링할 수 있을 것입니다.

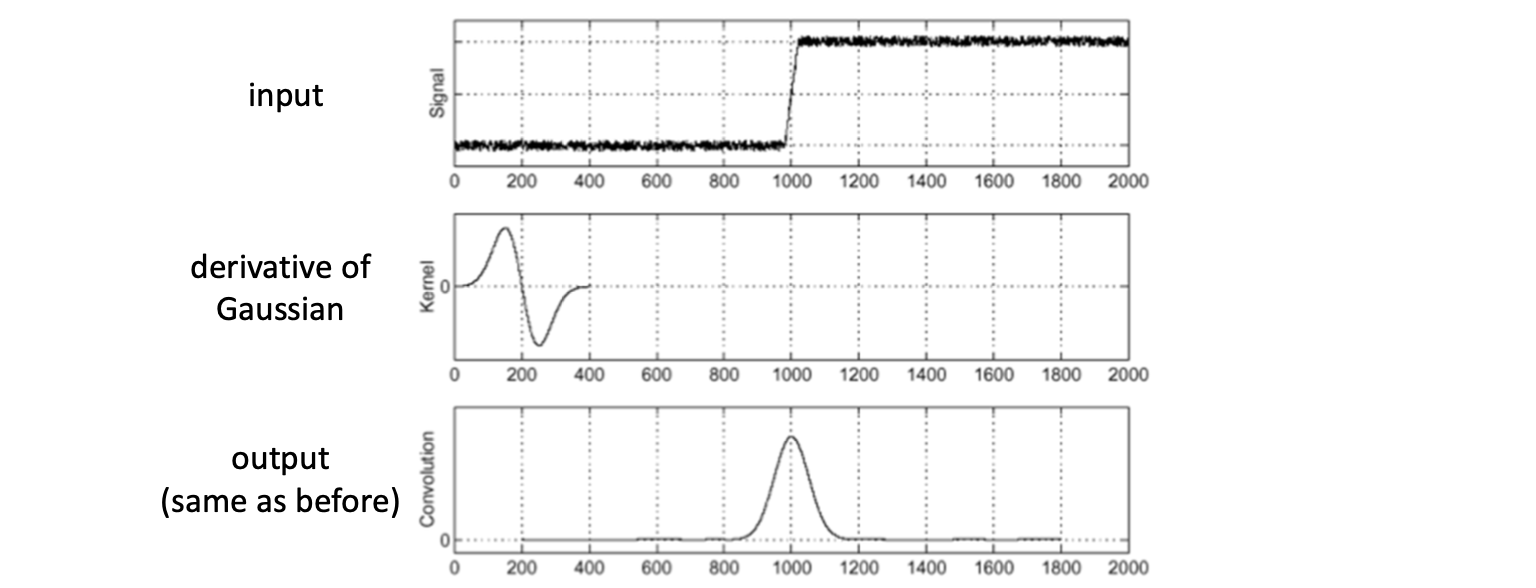
그 결과는 위와 같습니다. derivative of Gaussian 이 input을 왼쪽부터 주루루룩 이동해가며 적용한 결과는 전과 같은 것이죠. 따라서 이와 같은 필터를 Derivative of Gaussian(DoG) Filter 라고 부릅니다.

Laplace Filter

일차 미분 필터가 있으면 이차 미분 필터도 존재하지 않을까요? 아래와 같이 이계도함수를 위한 필터를 Laplace Filter라고 합니다.

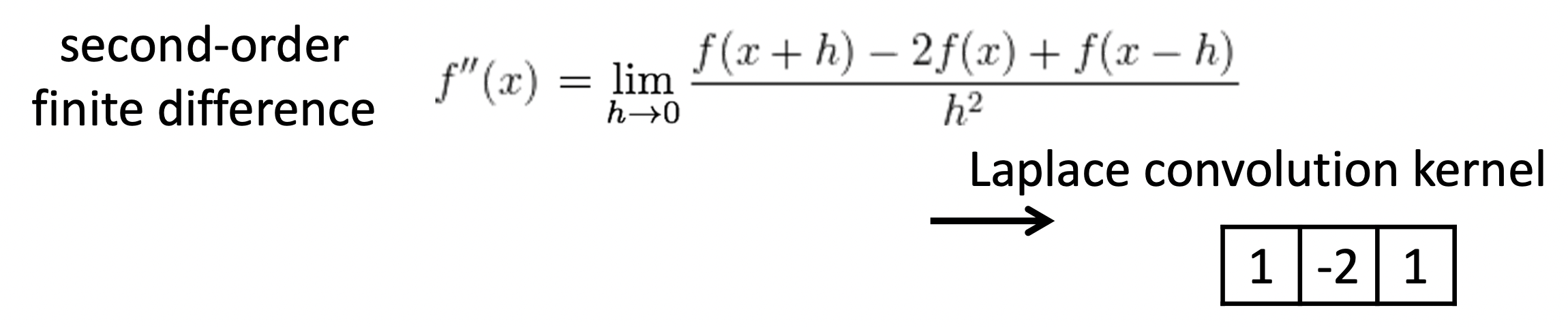
바로 위 DOG Filter 에서 했던 것과 마찬가지로, $\frac{d^2}{dx^2}(h*f) = (\frac{d^2}{dx^2}h)*f$ 인 점을 이용해서 Gaussian 자체에 먼저 이차 미분을 적용한 필터를 우리는 Laplacian of Gasussian(LoG) Filter 라고 합니다.

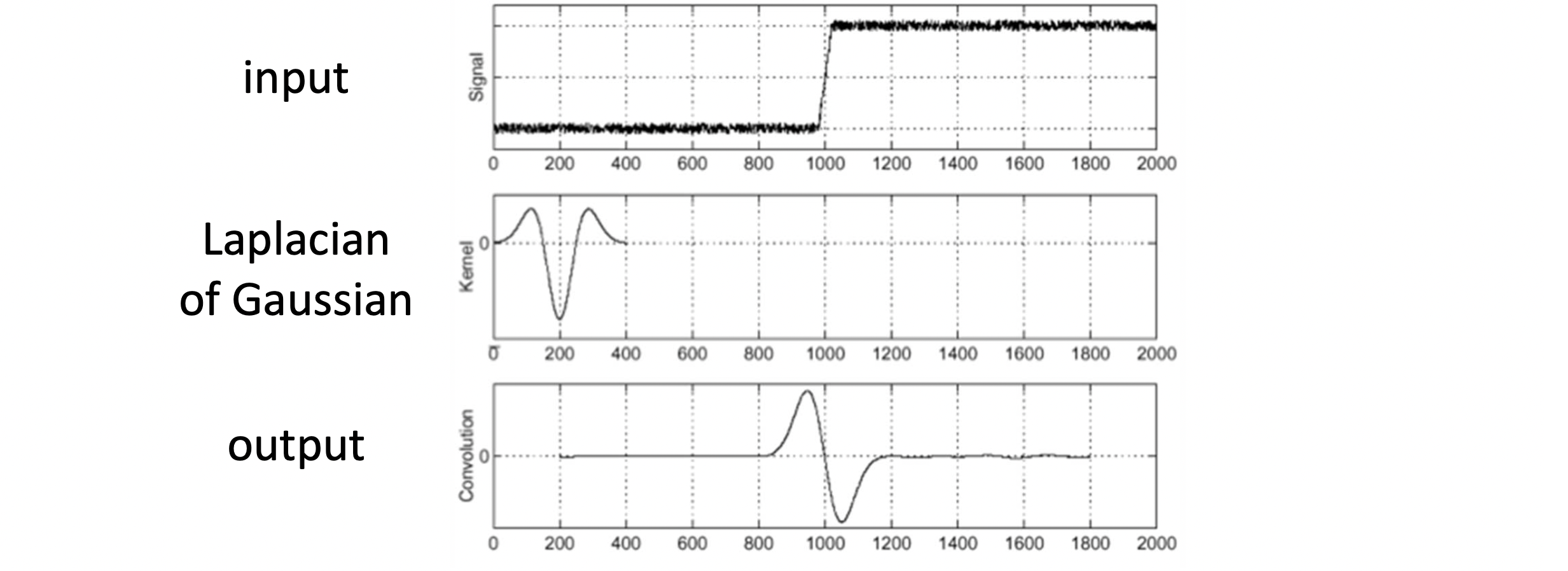
최종적으로 LoG Filter 를 적용한 결과에서 edge 에 해당하는 좌표 1000의 값을 보면 0인 것을 확인할 수 있습니다. 이렇게 0을 기점으로 양쪽이 값이 반대로 교차하는 Zero Crossing을 확인할 수 있습니다. edge를 기준으로 양 방향의 극값을 찾는 LoG 와 edge에 해당하는 하나의 극값을 찾는 DoG 에 대한 차이는 아래의 결과를 보면 확실히 와닿으실 수 있을 겁니다.

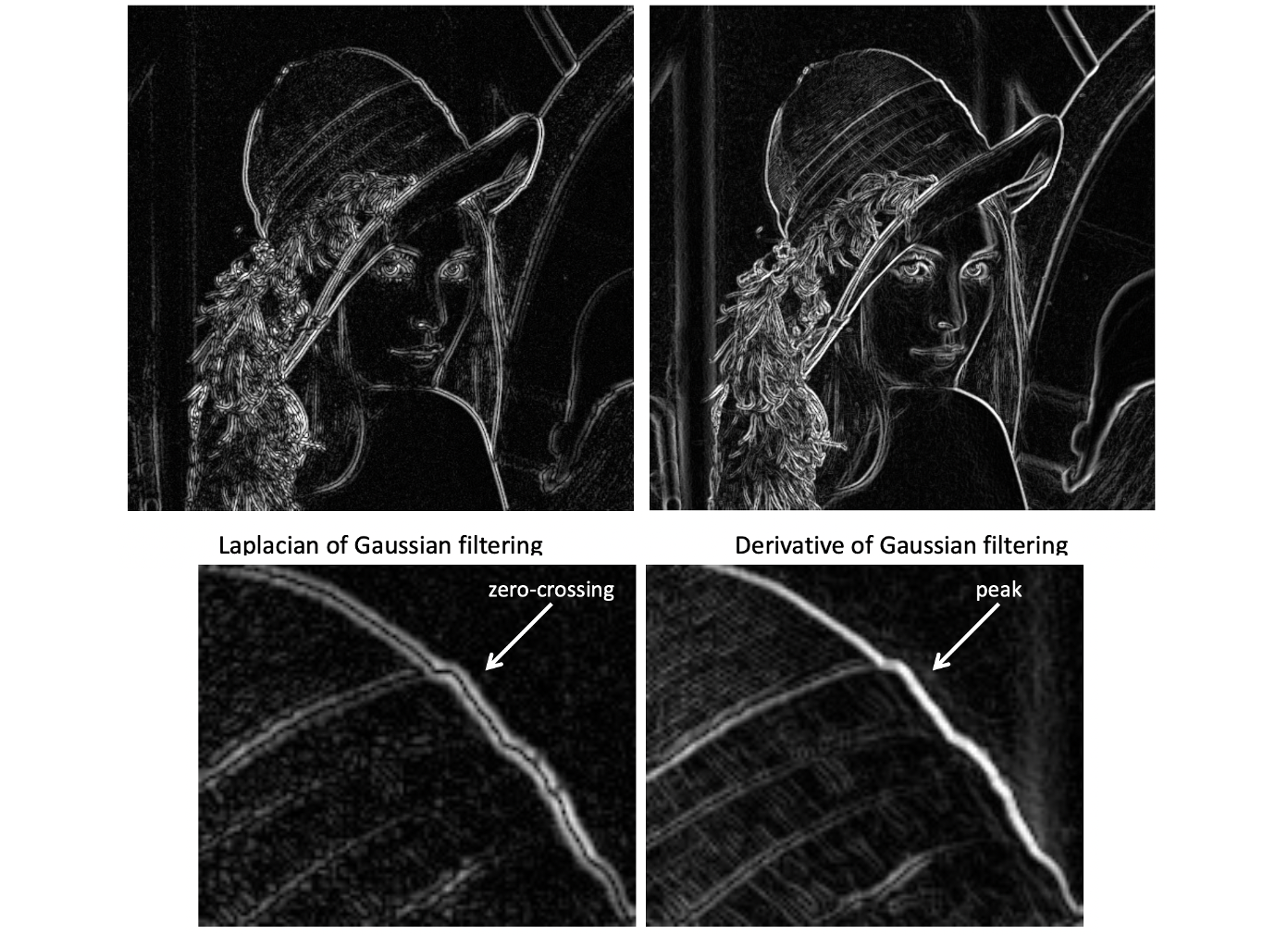
일반적으로, 기준이 하나가 아닌 두 개가 되는 Zero-Crossing 이 일반적으로 edge의 위치를 구별하는 데 더 정확합니다.😊