정보량과 엔트로피 및 교차 엔트로피

내 머리가 너무 나빠서, 엔트로피와 교차엔트로피를 이해하는데 2주가 넘게 걸렸다. 아옼

정보량 I(x)

사건의 정보량이 크다는 의미, 그 사건 발생을 경험할 확률 및 빈도가 낮다라는 뜻이다.

아래 예시를 보고, 친구들과 가위바위보를 했을때 정보량을 비교해보자.

Q. 사건 A와 B중, 어떤 것의 정보량이 더 높을까?

1. A: 친구 1명과, 가위바위보를 했을때, 내가 이겼다 !
2. B: 친구 100명과, 가위바위보를 했을때, 내가 이겼다 !

친구 100명과 가위바위보를 했을때의 이길 확률이 낮으니, 사건 B의 정보량이 더 크다 (I(B) > I(A) )

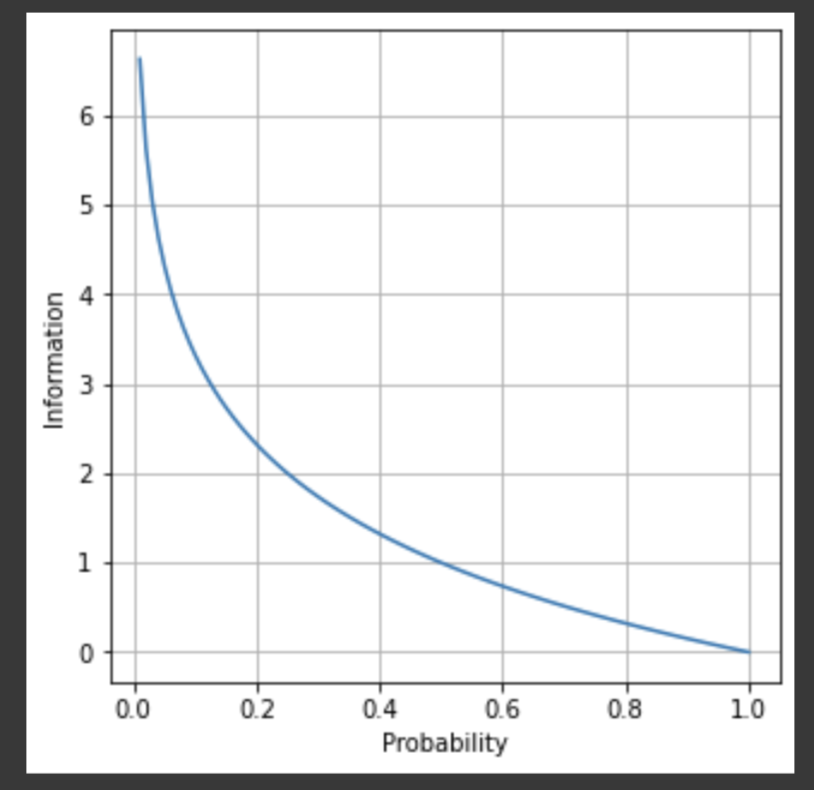
정보량은 로그 그래프가 표현한다.

$I(x) = {\log({1\over p(x)})} = {-\log(p(x))}$

# numpy와 matplot은 미리 임포트함
x = np.linspace(0,1,100)
i_x = -np.log2(x)
plt.figure(figsize = (5,5))
plt.title('Amount of Information along the log graph')
plt.plot(x, i_x)
plt.tick_params(axis="x", colors="darkgreen")
plt.tick_params(axis="y", colors="teal")
plt.grid(True)
plt.xlabel("Probability", color="darkgreen")
plt.ylabel("Information", color="teal")
plt.show()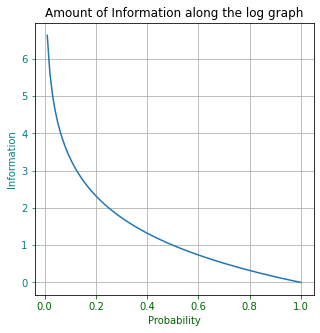

로그 그래프와 같이, 확률 p(x)가 낮을수록 정보량 I(x)가 높게 표현된다.

정보량 I(x)가 로그함수로 설명되는 이유는 아래와 같다.
1. 정보량은 항상 0보다 크다.
2. 항상 발생하는 정보량은 0이다.
3. 자주 일어나는 사건이면 (확률이 높을수록), 전달되는 정보량이 작다.
4. 각 사건이 독립적이라면, 각 사건의 합으로 표현된다. i.e) $\log {p(x_1)p(x_2)} = \log p(x_1) + \log p(x_2)$

엔트로피 H(X)

사건 A를 반복했을때 얻는, 정보량 I(x)의 기댓값 (평균 정보량)이다.

$H(x) = E(I(X) = E(\log {1\over p(x)})= -E(\log p(x))$

어떤 사건A의 확률 P(x) = [바나나: 0.5, 딸기: 0.3, 사과: 0.2] 일때,

$H(x):$
= $p(바나나|A)*\log p(바나나|A) + p(딸기|A) *\log p(딸기|A) + p(딸기|A) * \log p(사과|A)$
= $0.5 * 0.3010 + 0.3 * 0.5229 + 0.2 * 0.6990$
= 0.4417

교차 엔트로피 H(P,Q)

실제 분포와 예측 분포가 다름에 따라, 예측 분포 Q(x)를 가정하고 엔트로피 계산한다.

• Q(x): 예측
• P(x): 정답

$H(P,Q) = -\sum P_x(x)logQ_x(x) = -\sum P_x(x)logQ_x(x) + (1-P_x(x))log(1-Q_x(x))$

평균 교차 엔트로피 (CEE)

1. 교차 엔트로피는 다음의 식으로 표현한다고 했다.

   $H(P,Q) = - \sum P_x(x)\log Q_x(x) = P_x(x_1)\log Q_x(x_1) ... P_x(x_2)\log Q_x(x_2)$

2. 이산 분포(Discrete Distribution)일때, 사건 B의 확률을 표현하면 다음과 같다. 교재에서는 우도(Likelihood)를 적용한다고 한다.

   $P(B|A) = 1 - P(A|B)$ (참고: 1 = 전체 확률)

3. 우도(Likelihood)를, 교차 엔트로피 H(P,Q)에 적용하면,

   $P_x(x)logQ_x(x) = P_x(x_1) \log Q_x(x_1)$ + $(1 - P_x(x_1) \log (1-Q_x(x_1)))$

4. 발생하는 확률 $X = {x_1 .. x_n}$의 모든 교차 엔트로피에 대한 평균으로 구해보자

   $P_x(x)logQ_x(x)$ :
   = ${1 \over N}$ {$P_x(x_1) \log Q_x(x_1)$ + $(1 - P_x(x_1) \log (1-Q_x(x_1)))$ ... $P_x(x_n) \log Q_x(x_n)$ + $(1 - P_x(x_n)\log(1-Q(x_n)))$}
   = ${1 \over N}$ $\sum\limits_0^{N-1} P(x)\log Q(x) - (1-P(x))(\log(1-Q(x)))$

5. 머신러닝에서 w에대한 평가를 진행할때는 다음과 같이 정의한다.

   $E(w) = - {1 \over N} \sum\limits_0^{N-1}\{t_n \log y_n + (1-t_n) \log (1-y_n)\}$

   • 정답 $P_{x}(x_n) = t_n$
   • 예측 $Q_{x}(x_n) = y_n$로 치환한다.

이제 CEE를 사용하여, 모델 평가를 해보도록하자.

---

실습

이전 실습 코드와 연결 된다.

CEE

교차 엔트로피 함수 CEE_logistic(w,x,t)로 매개변수 w, 입력 데이터 x 그리고 정답값 t을 받는다.

w=[1,1]일때, CEE 공식을 통해 모델을 평가하자.

# Cross Entropy Error 함수 
def cee_logistic(w, x, t): 
  # y = 예측값, t = 정답값 
  y = logistic(x,w)
  cee = 0

  for n in range(len(y)):
    cee = cee - (t[n] * np.log(y[n])+ (1 - t[n]) * np.log(1 - y [n]))

  cee = cee / X_n
  # print("Minimized CEE:{}".format(cee))
  return cee

# test

W = [1, 1]

cee_logistic(W, X, T)

오차 값은 다음과 같다.

1.0288191541851066

CEE 경사 하강법

교차엔트로피의 경사 하강법을 통해, 최적화된 $w_0$ 및 $w_1$을 구해본다.
일반 경사하강법과 동일하게, $w_0$와 $w_1$에 대한 미분을 수행후, 다음 $w_0$, $w_1$을 구한다.

1. ${\partial E \over \partial w_0} = {1 \over N} \sum\limits_{N=0}^{N-1} (y_n -t_n)x_n$ | $w_0$에 대한 편미분
2. ${\partial E \over \partial w_0} = {1 \over N} \sum\limits_{N=0}^{N-1} (y_n -t_n)x_n$ | $w_1$에 대한 편미분

# 평균 교차 엔트로피 오차 미분
def dcee_logistic(w, x ,t):   
  y = logistic(x, w)
  dcee = np.zeros(2)
  w0 = 0 # Partial Derivate for w0 
  w1 = 0 # Partial Derivate for w1 

  for n in range(len(y)):
    w0 = w0 + (y[n] - t[n]) * x[n] # Regression에서 경사하강법은 감소하는 방향(w0 - something)으로 진행되는데, 왜 교차 엔트로피는 증가((w0 + something))하는 방향으로 갈까..? 우도때문에?
    w1 = w1 + (y[n] - t[n])

  dcee[0] = w0
  dcee[1] = w1 

  dcee = dcee / X_n
  return dcee 

W = [1,1] 
dcee = dcee_logistic(W,X,T)
print(dcee[0], dcee[1]))

모델 Fit 함수

scipy의 minimize로, 로지스틱 회귀모델을 fit한다.

앞에서, cee_logistic과, dcee_logistic을 사용하여 최적 w 값을 찾아낸다.

# The solution with the Gradient Descent of Logistic Regression 

from scipy.optimize import minimize 

def fit_logistic(w_init, x, t):
  res1 = minimize(cee_logistic, w_init, args = (x,t), \
                  jac = dcee_logistic, method = "CG")
  # 목적함수: 교차 엔트로피 함수 (cee_logistic)
  # 미분함수: jac = dcee_logistic 
  # 경사 하강법: "CG" 켤레 기울기법 (Conjugate Gradient Method)

  return res1.x

메인 함수

w 초기값을 임의로 정한뒤, fit_logistic 함수의 minimize를 사용하여, cee dcee를 통해 최적의 w를 찾는다.

plt.figure(1, figsize = (3,3))
W_init = [1, -1]

#실제 최적화된 w를 구하는 곳 
W = fit_logistic(W_init, X, T)
print("w0= {0: .2f}, w1= {1: .2f}".format(W[0], W[1]))

w를 fit하는동안 cee가 ~0.52 $\rightarrow$ ~0.25까지 떨어지고 최종 가중치가 $w_0 = 8.18$ $w_1 = -9.38$로 최적화 되었다.

Minimized CEE:0.5281568279392757
게속.. 
Minimized CEE:0.25104485295843465
Minimized CEE:0.2510446337942391
w0=  8.18, w1= -9.38

fit된 w를 사용하여 Decision Boundary를 로지스틱 모델에 그려보자.

# Boundary Decision with the W parameters calculated by fit_logistic function 

B = show_logistic(W)
show_data1(X,T)
plt.xlim(X_min,X_max)
plt.ylim(-.5,1.5)
plt.xlabel('weight $x$g', fontsize = 14)
plt.ylabel('label $t$', fontsize = 14)
plt.show()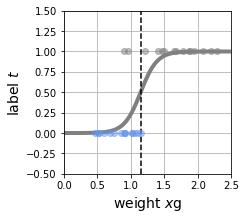

구현된 모델의 성능과, 수컷 / 암컷을 나누는 기준은 아래와 같다.
1. 교차엔트로피 (CEE) = 0.25 이고
2. Decision Boundary (B) = 1.15g

# cee는 모델을 평가하는 하나의 측도 일 뿐 ! 
cee = cee_logistic(W,X,T)
print("CEE = {0: .2f}".format(cee))
print("Boundary = {0: .2f} g".format(B))

CEE =  0.25
Boundary =  1.15 g

여러 개념이 부족하여, 2~3주가량 Classification 포스팅에 집중했는데 조금이나마 익숙해져서 다행이다.

해당실습은 1차원 특징 벡터를 사용하여 Classification을 수행했지만, 심화과정으로 2차원 특징 벡터를 이용한 2클래스 분류와 softmax함수를 사용하여 3클래스 분류를 해봐야겠다.

수고했다 혁거세 !