문제 정의
임의의 곤충의 무게 에 대해, 성별 를 예측하는 모델
= {0: 암컷, 1: 수컷}
- 입력 데이터 생성하기
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(seed = 0) # 난수 고정
X_min = 0
X_max = 2.5
X_n = 30
X_col = ['cornflowerblue', 'gray']
X = np.zeros(X_n)
T = np.zeros(X_n, dtype=np.uint8) # Target
Dist_s = [0.4, 0.8] # 분포 시작 지점
Dist_w = [0.8, 1.6]
Pi = 0.5
for n in range(X_n):
wk = np.random.rand()
T[n] = 0 * (wk < Pi) + 1 * (wk >= Pi)
# (A) 암컷이 될 확률 Pi = 0.5로 하여, 무작위로 결정.
# wk < Pi 이면, 0*1 +1 * 0 = 0, wk >= Pi 이면, 0 * 0 + 1 * 1 = 1
X[n] = np.random.rand() * Dist_w[T[n]] + Dist_s[T[n]]
#(B) 질량은 암컷이라면 0.4 ~ 1.2, 수컷이라면 0.8 ~ 2.4의 균일한 분포에서 질량을 샘플링
print('X: '+ str(np.round(X,2)))
print('T: '+ str(np.round(T)))Feature x = [1.94 1.67 0.92 1.11 1.41 1.65 2.28 0.47 1.07 2.19 2.08 1.02 0.91 1.16 1.46 1.02 0.85 0.89 1.79 1.89 0.75 0.9 1.87 0.5 0.69 1.5 0.96 0.53 1.21 0.6 ]
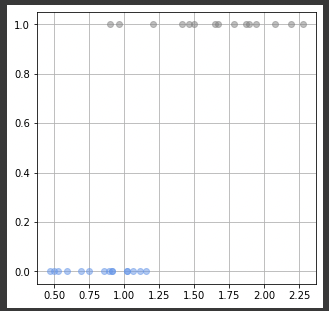
Target Value T = [1 1 0 0 1 1 1 0 0 1 1 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 0 1 0]그래프로 독립변수 x(곤충의 무게)에 대한 종속변수 T (성별)을 출력해보면, 다음과 같이 0 또는 1의 함수값을 가지는 그래프가 보인다.
해당 데이터에서, 일반 회귀 모델을 가상으로 적용 (ax+b)를 적용했을때 T = 0.5 절편을 지나는 직선 모델을 아래와 같이 정의하자. 여기서의 직선 모델은 분류에서 Decision Boundary(결정 경계)라고 한다.
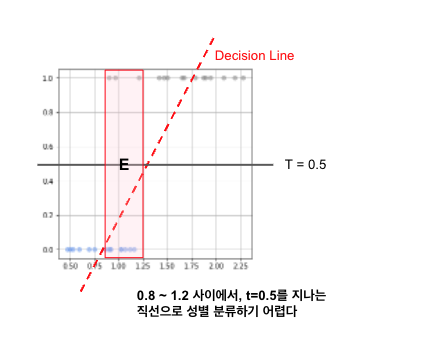
하지만 단순 직선 경계로는, x가 0.8~1.25사이의 구간에서 T를 예측하기가 어렵다. 확률의 개념으로 접근하면 어떨까?
Conditional Probability (조건부 확률)
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred.
출처: https://en.wikipedia.org/wiki/Conditional_probability
조건부 확률(Conditional Probability)란 어떤 사건이 일어 났을때, 다른 한 사건이 일어날 확률의 측도를 뜻한다.
"사건 B가 주어졌을때 A의 조건부 확률" 또는 "B라는 사건에서 확률 A"라고 하며, 간단하게 표현하면, P(A|B) 라고 명칭한다.
이를 원문에서는, P(A|B):
"The Conditional Probability of A given B"
"The probability of A under the condition B"
교재에서는 수컷의 질량 분포가 일 경우, x가 주어졌을때, 수컷일 확률 를 1/3의 조건부 확률로 알아낼 수 있다.
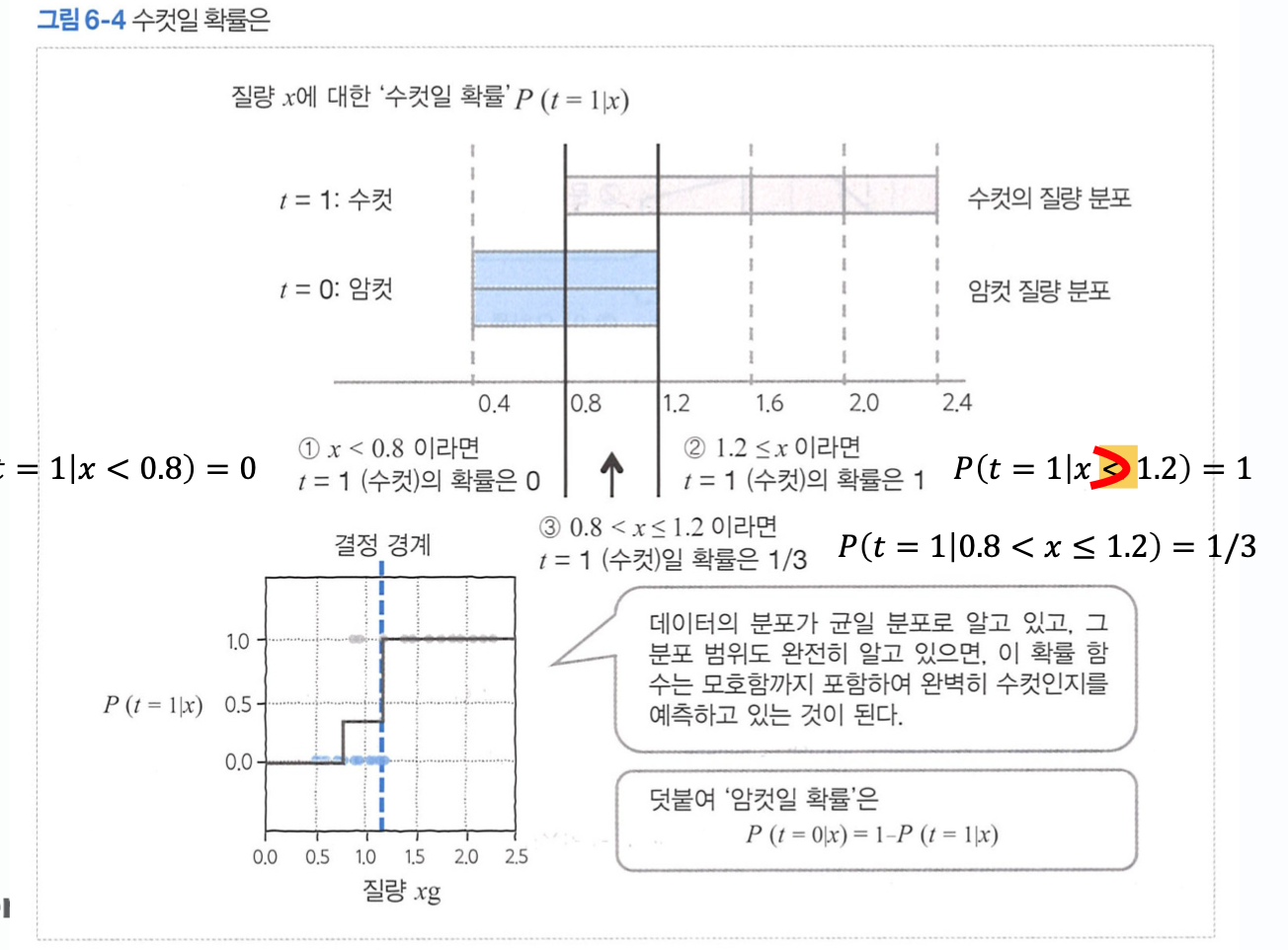
이러한 조건부 확률을 활용하여, 최대 우도법을 이해하고자 한다.
Maximum Likelihood Method (최대 우도법)
통계에 대한 경험이 없기에, 최대 우도법을 이해하느라 고생을 많이 했다. (참고: 사실 아무것도 모른다 ㅠㅠ)
Likelihood (우도) 란, 어떤 결과가 나왔을때 세울수 있는 가설에 대한 평가 측도이다. 가설마다 계산된 우도값 (우도 함수값)을 최대 우도라고 한다. 최대 우도의 원리는, 일어날 가능성이 가장 큰 원인에서 비롯된다고한다.
아래는 최대 우도 추정법을 사용하여 어떤 사건을 예측하는 문제이다.
Q. 어떤 꾸러미에 구슬이 총 100개가 있다. 구슬을 총 10개를 뽑았을때, 검은색 구슬이 4개 흰색 구슬이 6개가 나왔을때 꾸러미안에 검은구슬의 개수를 최대 우도법으로 구해보자.
-
꾸러미의 검은색 구슬 확률:
-
검은 구슬(b)을 뽑을 확률
여기서 E1은 임의의 사건이다. 원래라면, 모든 사건 E에 대해 다뤄야 하지만, 나중에 미분으로 인해 제거 가능함으로 E1 = E 라고 하자. -
어떤 구슬이 나올 확률은 서로 독립적인 사건이며, E1이 일어날 확률은, 개별 사건의 확률의 곱으로 나타낸다.
-
확률 P(E|p)를 최대화 하는것이 최대 우도법이다.
로그는 단조 증가 함수 이기때문에, 최대로 만드는 p를 구하기 위해서 양변에 로그를 취한다. -
최대 우도가 되기 위해서는, 양변에 미분을 하여 0이되는 값을 구한다.
- 검은 구슬의 수 = 100 * p = 40개
즉 정리하면, 꾸러미 안의 검은 구슬은 최대 우도법으로, 40개의 가설이 가장 논리적으로 우도가 높다라는 것이다.
로지스틱 회귀 모델
로지스틱 회귀 모델은 직선 모델과 시그모이드 함수가 결합된 회귀 모델이다. 이름이 회귀이지만, 분류문제에 사용된다.
- 시그모이드 함수:
- 직선 모델:
- 로지스틱:
임의의 가중치 w를 사용하여, 로지스틱 회귀 모델을 구현해보자.
Decision Boundary i 는 y의 중앙을 경계로 하자. (index = 50).
Decision Boudary를 기준으로, 암컷 / 수컷을 나누기 위해 무게 x는 xb[49]와 xb[50]의 평균인B로 지정 (B = 1.25)했다.
# 로지스틱 회귀 모델
def logistic(x, w):
y = 1 / (1 + np.exp(-(w[0] * x + w[1]))) # 시그모이드 함수와 직선모델의 결합
return y
def show_logistic(w):
xb = np.linspace(X_min, X_max, 100)
y = logistic(xb, w)
plt.plot(xb, y, color = 'gray', linewidth = 4)
# Decision Boundary
i = np.min(np.where(y > 0.5))
print(i)
# np.where -> y > 0.5 를 만족하는 y의 인덱스를 반환
B = (xb[i-1] + xb[i]) / 2
# y가 0.5를 넘는 xb[i]와 [i-1]의 평균이 결정 경계의 근사치로 B에 저장
plt.plot([B,B], [-.5, 1.5], color = 'k', linestyle = "--")
plt.grid(True)
return B
W = [8, -10]
fig = plt.figure(figsize = (5,5))
show_logistic(W)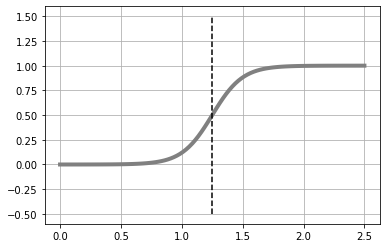
이렇게 로지스틱 회귀 모델에서 Decision Boundary를 구현해보았다, 다음은 최대 우도법과 평균 교차 엔트로피 오차를 사용하여, 로지스틱 회귀모델을 구현하자.
