
푸념: 6시간 동안 작성한 임시 글이 초기화되었다. 아마 PC 2개를 바꿔가며 작성하다가, 다른 PC에서 작업하던 중, 마지막에 작성한 글보다 한시점 앞선 내용으로 자동으로 백업된 것 같다.
방대한 양을 한번에 작업 후, 내용을 복기 하려했는데 이미 금붕어 같은 내 머리로는 기억속에서 80%는 삭제되었다. 야호 :)

앞으로 임시저장 기능(또는 나를)을 완벽히 신뢰 하지않고, velog-backup을 가져와서 백업해둬야 할 것 같다. 다만, 임시저장 기능도 백업 폴더에 저장할 수 있는지 테스트가 필요하다.
정보: velog-backup을 통해, Markdown 형식으로 저장하는것으로 보인다. 이후 Gitblog로 이전할 계획이라면, 틈틈히 사용해보는것도 나쁘지않을것 같다.
Keywords
- 머신러닝이란,
- Feature,
- 대표적인 머신러닝 종류 (회귀, 분류)
- 다차원
- 차원의 저주 - 특징 공간 (Feature Space)
- 선형 분리 불가능(Linearly non-separable) - 매니폴드 (Manifold)
- 머신러닝의 학습 과정
- 목적함수 (중요)
- 머신 러닝의 종류: 지도학습, 비지도 학습
Machine Learning
Feature
학습 및 예측을 할 데이터의 특징을 의미. (Attribute와 동의어)
In machine learning and pattern recognition, a feature is an individual measurable property or characteristic of a phenomenon.[1] Choosing informative, discriminating and independent features is a crucial element of effective algorithms in pattern recognition, classification and regression.
Feature란 어떤 현상이 가지는 고유의 특성 및 속성을 의미한다. Regression 및 Classification에서 분석에 사용할 수 있는 고유한 Feature를 추출해야한다.
Feature Vector
Feature Vector는 객체의 Feature가 가지는 N-차원 벡터로 이루어진, Numerical Information 이다.
머신러닝의 대부분 알고리즘들은 통계 및 분석을 위해 Numerical Information을 사용한다. 예를들어, 임의의 이미지는 Pixel데이터를 지니며 해당 Pixel이 가지는 Numerical Information을 N-차원 벡터로 나타낼수 있다.
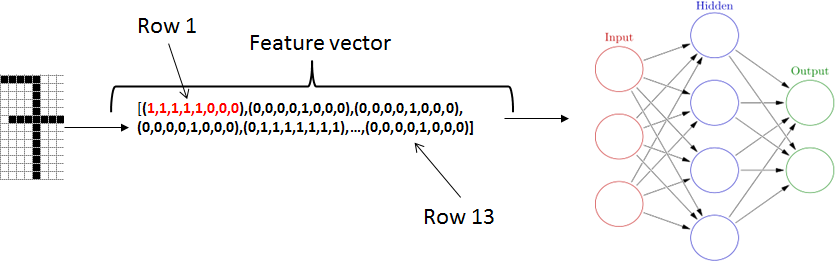
Feature Vector는 선형 예측 함수에서 사용하기 위해, Weight와 Dot Product(내적)하여 종종 사용한다.
Feature Space
주어진 데이터의 Feature Set이다. (Feature Vector로 이루어진 공간). 넓게 표현하여, Real Space(실수 공간)으로 해석할 수 있다.
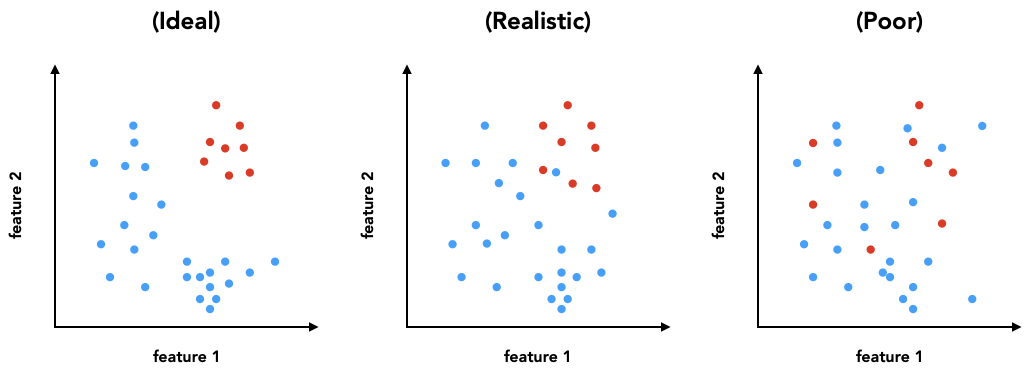
머신러닝의 종류
Regression(회귀)
Regression is a technique for investigating the relationship between independent variables or features and a dependent variable or outcome.
Regression은 Classification과 함께 대표적으로 사용되는 Supervised Learning 테크닉이다. Independent Variable 과 Dependent Variable 사이의 관계를 분석하여, Target Value를 예측한다.
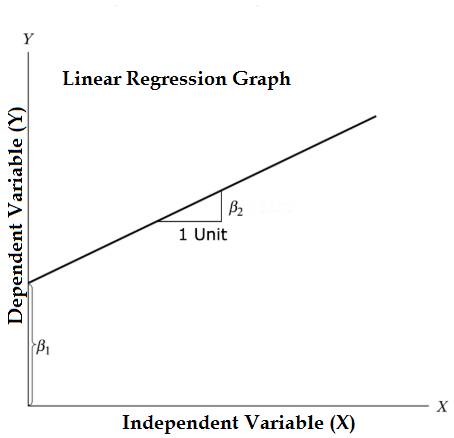
Target Value (예측값)이 실수인 경우.
e.g, 이동하는 물체가 있을 경우, 임의이 시간에 따른 물체의 위치는?

Simple Linear Regression
(ax+b와 같은 직선의 방정식)
Multiple Linear Regression
여러개의 Independent Variable을 가지는 모델이다. Simple Linear Regression에 비해 더 나은 성능을 가진다.
아래와 같이, 하나의 Dependent Variable에 대한 다수의 Independent Variable 함수로 표현할 수 있다.

Logistic Regression
Target Value (예측값)이 실수인 경우.
e.g, 이동하는 물체가 있을 경우, 임의이 시간에 따른 물체의 위치는?
