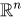
Keywords
- D-dimensional Linear Regression Model
- Linear Combination
- Basis Function
- Gaussian Basis
- Loss Function with Gaussian (Utilizing MSE)
- Analytical Solution with Gaussian (Code)
Note
Analytical vs Numerical Solution
Analytical Solution (해석해) - 정확한 해를 구함
Numerical Solution (수치해) - 근사치를 구함.
N-dimensional Linear Regression Model
입력 데이터와 출력 데이터가 선형관계일때 Linear Regression의 기본적인 선형함수는 다음과 같다.
(1)
하지만, 임의의 입력 데이터가 출력 데이터에 대해, 항상 선형적인 관계를 지닌다고 가정할 수 없다.
이때, X를 어떤 단계를 거쳐 비선형 데이터를 조작할 수 있는데 이를 Basis Function이라고 부른다.
Basis Function
Basis Function을 Wiki 문서에서 찾아보면,
In mathematics, a basis function is an element of a particular basis for a function space. Every function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis vectors.
출처: https://en.wikipedia.org/wiki/Basis_function
Basis Function이란, 함수 공간을 구성하는 기본 원소이며, 임의의 연속함수 ( Function Space)는 Basis Function의 선형 결합으로 표현할수 있다. * Basis Vector의 선형 결합으로 공간을 Span하는 Vector Space의 개념과 유사하다.
이를 확장해서, 우리가 구하려는 함수 값 와 Basis Function인 가 함수공간 을 생성한다면, 입력 데이터 x를 Basis Function 의 선형 결합으로 를 표현할 수 있다는 뜻이 된다.
이를 (1) 식에 적용 시키면,
(2)
(3)
만약, = 1 라는 더미 함수를 사용하게 되면 (3)을 간단하게 표현할 수 있다.
(4)
주목할 점은, (1) 식이 가지는 D != N의 특징 벡터를 다루는 함수식의 개수가 다르다. 데이터의 차원이 기저함수 를 로 Transformation이 있었다는것을 의미하는 것 같다. 아래 설명에 따르면, Basis Function 는 입력 벡터 를 실수공간 차원으로 확장하고, 함수값 y가 가중치 와 에 대해 Linear 한것을 보여준다.
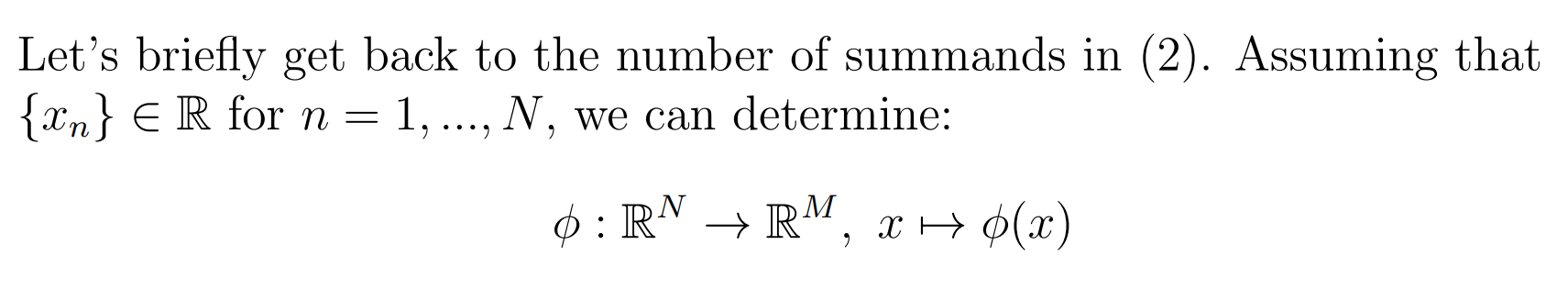
출처: Linear.Models.for.Regression_Handout_Nadia.pdf
Gaussian Basis Function
Basis Function의 종류로 Gaussian Basis Function을 알아보자.
The graph of a Gaussian is a characteristic symmetric "bell curve" shape
출처: https://en.wikipedia.org/wiki/Gaussian_function
Gaussian Function은 함수의 중심을 기준으로 Symmetric (대칭)한 특성으로 그래프가 Bell Curve 형태를 가진다.
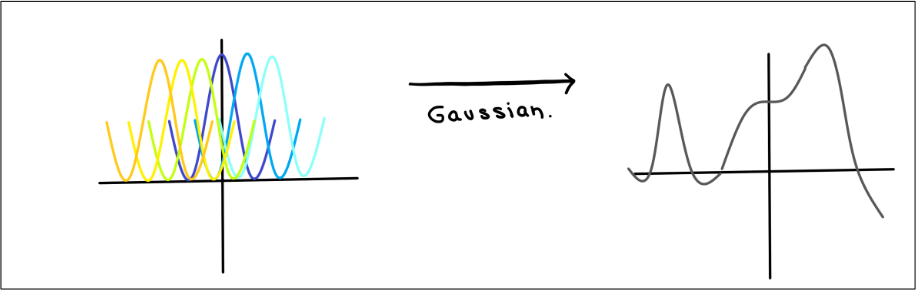
출처: Linear.Models.for.Regression_Handout_Nadia.pdf
Gaussian Basis Function 의 그래프는, 평균(Mean)을 의미하는 와 Standard Deviation을 의미하는 에 의해 결정되며 다음과 같은 함수식을 나타낸다.
- : Height of Graph
- : Index
- : Mean (평균, 함수의 중심을 나타냄)
- : Standard Deviation (표준편차)
- : Variance (분산).
Gaussian Basis Function을 간단히 코드로 구현해보자
# 가우스 기저 함수 구현하기
from IPython.core.pylabtools import figsize
plt.figure(figsize = (5,5))
plt.grid(True)
input_data = np.linspace(0,11, 100)
center = np.mean(input_data)
standard_dev =
a = 2 # Determines the height of graph
print(center) # This is the only point what I would like to give different color
gauss_function = a * np.exp(-((input_data-center)**2)/standard_dev**2)
plt.plot(input_data, gauss_function)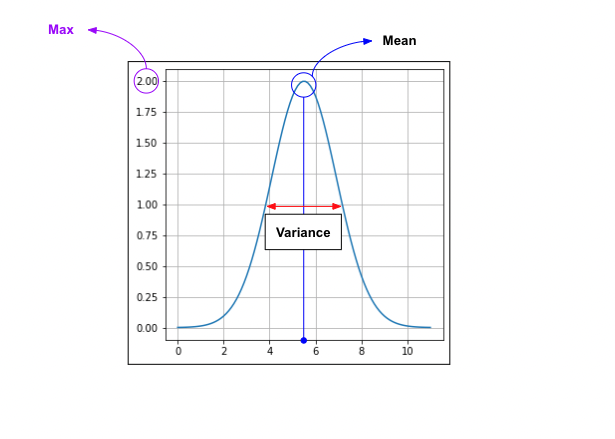
Gaussian Basis Function 그래프를, 여러개 그리는 코드는 다음과 같다.
def gauss(x, mu, s):
return np.exp(-(x-mu)**2 / (2*s**2))
# 4개의 가우스 함수 그리기
M = 4 # 가우스 함수 개수
plt.figure(figsize = (5,5))
mu = np.linspace(5,30, M) # 평균 >> 이게 왜 평균이 되지..?
print(mu)
print(mu.shape)
# print(mu)
s = mu[1] - mu[0] # 인접한 가우스 함수 간 중심 사이의 거리
print("Standard Deviation: {}".format(s)) # 가우스 함수간 거리는 8.333333
xb = np.linspace(x_min,x_max, 40) # ndarray로 100개의 value 저장
print(type(xb)) # return type - numply.ndarray
for j in range(M): # 4번 반복
y = gauss(xb, mu[j], s) #
print(y)
plt.plot(xb, y, color='gray', linewidth=3)
print(y.shape)
plt.grid(True)
plt.xlim(x_min, x_max)
plt.ylim(0, 1.2)아래 이미지에서, 인접한 가우스 함수간 거리 (S)는 8.333 으로, 해당 간격 만큼 가우스 함수 그래프가 그려진것을 확인할 수 있다.
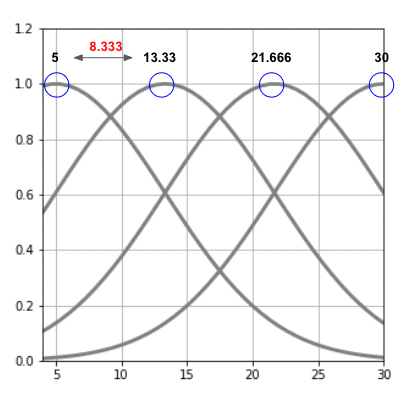
사실, 가우스함수를 이해하기에는 통계에 대한 기본기가 많이 부족하다.
정규 분포, 분산, 표준편차등 기본적인 통계에 대한 공부를 해야할 필요가 느껴진다. 시간이 된다면, 기본기를 복습 후 다시한번 Gaussian Function을 리뷰하도록 해야겠다.
이후 포스팅은, Gradient Descent 모델로 구현했던 나이 - 키 예측모델을 가우스 기저함수인 가우스함수를 사용하여 모델로 구현해보는 코드를 리뷰 하겠다. 그럼 20000 !
