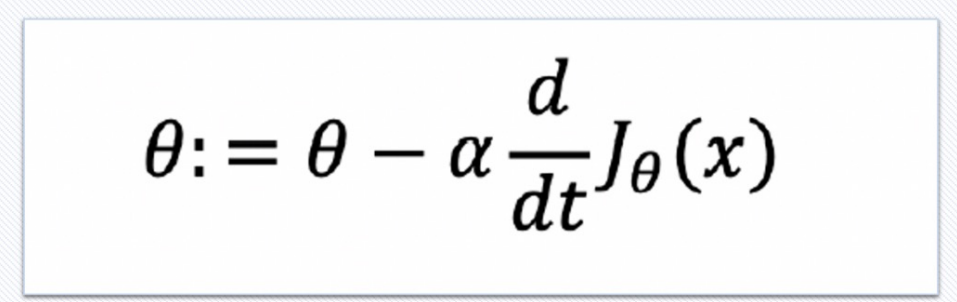[ML] Cost Function

1. Cost Function

1) 직선상에 있지 않은 세 점을 직선으로 표현

• 예제 난이도를 위해 직선은 원점을 지난다고 가정
• 세 점이 $x_1 = (2,1), x_2 = (3,5), x_3 = (5,6)$, 직선으로만 표현한다면 그나마 각 점(데이터)과 직선사이의 에러가 제일 작도록 설정
  

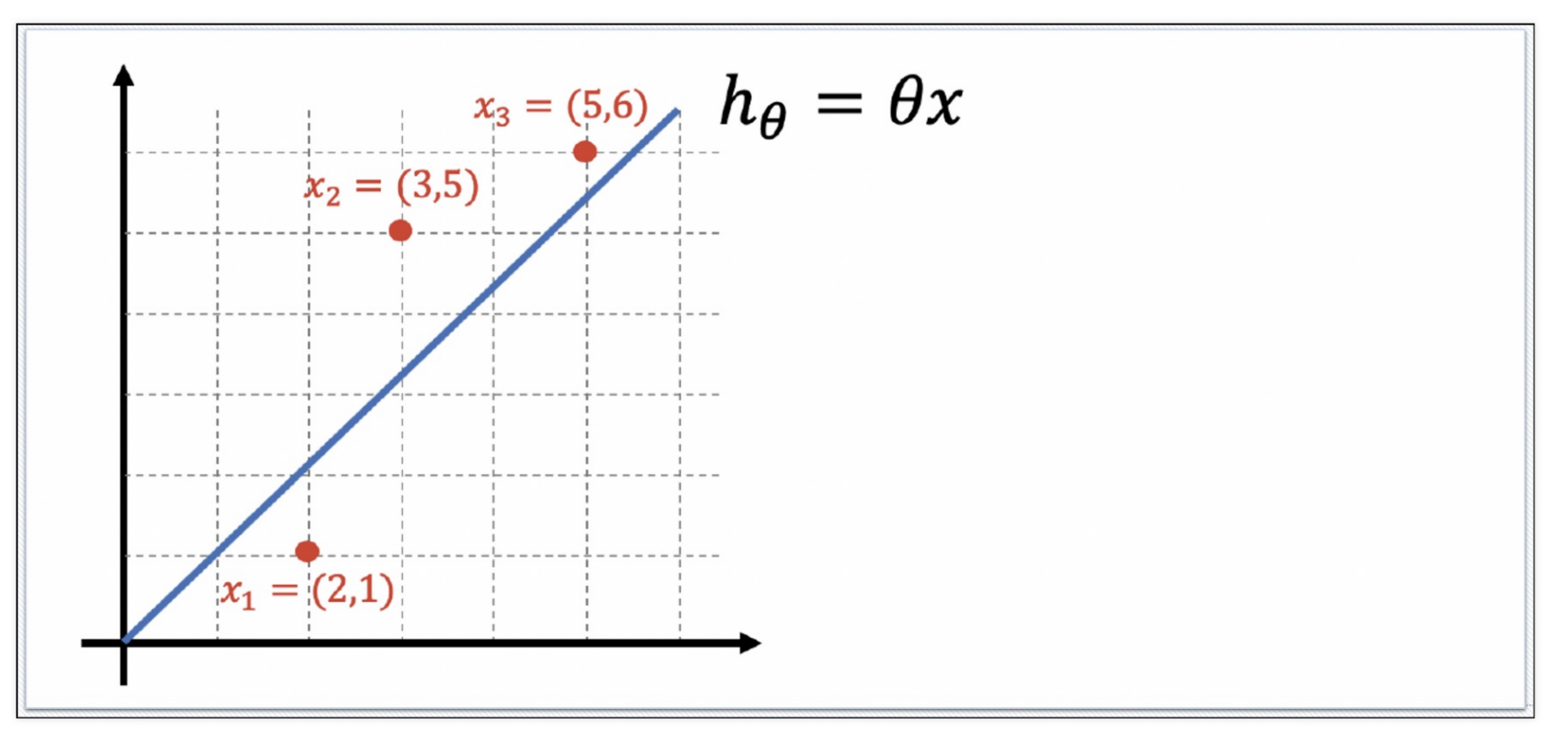
(1) 각각의 에러를 구하고

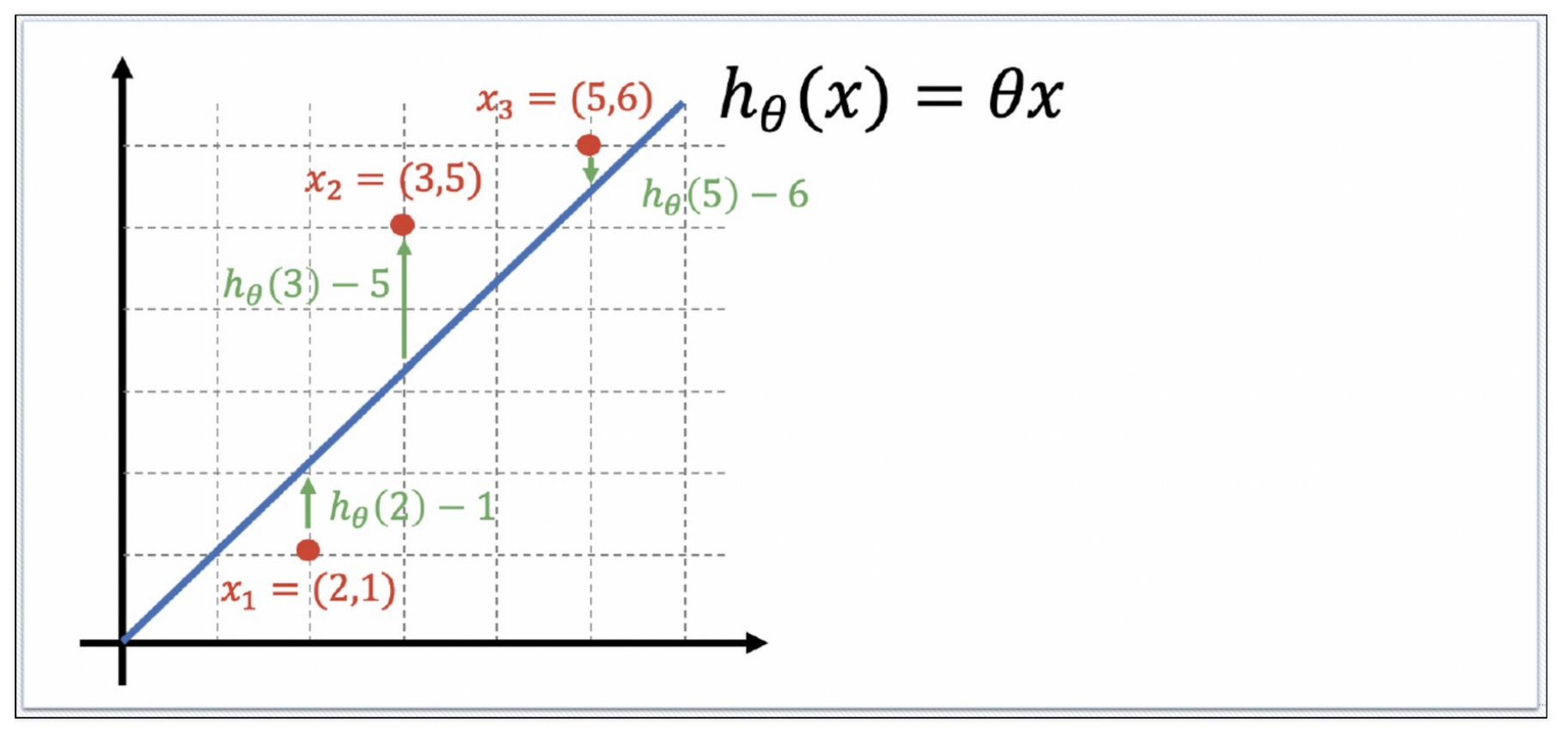
(2) 각각의 에러를 제곱하고 평균값을 구한다

• 에러를 제곱하는 이유는 부호를 없애기 위함, 절대값을 사용하는 경우도 있다
  

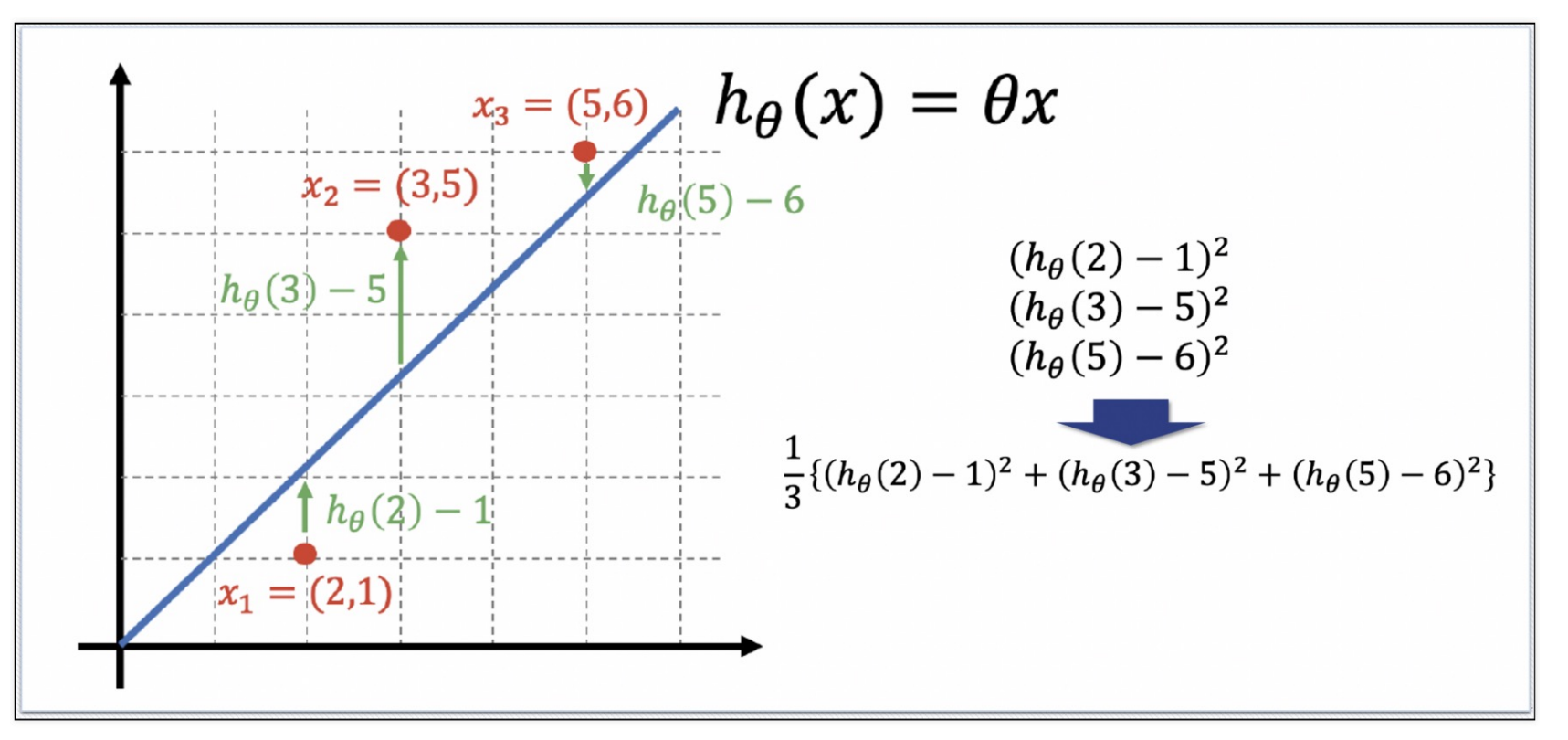
  -> Cost Function
  

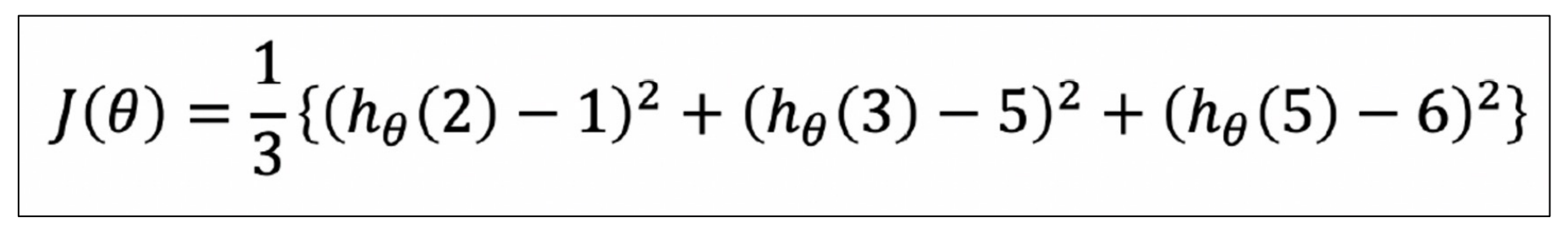
• Cost Fnc을 최소화할 수 있다면 최적의 직선을 찾을 수 있다
  

2) 파이썬으로 Cost Function 최소값 구하기

import sympy as sym

theta = sym.Symbol('theta')

diff_th = sym.diff(38*(theta**2) -94*theta + 62, theta) # 미분
diff_th

# 76𝜃−94 => 𝜃 = 94/76 =1.24

• 그러나 실제는 데이터는 너무 복잡해서 손으로 풀기 어렵다
• Cost Function의 최솟값을 찾기 위해서 대책이 필요

2. Gradient Descent

• 랜덤하게 임의의 점 선택
• 임의의 점에서 미분(or 편미분)값을 계산해서 업데이트
• Learning Rate (학습률) : Gradient Descent에서 alpha는 얼마만큼 theta를 갱신할 것인지를 설정하는 값