계기
머신러닝은 다양하게 접해보았다. 빅분기 준비 , BDA학회, Kaggle등으로 여러 경로로 접해보았지만 아직도 혼동되는 개념들이 많다. 따라서 메타코드 강의를 계기로 혼동되어있는 개념을 다시 잡고 가려고 한다. 강의는 이론 및 실습으로 구성되어 있고 가장 기본이 되는 회귀 부터 포스팅 하겠다. 헷갈리거나 몰랐던 내용 위주로 작성해볼 예정이다.
회귀란 ?
입력값 : 연속값(실수형), 이산값(범주형) , 출력값 : 연속값(실수형)인 형태이다. 즉 특정 변수(피처)들로 타겟(라벨)을 예측을 하는것이다. 피처와 라벨은 독립 변수 , 종속 변수로도 불린다.
종류는 크게 두개로 나뉜다.

선형 회귀
선형회귀는 총 3가지로 나뉜다.
1. 단순 선형 회귀
피처의 종류가 한 개인 데이터데 대한 회귀모델
2. 다중 선형 회귀
피처의 종류가 여러 개인 데이터에 대한 회귀 모델
3. 다항 회귀
독립 변수(피처)의 차수를 높인 회귀 모델
*주의 : 이차원상에 x제곱을 표현하려고 하다보니 그래프 모양이 비선형 형태로 그려지는데 엄밀히 따지면 선형이다.
시그모이드 vs 소프트 맥스

Optimization
평균 제곱 오차 (mean squared error, MSE)
• 회귀 문제에서의 대표적인 손실 함수
• 오차의 제곱의 평균
최소 제곱법 (least square method)
• 최적의 파라미터를 구할 수 있는 한 방법으로, 데이터에 대한 오차를 최소화하도록 함
학습률 (learning rate)
• 계산한 미분값을 그대로 사용해 업데이트 하지않고, 학습률 x 미분값을 사용함
• 학습률이 크면?
• 학습률이 작으면?
경사 하강법 (gradient descent)**
• 손실 함수의 값을 최소화시키는 방향으로 파라미터를 업데이트 한다.
• 손실 함수에 대한 미분값이 0이 되는 방향으로 파라미터의 업데이트 방향을 결정한다.
확률적 경사 하강법 (stochastic gradient descent)
• 데이터가 굉장히 많을 때, 전체 데이터셋을 활용한 경사 하강법은 계산 비용이 매우 큼 따라서 1개의 데이터만으로 업데이트하고, 이를 n번 반복
미니 배치 확률적 경사 하강법 (mini batch stochastic gradient descent)
배치의 크기를 조절해, 학습 속도와 정확도를 조절
이 밖의 다양한 경사 하강법 방법
1. Momentum
2. Nesterov Accelerated Gradient
3. Adagrad (Adaptive Gradient) : 변수마다 업데이트 크기를 조절하는 방식
4. RMSProp
5. Adam
Bias & Variance
편향과 분산은 알고리즘이 가지고 있는 에러의 종류이며 분산은 over-fitting과 관련 있는 개념
,편향은 under-fitting과 관련 있는 개념이다.
1.검증 데이터셋 활용

2.cross validation
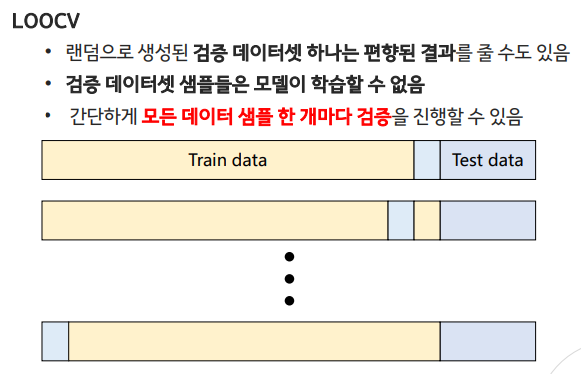
Leave-One-Out Cross-Validation(LOOCV)
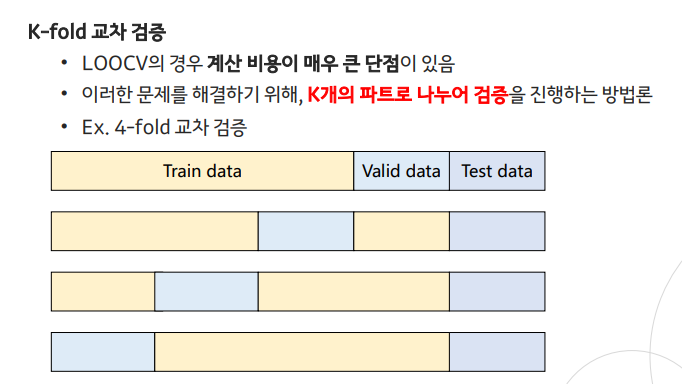
K-fold cross validation
3. 정규화 손실 함수(Regularization)
모델의 복잡도가 커지면 모델의 파라미터 수가 많아지니까 필요없는 파라미터 값을 0으로 만드는방법이다. 즉 람다로 규제를 주는 방법이다
Ridge Regression

Lasso Regression

Bias는 모델이 실제 데이터의 복잡성을 잘 파악하지 못할 때 발생하는데 람다가 커지게 되면 규제가 강화되고 Bias에러값은 늘어난다.
Variance은 모델이 훈련 데이터에 지나치게 민감하게 반응하여 새로운 데이터에 대한 일반화 성능이 낮아지는 것을 나타낸다. 따라서 람다가 커지면 모델의 복잡성이 감소하고, 새로운 데이터에 대한 일반화 성능이 향상되고, 분산 에러가 감소한다.
람다를 적절히 조절하면 편향과 분산 사이의 트레이드오프를 달성할 수 있다. 작은 람다는 모델을 더 복잡하게 만들어 훈련 데이터에 더 적합하게 만들 수 있지만, 과적합의 위험이 있다. 반대로, 큰 람다는 모델을 더 단순하게 만들어 일반화 성능을 향상시킬 수 있지만, 훈련 데이터에 대한 적합성이 감소할 수 있다.
후기
이번 포스팅은 머신러닝에 기본인 회귀에 대해 다뤄보았다. 오랜만에 기본으로 돌아가서 개념을 다뤄보니 내가 미숙했던 부분들이 뭐였는지도 알 수 있었다. 앞으로도 메타코드 강의를 통해 적극적으로 머신러닝 기초부터 다뤄볼 예정이다.
- 메타코드 공식 사이트 : https://mcode.co.kr/
- 강의 유튜브 링크 : https://youtu.be/oyzIT1g1Z3U?feature=shared
#메타코드 #메타코드M #머신러닝 #데이터분석 #회귀 #기초 #이론 #데이터
