SVD(Singular Value Decomposition) - 특이값 분해

Abstract
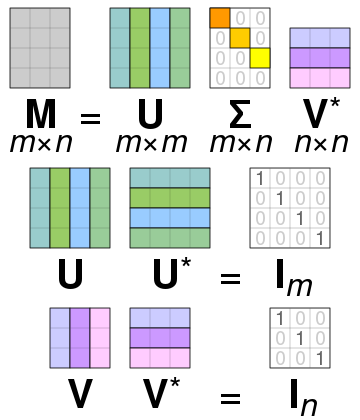
PCA의 경우 정방행렬만을 고유벡터로 분해할 수 있지만, SVD는 정방행렬 뿐만 아니라 행과 열의 크기가 다른 행렬에도 적용할 수 있다. 일반적으로 SVD는 특이값 분해로 불리며, m x n 크기의 행렬 A를 특이 벡터(singular vector)로 이루어진 행렬 U와 V, 대각 행렬 ∑로 분해된다. 수식으로 표현하면 아래와 같이 표현된다.
모든 특이 벡터는 서로 직교(orthogonal)하는 성질을 가지며, 대각 행렬 ∑의 대각 성분이 행렬 A의 특이값이다.
일반적으로 ∑는 m x n의 크기를 가지기 때문에 ∑의 비대각 부분과 대각 원소중 특이값이 0인 부분도 모두 제거해주며 제거한 부분에 대응되는 U와 V의 원소도 같이 제거하여 차원을 줄인 상태로 SVD를 적용한다. 이렇게 간단한 형태로 SVD를 적용하면 A의 차원이 m x n일때, U의 차원을 m x p, ∑의 차원을 p x p, V의 차원을 n x p로 분해하게 된다. 이렇게 분해하는 방법을 Truncated SVD라고 한다.
1. SVD의 활용
- SVD를 이용하면 이미지의 차원 축소를 할 수 있다.
- 이번 실습은 파이썬 구현 코드를 통해 SVD를 이용하여 어떻게 이미지 압축을 하는 지 살펴보겠다.
1-1. 데이터 로드(Dataset - Cifar10)
📌 파이썬 구현코드
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib.image as image
from keras.datasets import cifar10
((x_train, y_train), (x_test, y_test)) = cifar10.load_data()
N, row, col, c = x_train.shape
print(N, row, col, c)데이터 셋은 간단하게 keras의 cifar10을 활용하였고
x_train의 이미지 만을 활용해서 SVD를 확인해보겠다.
아래 print의 결과는 50000(N) 32(row) 32(col) 3(c)이 되겠다.
1-2. SVD 적용
📌 파이썬 구현코드
X = x_train.reshape(N, row*col*c)
X = X.T
C = np.cov(X)
U,s,V = np.linalg.svd(C) # U(3072, 3072), s(3072,) V(3072, 3072)
S = np.diag(s)
V = V.Tx_train 데이터를 행렬로 변환하기 위해 reshape을 적용 (50000, 3072)
C는 covariance matrix를 구하기 위해 numpy의 cov 메소드를 사용 (3072, 3072)
np.linalg의 svd를 통해 U, s, V로 도출되게 된다.
1-3. 차원 축소
📌 파이썬 구현코드
D_reduce = 500
X2Z = U[:,0:D_reduce] # D x D_reduce, projection (3072, 100)
Z2X = U[:,0:D_reduce].T # D_reduce x D, reconstruction (100, 3072)
Z = X.T.dot(X2Z) # (N x D) dot (D x D_reduce) (50000, 100)
X_reconst = Z.dot(Z2X) # (N x D_reduce) dot (D_reduce x D) (50000, 3072)다음은 D_reduce를 100으로 하여 100개의 차원으로 reconstruct를 진행해보았다.
1-4. 시각화
📌 파이썬 구현코드
n = np.random.randint(0,N,5)
plt.figure(figsize = (16,7))
for i in range(5):
img = X_reconst[n[i],:]
img = img.astype(int)
img[img < 0] = 0
img[img > 255] = 255
plt.subplot(2,5,i + 1)
plt.imshow(X[:,n[i]].reshape(row,col,c))
plt.tight_layout()
plt.subplot(2,5,i + 6)
plt.imshow(img.reshape(row,col,c))
plt.tight_layout()
plt.savefig('PCA.eps')

위의 사진은 원본이고 아래는 SVD를 활용하여 차원 축소한 이미지이다.
100개의 차원으로 했을때 이미지가 표현력이 떨어지지만
아래와 같은 코드를 통해 Singular Value를 시각화를 할 수 있다.
plt.plot(np.cumsum(s)/np.sum(s))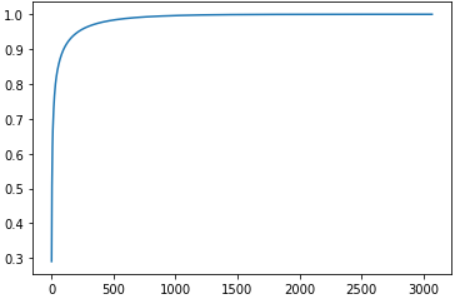
실습에서 사용한 데이터를 적용했다면 Singular Value는 3072개가 나왔을텐데 1번부터 3072번까지 Singular Value를 누적을 해서 더한 값이다.
위의 그래프를 보면 500개의 차원으로 reconstruct시에는 전체 Singular Value의 100프로로 표현이 가능하다. 아래는 D_reduce를 500으로 했을 때의 결과이다.

원본 이미지와의 차이는 크게 나지 않음을 보인다.
Conclusion
이미지 차원 축소는 중요한 정보와 패턴을 유지하면서 이미지의 차원(특징) 수를 줄이는 데 사용되는 기술이다. 이 프로세스는 컴퓨터 비전, 이미지 처리 및 기계 학습과 같은 다양한 영역에서 유용할 것으로 생각되고 실습에서는 SVD를 사용해서 이미지 압축을 해보았다. 이미지 차원 축소의 주요 결과 및 용도는 다음과 같이 생각해 볼 수 있겠다.
- 계산 복잡성 감소: 이미지에는 종종 고차원 특징 공간이 있어 처리 비용이 많이 들 수 있기에, 차원 축소는 데이터 크기를 줄여 처리 속도를 높이고 메모리 요구 사항을 줄임.
- 특징 추출: 차원 축소 기술은 이미지에서 의미 있는 특징을 추출할 수 있습니다. 이러한 기능은 추가 분석, 분류 또는 클러스터링 작업에 사용할 수 있으며 이미지 내의 기본 구조와 패턴을 더 잘 이해하는 데 도움.
- 데이터 시각화: 고차원 데이터는 시각화하기 어렵기 때문에, 이미지 크기를 줄임으로써 더 낮은 차원의 공간, 종종 2차원 또는 3차원으로 데이터를 시각화할 수 있게 되어 더 쉽게 해석하고 분석할 수 있다.
- 노이즈 감소: 고차원 데이터에는 분석 또는 분류 성능에 부정적인 영향을 미칠 수 있는 노이즈 또는 관련 없는 기능이 포함될 수 있다. 그래서 차원 축소는 잡음이 있는 기능의 영향을 제거하거나 줄이는 데 도움이 되어 결과를 개선할 수 있다.
- 압축: 이미지 차원 감소 기술, 특히 PCA(Principal Component Analysis) 또는 자동 인코더와 같은 손실 방법을 이미지 압축에 사용할 수 있습니다. 이는 스토리지 또는 대역폭이 제한된 애플리케이션에서 특히 유용할 것임.
- 머신 러닝 알고리즘 가속화: 객체 인식 또는 이미지 분류와 같은 이미지 기반 머신 러닝 작업에서 차원 축소는 교육 시간을 크게 단축하고 전반적인 성능을 향상시킬 수 있음.
- 이미지 클러스터의 시각화: 차원 축소 방법은 유사한 이미지를 저차원 공간에 함께 클러스터링하여 이미지 그룹 또는 클래스를 더 잘 시각적으로 표현할 수 있도록 함.
- 이미지 재구성: 오토인코더와 같은 일부 차원 축소 기술은 축소된 차원 표현에서 원본 이미지를 재구성할 수 있다. 이미지 노이즈 제거 및 인페인팅과 같은 작업에 유용할 것임.
- 전이 학습: 전이 학습 시나리오에서 차원 축소는 사전 훈련된 모델을 차원이 다른 새로운 이미지 데이터 세트에 적용하는 데 도움이 될 것임.
References
