(1) Bayesian linear regression

김민솔·2024년 2월 25일

Bayesian

목록 보기

1/4

해당 내용을 다루기 앞서 베이시안 딥러닝에 빠지게 된 계기부터 소개하고자 합니다. 저는 생성모델 분야에 큰 관심을 가지고 있었고, diffusion 모델을 공부하던 중에 이를 이해하기 위해 주요한 개념이 바로 베이시안이라는 것을 알게 되었습니다. 따라서 PRML 책과 최성준 박사님의 Bayesian Deep Learning 강의 내용을 통해 베이시안 ML 개념을 공부하였고, 앞으로 올리게 될 시리즈는 이를 정리하기 위한 목적으로 작성되었습니다. 추가로 Bayesian learning을 공부하기 위하여 학습한 자료들은 레퍼런스에 기재하였습니다!

Content

Linear regression

베이시안 관점을 선형 회귀 문제에 적용하기 전에, 기본적인 선형 회귀에 대해서 살펴보겠습니다.

선형 회귀의 목표는 주어진 continuous 데이터셋이 존재할 때, 독립 변수 X와 종속 변수 y간의 선형 상관 관계를 모델링하는 것입니다. 즉, 두 변수 간의 관계를 가장 적합하게 표현하는 선형 모델을 찾는 것이며, 이를 만드는 최적의 weight를 학습을 통해 구해야 합니다.

$y = f(\mathbf{x}) + \epsilon = \mathbf{x}^T\mathbf{w} + \epsilon \quad \quad$ $\epsilon$ ~ $\mathcal{N}(0, \sigma^2_n)$
$\mathcal{D} = \{(x_i, y_i)\}^{n}_{i=1}$
$X = [x^T_1, …, x^T_n]^T$

X와 weight w가 주어졌을 때 타겟 값 y에 대한 분포를 표현하는 likelihood를 구하는 식은 다음과 같습니다.

p(\mathbf{y}|X, \mathbf{w}) = \prod^n_{i=1}p(y_i|\mathbf{x}_i,\mathbf{w})\\ \quad \quad \quad \quad \quad \quad \quad \quad\quad\quad\quad\quad =\prod^n_{i=1} \frac 1 {\sqrt{2\pi\sigma^2_n}} exp(- \frac {(y_i - \mathbf{x}^T_iw)^2} {2\sigma^2_n}) \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ \ = \frac 1 {{2\pi\sigma^2_n}^{n/2}} exp(-\frac 1{2\sigma^2_n} ||\mathbf{y}-X^T\mathbf{w}||) \\ \quad\quad\quad\quad\quad \ \ \ = \mathcal{N}(\mathbf{y};X^T\mathbf{w},\sigma^2_nI)

Likelihood를 최대화하는 방법으로 최적의 파라미터를 찾는 방법이 MLE(Maximum Likelihood Estimation)입니다. Log likelihood에 gradient를 적용하여 likelihood를 최대화하는 파라미터를 찾을 수 있습니다. 하지만 앞으로 보게 될 베이시안 회귀에서는 MLE 방법으로 최적화하지 않습니다.

Basic of Bayesian

그런데, 일반 선형 회귀로도 문제 해결이 가능함에도 베이시안 확률론을 도입한 이유는 무엇일까요?

베이시안 확률론이 사용되는 이유에 대해서 우선적으로 짚어보고자 합니다. 베이시안 확률론의 가장 큰 장점은 모델의 불확실성을 측정할 수 있다는 것입니다. 데이터셋의 양이 거대해지면서 이에 대한 불확실성이 증가되었고, 이외에도 정보, 지식 등에서도 불확실성을 가집니다. 이를 베이시안을 통해서 표현할 수 있다면, 모델에 대해서 설명 및 분석이 가능해집니다. 또한 자율주행 분야를 예시로 들면, 하나의 판단이 사고로 이루어질 수 있기 때문에 모델의 불확실성을 측정하는 것이 중요하게 되죠. 그렇다면 이러한 베이시안 관점이 선형 회귀에 적용되는 과정을 살펴보겠습니다.

베이시안을 다룰 때 필수적으로 사용되는 베이즈 이론입니다.

p(\mathbf{w}|\mathcal{D}) = \frac {p(\mathcal{D}|\mathbf{w})p(\mathbf{w})} {p(\mathcal{D})}

파라미터에 대한 분포를 다루는 사전 확률 분포(prior)를 두고, 가능도(likelihood)와 곱한 후에 사후 확률 분포(posterior)를 구해야 합니다. prior를 통해서 모델 학습 전에 갖고 있는 사전 지식을 문제 해결에 적용할 수 있으며, likelihood를 이에 곱해가면서 posterior를 구하게 되는 것입니다.

즉, 데이터 X와 이에 대한 타겟 값 y가 주어졌을 때의 파라미터의 분포인 posterior를 구하는 것이 베이시안 ML의 첫 번째 목표입니다. 이때 posterior를 최대화하는 방향으로 학습을 진행하여 weight w를 구하게 되며, 이러한 방법을 MAP(Maximum A Posterior estimation)라고 부릅니다.

베이시안 ML의 두 번째 목표는 새로운 input이 들어왔을 때 이를 예측하는 predictive distribution을 구하는 것입니다. 위에서 구한 posterior에 target distribution을 곱한 후, 이를 파라미터 w로 적분하여 구하게 됩니다. predictive distribution의 mean은 모델이 새로운 데이터에 대해 내놓은 예측 값으로 사용되며 predictive distribution의 variance는 앞에서 언급한 모델의 불확실성을 표현하는 값으로 사용됩니다.

다음으로는 베이시안 선형 회귀에 대해 알아보겠습니다.

베이시안 선형 회귀를 해석하는 관점으로는 weight space view와 function space view가 있습니다. 각각에 대해 살펴보겠지만, 도출되는 결과는 결국 같습니다.

Weight space view

위에서 설명한 Bayesian formulation으로 구한 posterior 및 MAP, predictive distribution을 구한 식의 전개는 필기한 노트 스캔본으로 올리겠습니다!

여기에 Kernel Trick을 추가하겠습니다. Kernel Trick은 input space에 있는 x를 고차원의 feature space로 매핑하여 linear regression의 정확도를 높이기 위함입니다. 선형 문제로 풀 수 있는 문제에는 한계가 존재하는데, 데이터 x를 고차원으로 이동시켜 선형 모델이 더 좋은 성능을 갖게 하는 방법입니다. (비선형 문제를 선형 모델로 푸는 것도 가능해집니다! svm 모델에서 사용하는 방식입니다.)

Kernel을 적용하여 앞에서 구했던 predictive mean과 predictive variance에 적용하는 과정은 다음과 같습니다.

Function space view

Function space 관점으로 베이시안 선형 회귀 문제를 해결하기 위해서는, conditional expectation과 conditional variance 수식을 알아야 합니다. 증명 과정은 Appendix에 남겨두었습니다.

E(x|y) = E(x) + Σ_{xy}Σ ^{−1}_{yy} (y − E(y))\\ Σ_{x|y} = Σ_{xx} − Σ_{xy}Σ ^{−1} _{yy} Σ_{yx}.

f(x)를 zero-mean Gaussian process로 두고, 이에 대한 predictive function $f(x_*)$ 이 서로 jointly Gaussian을 이룬다고 두겠습니다.

$f(x) = [f(x_1), ... , f(x_n)]^T \in \mathbb{R}^n$
$f(x_*) \in \mathbb{R}^n$
$y = f(x) + \epsilon$
$cov(y(x_1, x_2)) = K(x_1, x_2) + \sigma^2_n$

위에서 정리한 식을 통해 jointly Gaussian을 표현한 후에, 위에서 언급한 conditional expectation과 conditional variance를 사용하면 predictive mean과 predictive variance를 구할 수 있습니다. 수식 전개는 스캔본으로 남기겠습니다.

앞에서 스포를 했듯이, weight space 관점과 function space 관점으로 도출한 결괏값이 동일한 것을 확인할 수 있습니다! (사실 같은 결과를 다른 관점으로 바라본 것이니 당연한 사실입니다)

Appendix

Random variable

확률공간에서 가측공간으로 이동시키는 함수이며, 이는 가측 가능한 확률 공간 및 실수들의 집합으로 만들어진 시그마필드인 Borel measure space에서 정의되었습니다. Random variable는 값이 아니라 함수인 점 또한 짚고 넘어갈 만합니다.

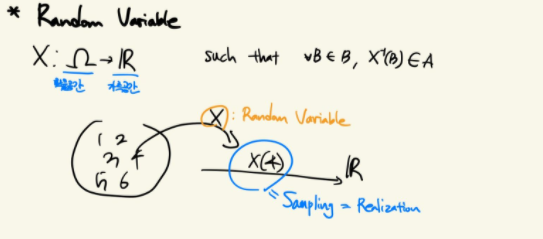
Random process

Random variable이 하나의 값을 뽑는 함수였다면, Random process는 Random variable의 sequence로 볼 수 있습니다. 다르게 해석하면, 하나의 함수를 뽑는 함수로도 가능합니다. 이때 time 개념이 되는 t를 고정하면 Random variable이 됩니다.

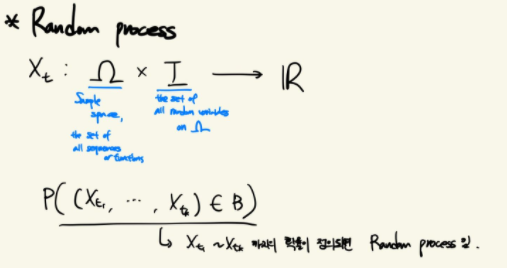
여기에 Stationarity 개념을 적용할 수도 있습니다. tau 만큼의 시퀀스 간격을 가지는 Random process에 대해 서로 같다는 개념입니다.

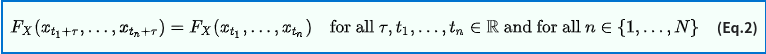
wide-sense stationary를 만족하기 위해서는 다음을 만족해야 합니다.

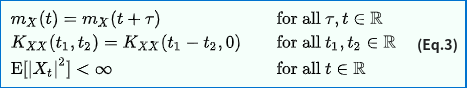
Stationary process에는 다양한 함수를 적용할 수 있으며 예시로는 mean function, acf, acvf 등이 있습니다. 이 중 acvf(auto covariance function)만 식으로 남겨두겠습니다.

C_x(t, s) = \mathbb{E}[X_t-m_x(t)][X_s-m_x(s)]

Stationary process를 GP에 적용할 때의 장점은, mean function이 상수가 된다는 점입니다. 따라서 베이시안 선형 회귀를 다룰 때 가우시안을 zero mean으로 가정할 수 있었던 것입니다!

Gaussian process

한 Random process $X(t)$ 가 있고, 한정된 index set $t_1,…t_k$ 에 대하여 $X(t_1),…X(t_k)$ 가 jointly gaussian을 만족할 경우에 $X(t)$ 를 Gaussian process라고 부르게 됩니다. 표기는 $X(t)$ ~ $GP(m(t), k(t,s))$ 로 이루어집니다.

$m(t)$ : mean function
$k(t, s)$ : covariance function / $k(t, s) = cov(X(t), X(s))$