(2) Bayesian linear classification

김민솔·2024년 2월 26일

bayesian prml

Bayesian

목록 보기

2/4

저번 포스트에서는 베이시안 선형 회귀를 다루면서 기본적인 개념들도 포함하여 소개하는 시간을 가졌습니다. 이번 포스트에서는 베이시안 선형 분류가 어떻게 이루어지는지 알아보겠습니다.

Content

베이시안 분류 문제가 베이시안 회귀보다 어려운 이유는 타겟 자체가 불연속적인 성질을 띄고 있어 적분이 되지 않기 때문입니다. 따라서 Gaussian likelihood를 사용할 수 없게 되죠.

이를 해결하기 위하여 두 가지 방법이 존재하며, 각각 discriminative 방법과 generative 방법입니다.

Discriminative

discriminative 방법은 output을 activation function으로 표현하는 것입니다. 따라서 직접적으로 p(y|x)를 모델링할 수 있게 됩니다. 데이터들로부터 최적의 분류기를 구성하는 Decision theory로 해당 방법을 볼 수 있습니다.

Decision Theory

Decision Theory의 목표는 feature space를 각각의 decision region으로 나누는 최적의 분류기를 구성하는 것입니다.

joint distribution p(x, y)를 통해 데이터 x와 타겟 y의 관계를 표현하고, 이에 Loss function을 곱한 것을 적분하여 Loss 값을 구하는 방법입니다.

R_L(c) = \int L(y, c(x))p(y,x)dydx

MLE

Class가 2개만 있는 binary 문제로 가정한 후, maximum likelihood로 분류 문제를 풀어보겠습니다.

Logistic: $p(C_1|\phi) = \sigma(\mathbf{x}^Tw)$ / $p(C_2|\phi) = 1- p(C_1|\phi)$
Likelihood: $p(t|w) = \prod^N_{n=1}y^{t_n}\{1-y_n\}^{1-t_n}$ $y_n = p(C_1|\phi_n)$ , $t_n \in \{0, 1\}$ , $\phi_n = \phi(x_n)$
Expectation: $E(w) = - \ln p(t|w) = - \sum^N_{n=1}\{t_n \ln y_n + (1-t_n)\ln(1-y_n) \}$
Gradient: $\nabla E(w) = \sum^N_{n=1}(y_n - t_n)\phi_n$

위에서 시그마는 sigmoid 함수를 의미합니다. class가 2개이기 때문에 activation function을 sigmoid로 설정한 것입니다. class가 여러 개일 때는 softmax function을 사용하면 되겠죠? multiclass logistic 문제를 MLE로 푸는 과정은 노트 필기로 남겨두었습니다.

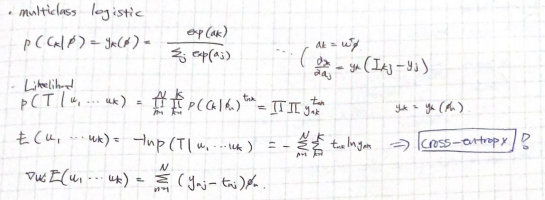
IRLS(Iteratively reweighted least squares)

IRLS는 목적 함수를 이용한 반복적인 학습을 통해서 최적화 문제를 해결하는 방법입니다. 딥러닝에서 weight update하는 방법과 매우 유사합니다.

w^* = w - \mathbf{H}^{-1}\nabla E(w)

$\mathbf{H}$ : Hessian matrix(= $E(w)$ 를 이계도함수로 표현한 행렬)
$\nabla E(w)$ : gradient of a function E(w)

Loss function을 sum of squared error로 설정하였을 때의 IRLS로 최적의 파라미터 w를 구하는 과정을 노트 필기로 남겨두었습니다.

Generative

Generative 방법은 베이즈 이론을 통해서 posterior를 간접적으로 구하는 방법입니다.

marginalize로 p(x)를 구하여 ( $p(x) = \sum_y p(y)p(x|y)$ ) outlier, unlabelled data 등 input 데이터들을 처리하는 것이 용이해집니다. 하지만 discriminative 방법에 비해서 분류 문제 해결에 필요한 비용이 더 많이 들게 됩니다.

Modeling

Class가 2개 이상일 때에 posterior인 generalized linear model을 구하는 과정입니다. (class가 2개일 때는 logit function과 logistic sigmoid function을 통해 posterior를 구할 수 있게 됩니다. 이번 포스트에서는 생략하겠습니다!)

p(C_k|\mathbf{x})= \frac {p(\mathbf{x}|C_k)p(C_k)} {\sum _j p(\mathbf{x}|C_j)p(C_j)}=\frac {\exp(a_k)} {\sum _j \exp(a_j)}

$a = \ln p(\mathbf{x}|C_k)p(C_k)$

class conditional density $p(\mathbf{x}|C_k)$ 와 class prior인 $p(C_k)$ 를 활용하여 posterior를 간접적으로 구할 수 있게 되며, 이때 사용된 normalized exponential 함수를 softmax 함수라고 부릅니다.

MLE

log likelihood function을 general case에 대해 나타내면 다음과 같습니다. 해당 함수를 최대화하는 파라미터를 찾으면, 선형 분류 문제를 해결할 수 있습니다.

\ln p (t_n|{π_k}) = \sum^N_{n=1} \sum^K_{k=1} t_{nk}\{ \ln p(\phi_n|C_k) + \ln π_k\}

$π_k = \frac {N_k} N$ : prior class probabilities
$p(\phi_n|C_k)$ : general class conditional densities
$t_n$ : one-hot encoded 타겟 벡터

Laplace Approximation

이번에는 MAP 최적화 방법으로 베이시안 선형 분류 문제를 해결해보겠습니다.

우리는 위의 과정들을 통해서 likelihood를 얻어낼 수 있습니다. 그렇다면 prior와 likelihood의 곱으로 posterior를 표현할 수 있을까요? 하지만, 여기서 문제가 하나 발생합니다. 베이시안 선형 회귀에서는 prior와 likelihood 모두 가우시안 분포로 두었기 때문에 posterior도 가우시안으로 가정하였습니다. 반면에 베이시안 선형 분류에서는 likelihood가 어떤 분포를 가진다고 특정할 수 없기 때문에 posterior가 가우시안 분포라고 둘 수 없게 됩니다.

따라서 posterior를 근사하여 구하는 방법인 Laplace Approximation을 적용하여 likelihood를 사용하지 않고 posterior에 가까운 가우시안 근사 분포를 구합니다. posterior의 mode를 찾고, 이를 중점으로 하는 가우시안 분포를 생성하는 것으로 가우시안 근사를 생성합니다.

$p(z) = \frac 1 Z {f(z)}$
- $z$ : 하나의 연속적인 변수, $Z$ : normalization factor $\int f(z)dz$
$\ln f(z) \simeq \ln f(z_0) - \frac 1 2 (z-z_0)^TA(z-z_0)$
$f(z) \simeq f(z_0) \exp \{ - \frac 1 2 (z-z_0)^TA(z-z_0) \}$