(4) Variational Inference - [2]

김민솔·2024년 3월 2일

Bayesian

목록 보기

4/4

저번 포스트에서는 Variational Inference가 무엇인지, posterior를 근사하는 방법(ELBO), multi-layer에서 ELBO에 필요한 likelihood를 구하는 방법에 대해서 알아보았습니다. 이번에는 변분 추론이 실제 Neural network에서 실제로 어떻게 활용되었는지를 VAE를 통해 집중적으로 알아보겠습니다.

VAE(Varitaional AutoEncoder)

VAE는 변분 추론을 활용한 generative model 중 좋은 성능을 보였던 대표적인 모델입니다. 이름에서 볼 수 있듯이 AutoEncoder의 모델 구조를 차용하여 Encoder와 Decoder로 이루어져 있습니다. Encoder에선 data 분포를 latent space로 압축하는 과정을 수행하고, Decoder에선 latent space에서 샘플링한 z를 input data x와 비슷하게 만들어내는 과정을 수행합니다.

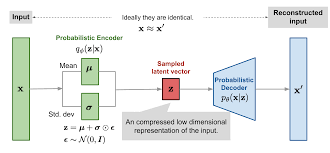
Objective function으로는 ELBO를 활용합니다. 이에 대한 설명은 저번 포스트에 되어 있으니 참고해주시면 감사하겠습니다!

\mathcal{L}(\theta , \phi; x^{(i)}) = -KL(q_\phi(z|x^{(i)})||p_{\theta}(z)) + E_{q_\phi(z|x^{(i)})}[\log{p_{\theta}(x^{(i)}|z)}]

$q_\phi(z|x^{(i)})$ : Variational posterior → Encoder
$p_{\theta}(z)$ : prior
$p_{\theta}(x^{(i)}|z)$ : likelihood → Decoder

목적 함수인 ELBO를 최대화하여 posterior에 근사하는 분포 $q(w)$ 를 학습하는 것이 목표입니다. 즉 ELBO가 최대화되는 파라미터들을 여러 번의 가중치 업데이트를 통해 구합니다.

({\theta}^*, \phi^*) = {argmax}_{{\theta}, \phi}\mathcal{L}(\theta , \phi; x^{(i)})

Reparameterization Trick

Forward과정에서는 샘플링이 문제가 되지 않지만, 모델의 가중치를 업데이트 하기 위해서는 Backprop을 거쳐야 합니다. 이때 샘플링 연산은 미분이 되지 않는다는 문제점이 발생합니다.Reparameterization Trick은 해당 문제를 해결하기 위하여, 미분 가능한 함수를 도입하여 network에서 샘플링이 가능하게 합니다.

기존에는 z가 인코딩된 분포 $p_\phi(z|x)$ 에서 샘플링되었기 때문에 backprop이 불가능하였습니다. z를 직접적으로 샘플링하지 않고, $\epsilon$ 을 std( $\mathcal{N}(0,1)$ )에서 샘플링 한 후에 $z = \mu + \sigma\epsilon$ 과 같이 표현하게 되면 z에 관한 미분이 가능해집니다. 해당 함수로 z를 표현하는 것이 가능한 것을 보여주는 증명은 다음과 같습니다.

E(z) = E(\mu + \sigma\epsilon) \\ \quad \quad \ \ = \mu + \sigma E(\epsilon) \\ = \mu

Var(z) = E(z^2) - (E(z))^2 \\ \quad \quad \quad \quad = E((\mu + \sigma\epsilon)^2) - \mu^2 \\ \quad \quad \ = E((\sigma\epsilon)^2) = \sigma^2

Reparameterization trick을 활용한 목적 함수는 다음과 같습니다.

\mathcal{L}(\theta , \phi; x^{(i)}) = -KL(q_\phi(z|x^{(i)})||p_{}(z)) + \frac 1 L \sum^L_{l=1}\log{p_{\theta}(x^{(i)}|z^{i,l}})

$E_{q_\phi(z|x^{(i)})}[\log{p_{\theta}(x^{(i)}|z)}] = E_{z \sim q_\phi}[f(z)]$
$E_{z \sim q_\phi}[f(z)] = E_{z \sim q_\phi}[f(g_\phi( \epsilon,x^{(i)}) )] \simeq \frac 1 L \sum f(g_\phi( \epsilon,x^{(i)}))$ ← reparameterization trick + Monte carlo integration

VAE를 구현한 코드는 깃허브에 올려 두었으니 참고해보시면 좋을 것 같습니다! 여러 포스트를 거쳐서 Bayesian 확률론과 머신러닝/딥러닝에 어떻게 적용되는지를 알아보았습니다. Bayesian에 관심 있으신 분들에게 도움이 되는 포스트들이 되었으면 좋겠네요:)

Reference

[1] Bayesian Deep Learning, 최성준, https://www.edwith.org/bayesiandeeplearning/joinLectures/14426

[2] Pattern recognition and machine learning, https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf

[3] Auto-Encoding Variational Bayes, https://arxiv.org/pdf/1312.6114.pdf

김민솔

Interested in Vision, Generative, NeRFs

이전 포스트

(4) Variational Inference - [2]

Bayesian

VAE(Varitaional AutoEncoder)

Reparameterization Trick

Reference

(3) Variational Inference - [1]

0개의 댓글