변분 추론(Variational Inference)은 확률 모델의 근사적 추론 방법 중 하나입니다. posterior가 복잡하여 직접적으로 구할 수 없는 경우에, 확률 분포를 근사하는 방법입니다. (실제로 posterior를 직접 계산하는 것은 거의 불가능에 가깝습니다.)
이번 포스트에서는 posterior 근사를 위해 ELBO가 사용되는 이유 및 kernel function의 관점으로 변분 추론이 multi-layer에서 이루어지는 과정을 살펴보고, 다음 포스트에서는 실제로 변분 추론이 어떻게 사용되고 있는지 VAE의 관점에서 다뤄보겠습니다.
ELBO
우리는 posterior p(w∣X,y)를 직접 계산하지 않고, 이에 근사하는 분포인 variational dist. q(w)를 구해야 합니다. 따라서 두 분포의 KL divergence 값을 최소화하는 방향으로 최적화 문제를 접근해보겠습니다.
KL(q(w)∣∣p(w∣X,y))=∫q(w)logp(w∣X,y)q(w)dw
하지만, posterior p(w∣X,y)를 구할 수 없기 때문에 해당 적분 계산이 불가능합니다. 따라서 직접적으로 KL 값을 최소화하지 않고, ELBO(Evidence of Lower Bound)를 도입하여 문제를 해결합니다.
logp(D)=∫q(w)logp(D)dw =∫q(w)logp(w∣D)p(D∣w)p(w)dw =∫q(w)logq(w)p(w∣D)q(w)p(D∣w)p(w)dw=∫q(w)logp(w∣D)q(w)dw+∫q(w)logq(w)p(D∣w)p(w)dw=KL(q(w)∣∣p(w∣X,y))+ELBO
log marginal likelihood logp(D)를 전개하면 다음과 같이 근사 분포와 사후 분포 간의 KL divergence 값과 lower bound의 합으로 나타낼 수 있습니다. 이때 marginal likelihood는 고정이기 때문에, ELBO를 최대화하여 q(w)와 p(w∣X,y) 분포 차를 최소화하는 문제를 해결하는 것이 가능합니다.

그렇다면, ELBO 식을 더 자세히 살펴보겠습니다.
ELBO=∫q(w)logq(w)p(D∣w)p(w)dw =∫q(w)(logp(D∣w)+logq(w)p(w))dw =∫q(w)logp(y∣X,w)dw−KL(q(w)∣∣p(w))
- ∫q(w)logp(y∣X,w)dw: likelihood under q(w) / reconstruction error
- KL(q(w)∣∣p(w)): prior fitting term / regularization parameter
첫 번째 term에서는 근사 분포 q(w)에 대한 기댓값으로, reconstruction error에 해당하게 됩니다. 두 번째 term에서는 근사 분포 q(w)와 prior p(w)의 kl divergence 값이 작아지도록 목적 함수가 설정되어 regularization 역할을 수행합니다.
Variational Inference in multi-layer (with kernel function)
prior fitting term은 근사 분포와 사전 확률 분포가 가까워지도록 학습시킵니다. 따라서 우리가 주목해야 할 term은 q(w)에 대한 likelihood 함수입니다.(regularization term에 대해서 따로 kernel을 도입하지 않아도 되기 때문입니다.) 가능도 함수를 구하기 위해 아래의 kernel function을 도입하겠습니다.
- K(x,y)=∫p(w)p(b)σ(wTx+b)σ(wTy+b)dwdb
- K^(x,y)=K1∑k=1Kσ(wkTx+bk)σ(wkTy+bk) ← Monte carlo Intergration
이때 커널을 K^(X,X)=ΦΦT로 치환하여 single, multi layer에 대한 likelihood를 표현하면 다음과 같이 됩니다.
single layer
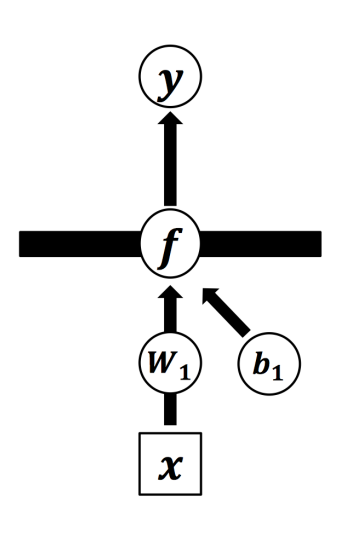
P(Y∣X)=∫N(Y;0,ΦΦT+τ−1)p(w)p(b)dwdb
multi layer
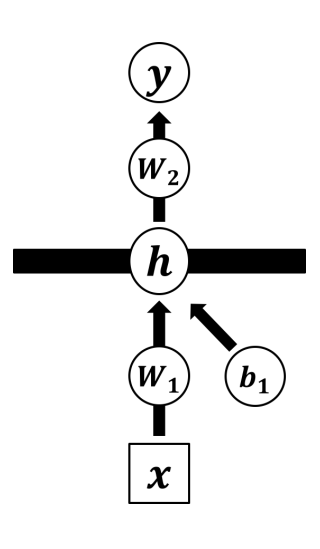
N(yd;0,ΦΦT+τ−1)=∫N(yd;0,Φwd+τ−1I)N(wd;0,I)dwd
P(Y∣X)=∫P(Y∣X,w1,...wd,b)p(w1)...p(wd)p(b)dw1...dwddb
d개의 layer를 통해서 구한 likelihood를 recon error에 활용하여 ELBO를 최대화하는 문제를 해결할 수 있습니다. 하지만 해당 방법은 Neural network로 문제를 해결하는 것보단, GP prior로 문제를 해결한 것이라고 볼 수 있습니다. 따라서 다음 포스트에서는 VAE 모델을 중점으로 Neural network에서 변분 추론이 어떻게 이루어지는지 알아보겠습니다.
Reference
[1] Bayesian Deep Learning, 최성준, https://www.edwith.org/bayesiandeeplearning/joinLectures/14426
[2] Pattern recognition and machine learning, https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
[3] Kernel method, Wikipeida, https://en.wikipedia.org/wiki/Kernel_method



