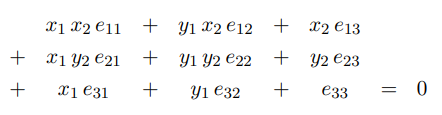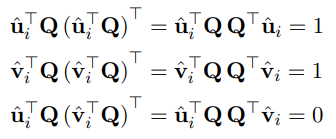COLMAP의 SFM 파이프라인입니다. 크게 두 부분으로 나눠지는데, Correspondence Search와 Incremental Reconstruction입니다. Correspondence Search는 2D features를 찾고, 이미지 사이의 이들을 매칭하는 단계입니다. Incremental Reconstruction은 매칭된 피쳐들이 3D structure와 카메라 파라미터들로 사용되는 단계입니다. SFM의 대략적인 구조를 살펴보았으니, 필요한 개념들을 알아보겠습니다. (매우 많습니다..)
Camera Calibration
Camera Calibration은 카메라 셋업의 내부(intrinsic), 외부(extrinsic) 파라미터를 찾는 과정이며, 2D 이미지셋으로 3D 구조 정보를 추론할 때 매우 중요합니다. (Computer Vision 개념 정리! (velog.io): 관련 CV 개념을 정리해놓은 포스트입니다!)
- 대부분의 경우, 이미 타겟을 알고 있는 체커보드에서 캘리브레이션을 사용합니다. 다양한 각도의 체커보드 이미지를 준비하는 것이 첫 단계입니다.

- 코너와 같은 features를 이미지에서 찾습니다.
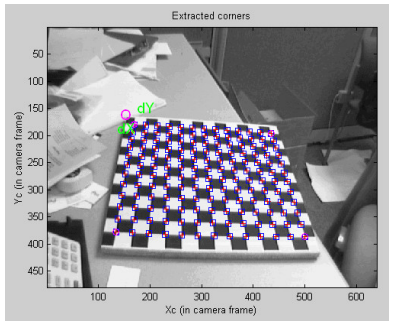
- 카메라 내부, 외부 파라미터를 공동으로 최적화합니다. Closed-form solution으로 모든 파라미터들 초기화 후(distortion 파라미터들은 이때 제외입니다.) Non-linear optimization으로 모든 파라미터들을 얻어냅니다.
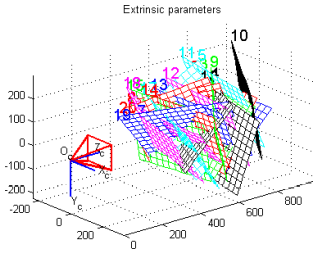
Calibration Code (OpenCV)
import numpy as np
import cv2 as cv
import glob
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)
objpoints = []
imgpoints = []
images = glob.glob('*.jpg')
for fname in images:
img = cv.imread(fname)
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, corners = cv.findChessboardCorners(gray, (7,6), None)
if ret == True:
objpoints.append(objp)
corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
imgpoints.append(corners2)
cv.drawChessboardCorners(img, (7,6), corners2, ret)
cv.imshow('img', img)
cv.waitKey(500)
cv.destroyAllWindows()
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
OpenCV에서 제공하는 코드는 다음과 같습니다.
cv.findChessboardCorners 함수로 체커보드의 코너를 찾고, cv.cornerSubPix 함수로 체커보드의 코너들을 조정합니다. 이후 찾아낸 이미지 코너들과 3D 포인트들을 활용하여 Camera의 파라미터들을 찾아내는 과정입니다.
카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습
OpenCV: Camera Calibration
www.microsoft.com
Feature Detection

Point features는 이미지의 local, salient regions을 표현합니다. point features를 활용하여 다른 viewpoints를 가지는 이미지들을 매칭하는 것이 가능합니다!
Features는 원근 효과나 조도에 영향을 받지 않아야 하고, 같은 포인트는 pose나 viewpoint와 관계 없이 비슷한 벡터를 가져야 합니다.
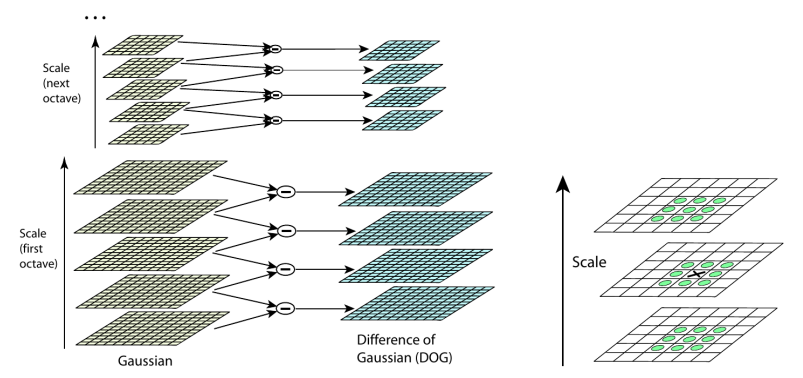

SIFT는 반복적으로 이미지를 가우시안 필터링하여 scale space를 구성하고, 이미지를 일정한 간격으로 축소시킵니다. 인접한 스케일을 빼면, Difference of Gaussian(DoF) 이미지들이 생성됩니다. DoG로 blobs가 발견되며 scale space에서 extrema로 나타납니다.
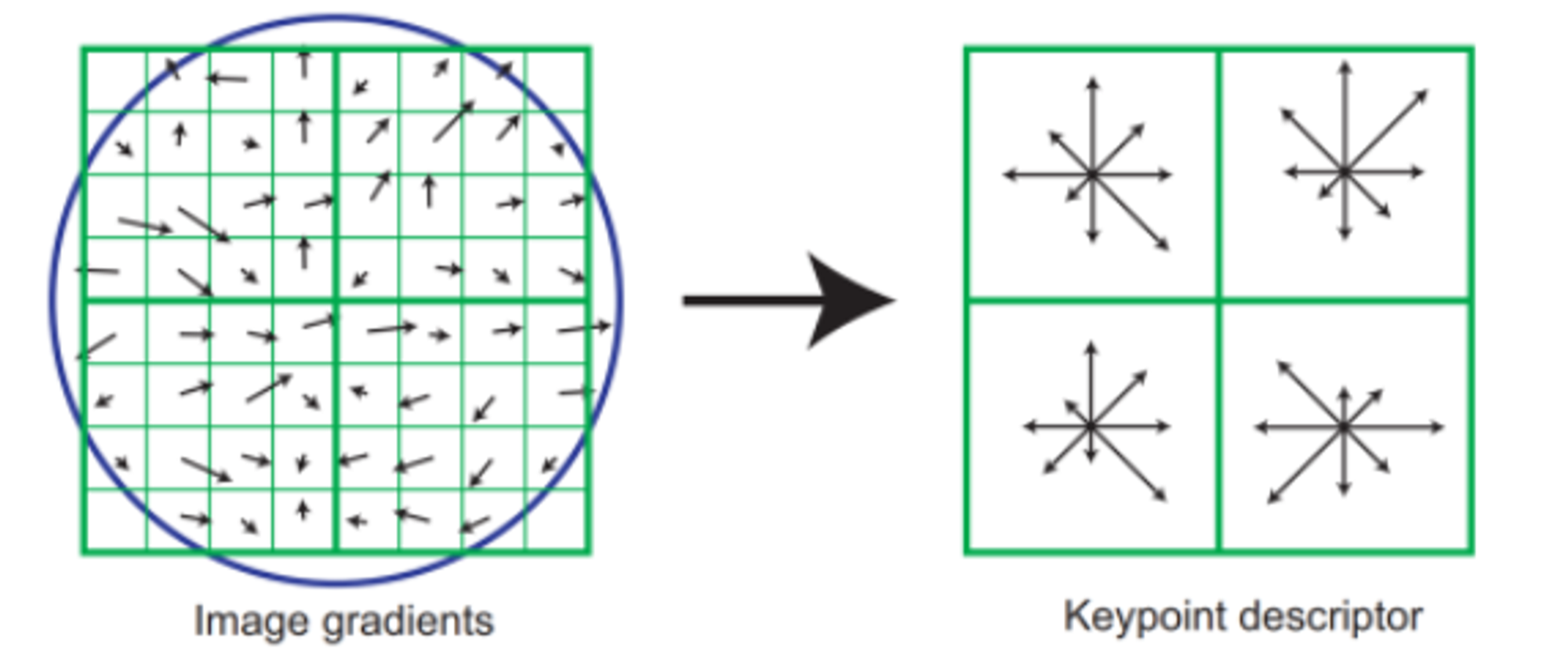
blobs를 추출하고 나면, discriptor를 회전시켜 주요한 gradient 방향과 일치시킵니다. 이후 128D feature vector(Keypoint descriptor)를 형성하는 데 사용되는 gradient histogram이 계산됩니다.

SIFT는 20년이 지남에도 불구하고, COLMAP에서 아직도 사용되고 있습니다. 위 사진은 두 이미지에 SIFT를 적용한 예시입니다. (초록: 정답 / 빨강: 오답)
Epipolar Geometry
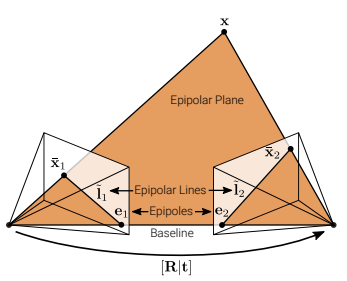
epipolar geometry의 목적은 이미지 상관관계로부터 camera pose와 3D structure 정보를 얻는 것입니다. 자세히 알아보기 전, 표현들부터 짚어보겠습니다.
- x: a 3D point
- xˉ: 이미지 평면에 사영된 point
- Baseline: 두 카메라 센터를 지나는 선
- epipole: Baseline이 이미지 평면과 만나는 point
- epipolar line: epipolar plane과 image plane이 만나는 교차선
two-view epipolar geometry를 적용하기 위한 조건은 다음과 같습니다. (개인적으로는 그림으로 파악하는 것이 이해하기 쉬웠습니다.)
- R과 t가 두 카메라에 정의되어 있음.
- a 3D point x가 pixel xˉ1과 pixel xˉ2에 놓여 있어야 함.
- a 3D point x와 두 카메라 센터가 epipolar plane 구성.
- pixel xˉ1에 대응되는 pixel(xˉ2)이 epipolar line l~2에 놓여 있어야 함.
- 모든 epipolar lines이 epipole을 통과.
Estimate epipolar geometry
두 이미지간의 매칭된 features로 epipolar geometry를 추정하는 과정을 유도해보겠습니다.
방법 (1)
- Ki∈R3×3: camera matrix of camera i ← calibration!
- x~i=Ki−1xˉi: local ray direction of pixel xˉi
위 두 가지 조건을 사용하면 다음의 비례식을 얻을 수 있습니다.
x~2∝x2=Rx1+t∝Rx~1+st
양쪽에 t로 외적을 취하면 다음과 같습니다.
[t]×x~2∝[t]×Rx~1
이후 양쪽에 x~2T로 내적을 취하면 다음과 같습니다.
x~2T[t]×x~2=0∝x~2T[t]×Rx~1→x~2T[t]×Rx~1=0
이를 essential matrix로 정리하여 표현하면 epipolar constraint를 얻을 수 있습니다.
x~2TE~x~1=0
- essential matrix: E~=[t]×R
- E~ 는 point x~1를 epipolar line in image 2로 매핑하는 것이 가능합니다. (반대로도 가능!) l~2=E~x~1
임의의 점 x~1에 대해 대응하는 epipolar line l~2=E~x~1은 epipole e~2를 지나게 되며, 다음의 식을 만족합니다.
e~2Tl~2=e~2TE~x~1=0.→e~2TE~=0.
- 위 식을 통해서 e~2T가 E~의 left null-space임을 알아낼 수 있습니다. (left singular vector with singular value 0 or smallest value{noise때문에 0이 아닐 수도 있음!})
- 반대로, e~1T가 E~의 right null-space입니다. (right singular vector with singular value 0)
방법 (2)
x~2∝x2=Rx1+t
이때 Rx1+t와 t는 epipolar plane에 놓여 있으므로, 외적을 취하면 plane에 직교하는 평면 벡터 [t]×Rx1를 구할 수 있습니다. 이는 x2T와의 내적을 취하면 해당 값이 0으로 나오고, 이를 통해 epipolar constraint를 얻을 수 있습니다. (해당 설명은 K가 I일 때로 가정되었지만, 이외에도 적용 가능합니다.)
8-point algorithm
앞에서 얻은 epipolar constraint를 가지고, N개의 이미지 쌍에 대해 다음의 방정식을 구할 수 있습니다.
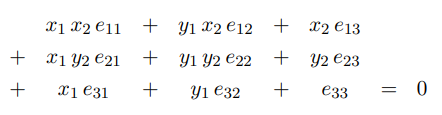
이를 SVD를 통해 해결할 수 있으며, 8개의 쌍으로 해결하는 것이 가능하기 때문에 8-point algorithm으로 불립니다.
Fundamental matrix
위의 과정을 통해 E~를 구할 수 있으며, t^와 R을 차례로 구할 수 있습니다. (해당 과정의 증명은 아래에 남겨두었습니다.)
calibration metrix Ki∈R3×3를 식에 대입하여 fundamental matrix를 표현하면, Intrinsic matrix 없이도 epipoles를 구할 수 있습니다.
x~2TE~x~1=xˉ2TK2TE~K1−1xˉ1=xˉ2TF~xˉ1=0.
- F~=K2TE~K1−1: fundamental matrix
- fundamental matrix, essential matrix 모두 2 Rank의 행렬임!!
Demo of epipolar geometry

- epipolar lines: 검정색 라인
- 대응되는 점은 대응되는 epipolar line에 놓여 있음!
Triangulation
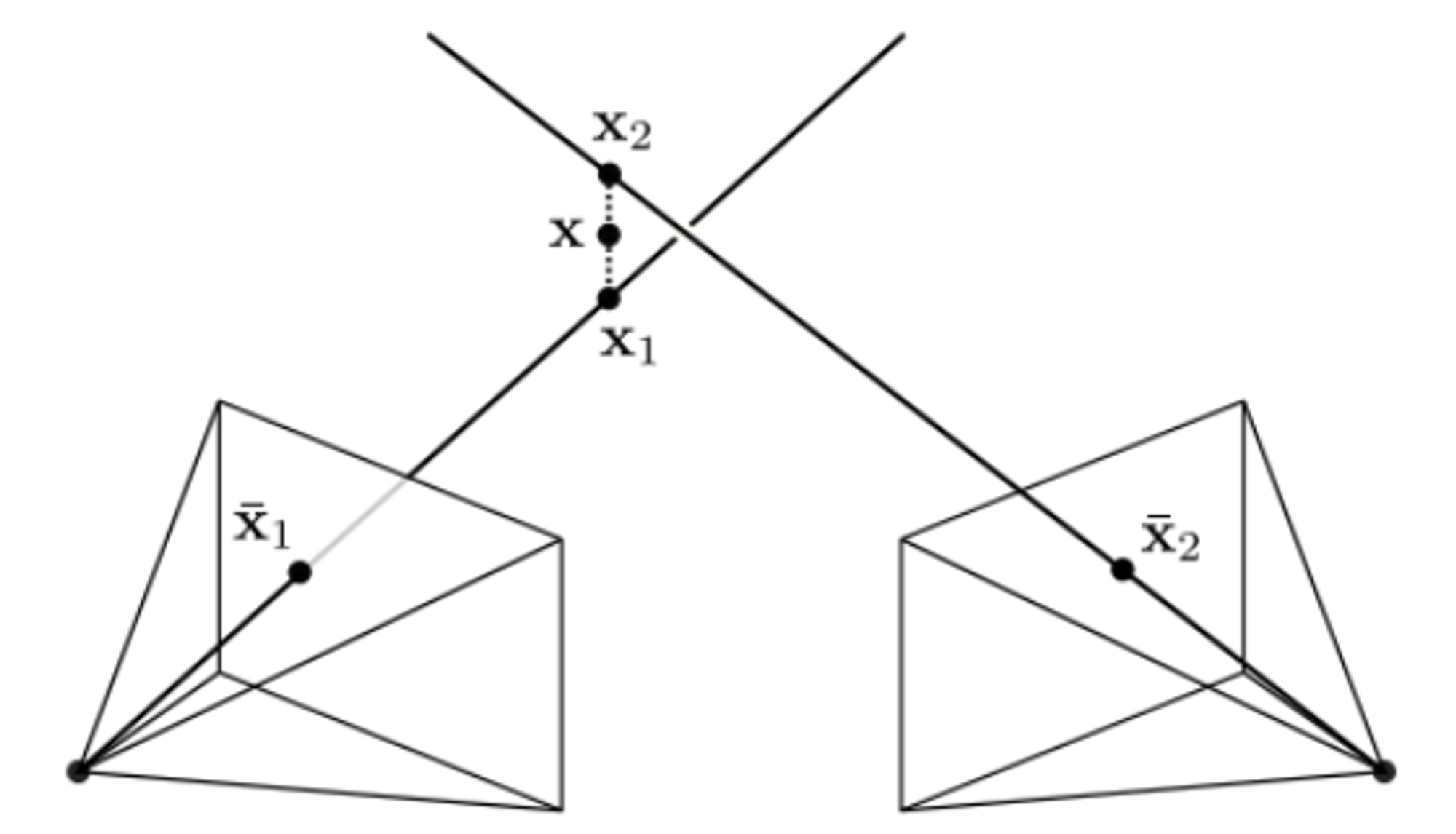
만약 2D 이미지 관측이 주어졌을 때, 두 rays가 교차하지 않는 경우를 살펴보겠습니다.
- x~is=P~ix~w: projection (3D world point x~w → i번째 카메라 x~is의 이미지)
- 양쪽 벡터가 homogeneous → 두 벡터가 같은 방향임 → x~is×P~ix~w=0. → 아래의 식 유도 가능!
[xisp~i3T−p~i1Tyisp~i3T−p~i2T]x~w=0
- Ai=[xisp~i3T−p~i1Tyisp~i3T−p~i2T]
- p~ikT: k번째 행 벡터 of P~i
DLT(링크)를 통해 이를 least square 문제로 해결할 수 있습니다. 마찬가지로, A의 singular value 중 가장 작은 값에 해당하는 right singular vector가 최적의 해가 됩니다. 이것은 reprojection error를 최소화하는 것과 같은 의미를 가지기도 합니다.
xˉw∗=xˉwargmini=1∑N∣∣xˉis(xˉw)−xˉio∣∣22
- xˉio: observation
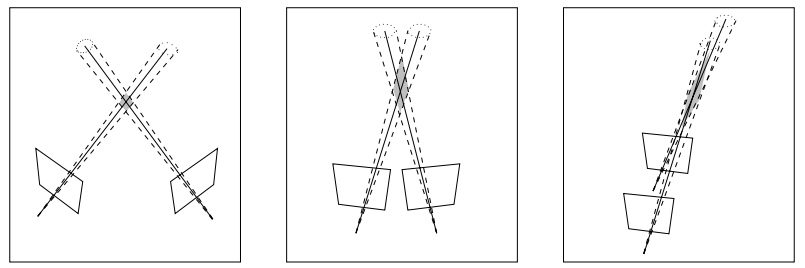
- rays가 평행할수록 Uncertainty(shaded region) 증가
- Tradeoff: view가 가까울수록 feature matching은 쉬움 / triangulation은 어려워짐
Factorization
이번 챕터에서는 2개 이상의 views로 3D geometry를 형성하는 과정을 살펴보겠습니다.
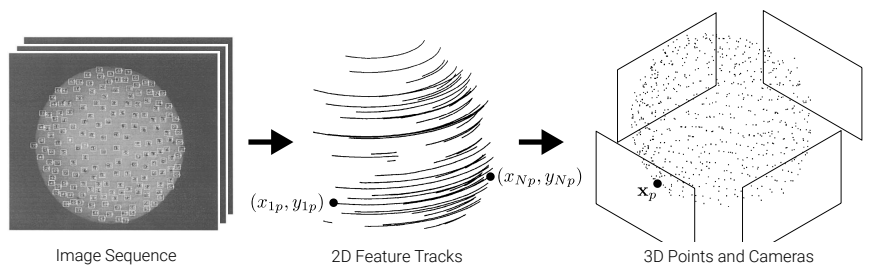
- W={(xip,yip)∣i=1,...,N,p=1,...,P}u: P feature points tracked over N개의 프레임
- W와 orthographic projection을 통해서
camera motion (rotation), structure(3D points xp ← (xip,yip))을 구하는 것이 목표!
Orthographic Factorization
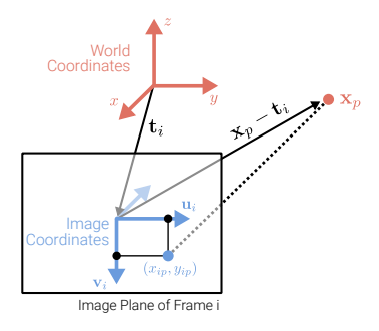
- orthographic projection: a 3D points xp → a pixel (xip,yip) in frame i
xip=uiT(xp−ti)yip=viT(xp−ti)
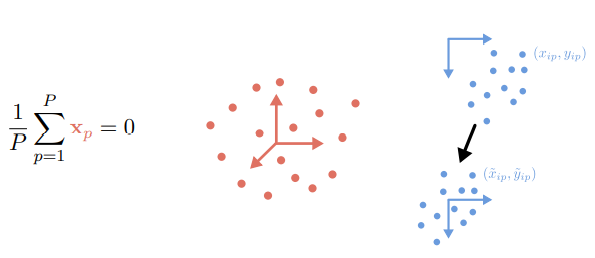
- 3D 좌표계(빨간색), 이미지 좌표계(파란색) 모두 centering ! (zero-mean) → frame 마다 이미지 피쳐들도 센터링하여 centered measurement matrix W~를 얻을 수 있음.
W~=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡x~11⋮x~N1y~11⋮y~N1............x~1P⋮x~NPy~1P⋮y~NP⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
- x~ip=xip−P1∑q=1Pxiq
- y~ip=yip−P1∑q=1Pyiq
- 이때 ~는 homogeneous를 의미하지 않음 -> centered 의미!
위 성질들을 이용하여 centered image x 좌표를 다음과 같이 구할 수 있습니다.
x~ip=xip−P1q=1∑Pxiq=uiT(xp−ti)−P1q=1∑PuiT(xq−ti)=uiT(xp−ti)−uiTP1q=1∑Pxq+uiTti=uiT(xp−P1q=1∑Pxq)=uiTxp
- centered image y 좌표: y~ip=viTxp
따라서 centered measurement matrix W~도 다음과 같이 분해할 수 있습니다.
W~=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡x~11⋮x~N1y~11⋮y~N1............x~1P⋮x~NPy~1P⋮y~NP⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=RX
-
R=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡u1T⋮uNTv1T⋮vNT⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤∈R2N×3: camera motion (rotation)
-
X=[x1...xP]∈R3×P: structure of the 3D scene
W~는 대부분 rank 3입니다. 만약 noise가 추가되면, full rank이며 rank 3 approximation을 적용합니다.
(||W^−W~||를 최소화하는 방향으로 근사. / SVD로 구할 수 있음 !!)
W^=UΣVT=RX=(R^Q)(Q−1X^)
- R^=UΣ21
- X^=Σ21VT
이때 행렬 Q에 따라 SVD 분해가 여러 개가 등장할 수 있기 때문에 행렬 조건들을 몇 가지 적용해야 합니다. R의 두 가지 특성을 이용하여 행렬 조건을 세운 것이 아래 사진입니다.
- R의 행 벡터가 단위 벡터입니다.
- R의 첫 번째 절반(about u)과 두 번째 절반(about v)은 직교 상태입니다.
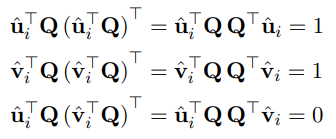
이 제약 조건을 통해 Q를 구하여 unique solution을 구하게 됩니다.
Algorithm
Orthographic factorization을 정리하면 다음과 같습니다.
- W^를 측정합니다.
- W^의 SVD를 계산한 후, top 3 Singular vectors를 얻습니다.
- R^=UΣ21, X^=Σ21VT를 정의합니다.
- QQT를 계산하여 Q를 구합니다.
- R=R^Q, X=Q−1X^를 구합니다.
Bundle Adjustment
incremental bundle adjustment는 선택된 two-view recon으로부터 반복적으로 새로운 이미지/카메라를 reconstruction에 추가하는 알고리즘입니다. (COLMAP에서는 BA를 사용하고 있습니다.)
- Π={πi}: N cameras with intrinsic, extrinc params
- Xw={xpw}∈R3: set of P 3D points (world coord!)
- Xs={xips}∈R2: image(screen) observations
BA는 아래의 reprojection error를 최소화하는 방향으로 최적화됩니다. Projection은 non-linear하기 때문에, 비선형적 최적화가 이루어집니다.
Π∗,Xw∗=Π,XWargmini=1∑Np=1∑Pwip∣∣xips−πi(xpw)∣∣22
- wip: point p가 이미지 i에서 관찰되었는지 나타내는 역할
- πi(xpw): 3D-to-2D projection of 3D world point xpw
- xps~=Ki(Rixpw+ti) → πi(xpw)=(xps~/wps~yps~/wps~)
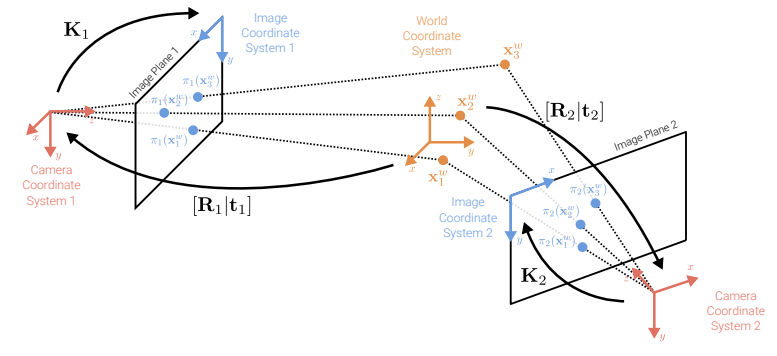
Incremental Structure-from-Motion

SFM에 해당 개념들이 적용되는 것을, SFM pipeline에 맞춰서 살펴보는 것으로 포스트를 마무리하겠습니다!
Correspondence Search
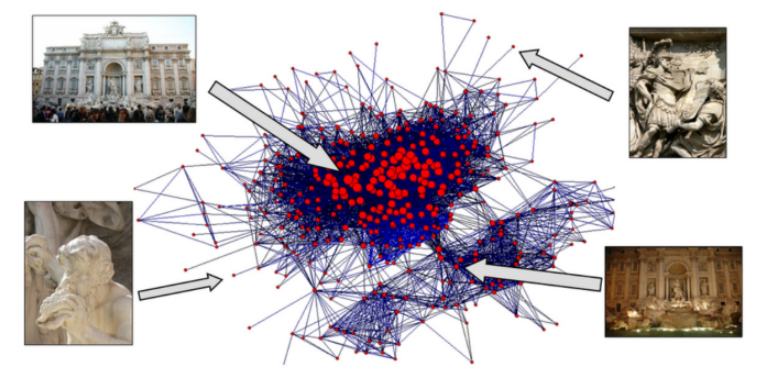
(1) Feature matching (using SIFT)
(2) Geometric Verification (feature association!)
Incremental Reconstruction
(0) Inintialization → two-view를 선택한 후 epipolar geometry를 계산
(1) Image Registration: 현재 이미지 셋에 대한 새로운 이미지들 추가 + camera pose 추정 → DLT로 projection matrix P구하기
(2) Triangulation: 새로운 이미지에 대해 적용
(3) Bundle Adjustment + Outlier Filtering: reprojection error 최소화! / local로 연결된 이미지들에 대해 BA 적용. global BA는 한 번만 적용.
Reference
[1][Prof. Dr. Andreas Geiger](https://uni-tuebingen.de/fakultaeten/mathematisch-naturwissenschaftliche-fakultaet/fachbereiche/informatik/lehrstuehle/autonomous-vision/team/), Computer vision (2023)
[2] https://web.stanford.edu/class/cs231a/course_notes/03-epipolar-geometry.pdf