목차
트리란
-
트리 (Tree)란 노드들이 나무 가지처럼 연결된
비선형 계층적 자료구조입니다 -
트리는
재귀적 자료구조이기도 합니다. 트리안에 트리, 트리 안에 트리, ... -
하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있습니다. -
단순 순환(Loop)을 갖지 않고,
연결된 무방향 그래프 구조입니다. -
노드 간에 부모 자식 관계를 갖고 있는
계층형 자료구조이며 모든 자식 노
드는하나의 부모 노드만 갖습니다. -
노드가 n개인 트리는 항상 n-1개의 간선(edge)을 가집니다.
-
컴퓨터의 디렉토리, 회사 조직도, 검색엔진, Dom 구조 등 다양하게 사용된다.
트리용어
노드 (Node)

트리를 구성하고 있는 기본 요소- 노드에는
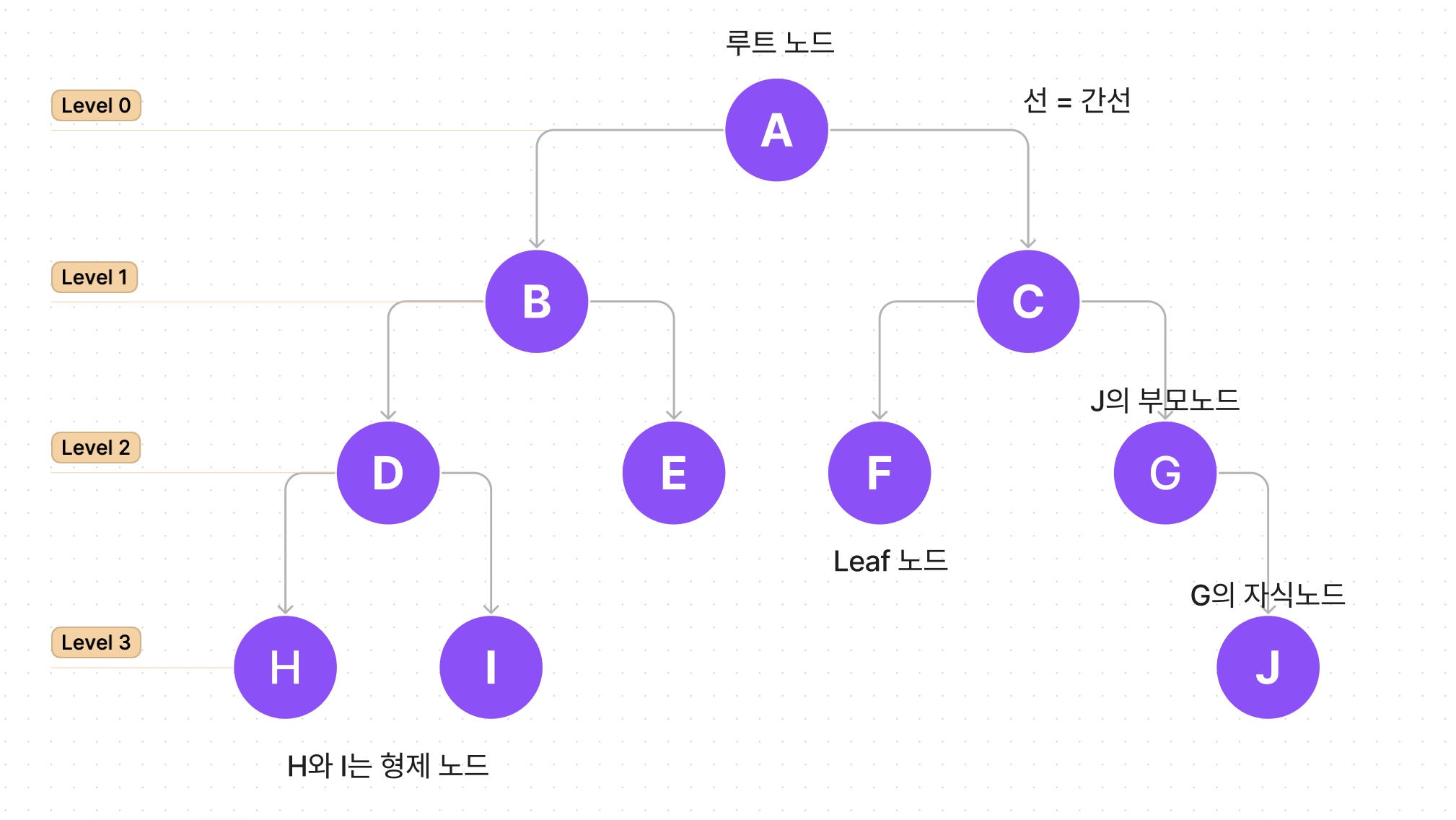
키(값)과 하위 노드에 대한 포인터를 가지고 있습니다. - A, B, C, D, E, F, G, H, I, J 모두 노드입니다.
-
간선 (Edge)
-
-
노드와 노드 간의 연결선입니다. -
link 또는 branch라고도 부릅니다.
-
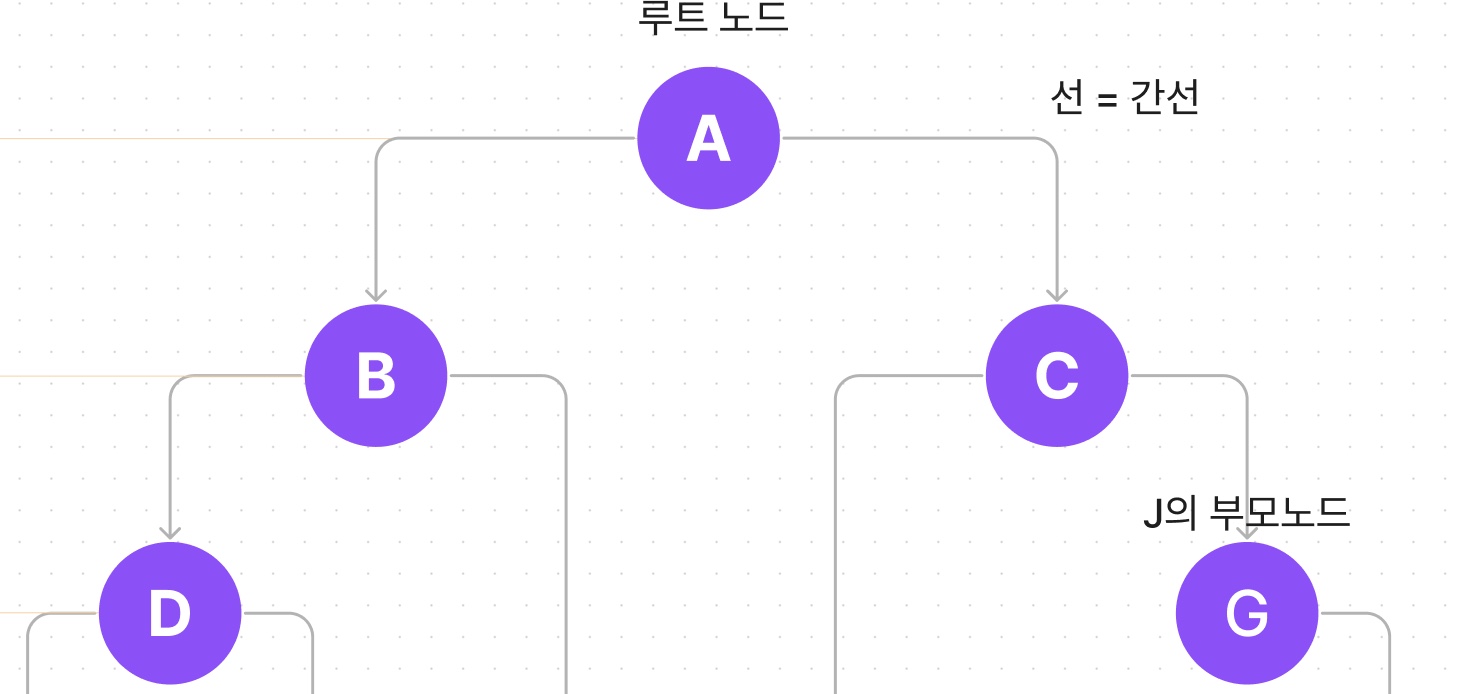
루트 노드 (Root Node)

부모가 없는 노드이며, 트리는 하나의 루트 노드만을 가집니다!A가 루트 노드 (Root Node)입니다.
부모 노드 (Parent Node)
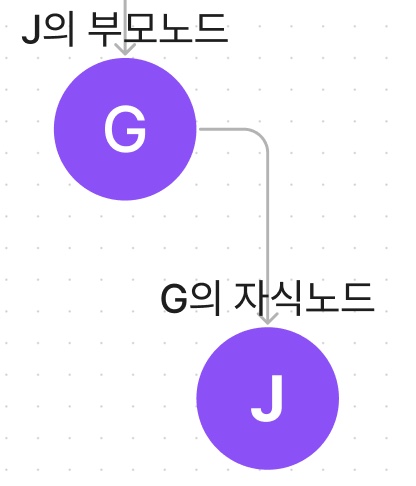
자식 노드를 가진 노드입니다.G는 J의부모노드입니다.
자식 노드 (Child node)

부모 노드의 하위 노드입니다.J는 G의자식노드입니다.
형제 노드 (Sibling node)

같은 부모를 가지는 노드입니다.H와 I는 형제노드입니다. D라는 같은 부모를 가지기 때문입니다.
단말 노드 (terminal node)
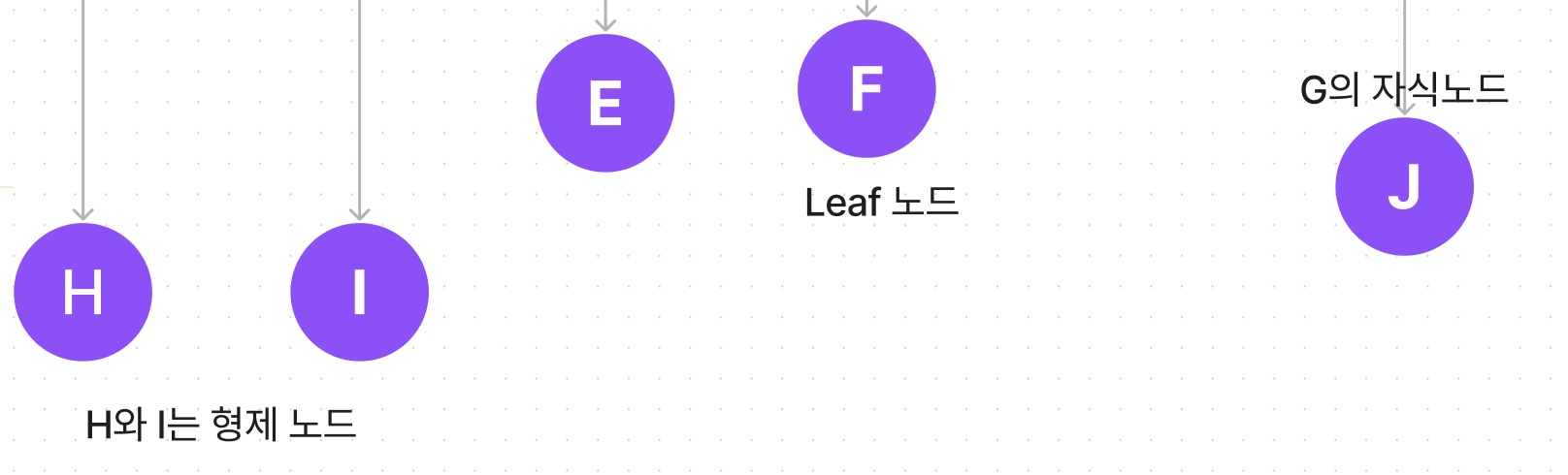
자식 노드가 없는 노드입니다.외부 노드(external node, outer node) 또는 리프 노드(leaf node)라고도 합니다.H, I, E, F, J를 단말노드라고 합니다.
비 단말 노드 (non-terminal node)
자식 노드를 하나 이상 가진 노드입니다.내부 노드 (internal node, inner node), 가지 노드 (branch node)라고도 합니다.A, B, C, D, G를 비 단말노드라고 합니다.
깊이 (depth)

루트에서 어떤 노드까지의 간선(Edge) 수입니다.루트 노드의 깊이는 0입니다.D의 깊이는 2,H의 깊이는 3입니다.
높이 (height)

어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수입니다.리프 노드의 높이는 0입니다.A 노드의 높이는 3,B의 높이는 2입니다.
레벨 (Level)

루트에서 어떤 노드까지의 간선(Edge) 수입니다.리프 노드의 레벨은 0입니다.B의 레벨은 1,D의 레벨은 2입니다.
차수(Degree)

노드의 자식 수입니다.Leaf node의 차수(degree)는 0입니다.A의 차수(degree)는 2, G의 차수(degree)는 1입니다.
경로 (Path)

한 노드에서 다른 노드 사이에 놓여있는 노드들의 순서입니다.A에서 H까지의 경로는 A-B-D-H입니다.
크기 (Size)

자신을 포함한 자손의 노드 수입니다.노드 B의 size는 5, 노드 C의 Size는 4입니다.
넓이 (Width)

해당 레벨에 있는 노드 수입니다.Level 2의 width는 4 , Level 3의 width는 3입니다.
Breadth

리프 노드의 수입니다.Breadth는 5입니다.
Distance

두 노드 사이의 최단 경로에 있는 간선(Edge)의 수입니다.F와 J의 Distance는 3입니다.
Order
부모 노드가 가질 수 있는 최대 자식의 수입니다.Order 3이면 부모 노드는 최대 3명의 자식을 가질 수 있습니다.
트리의 종류
이진트리(Binary Tree)
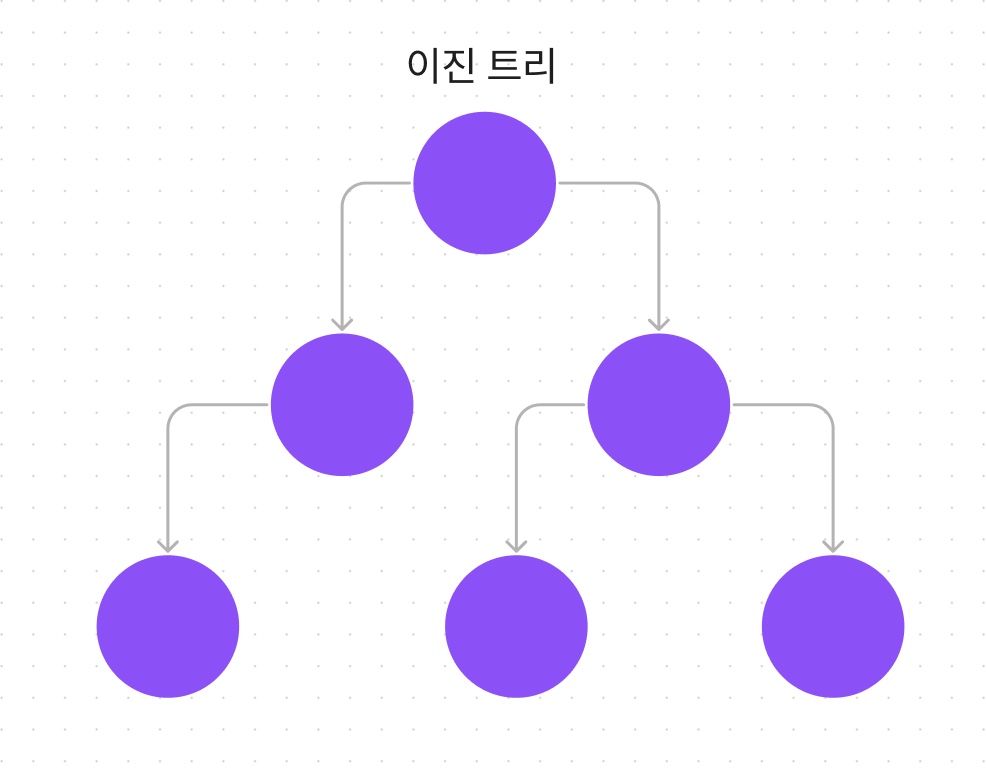
자식 노드가 최대 2개까지만 허용하는 트리- 모든 트리가 이진트리는 아닙니다.
완전 이진 트리 (Complete Binary Tree)
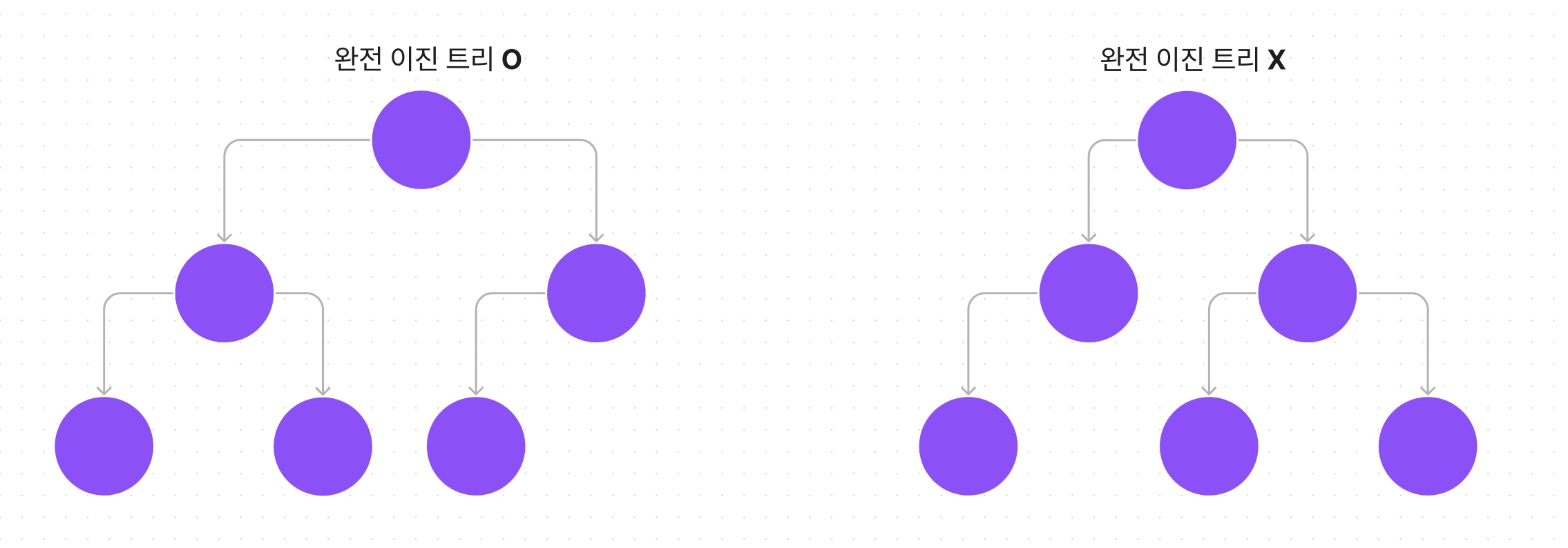
마지막 레벨을 제외한 모든 노드는 완전히 채워져 있어야 하며, 왼쪽에서 오른쪽으로 순서대로 차곡차곡 채워져있는 이진 트리
포화 이진 트리 (Perfect Binary Tree)
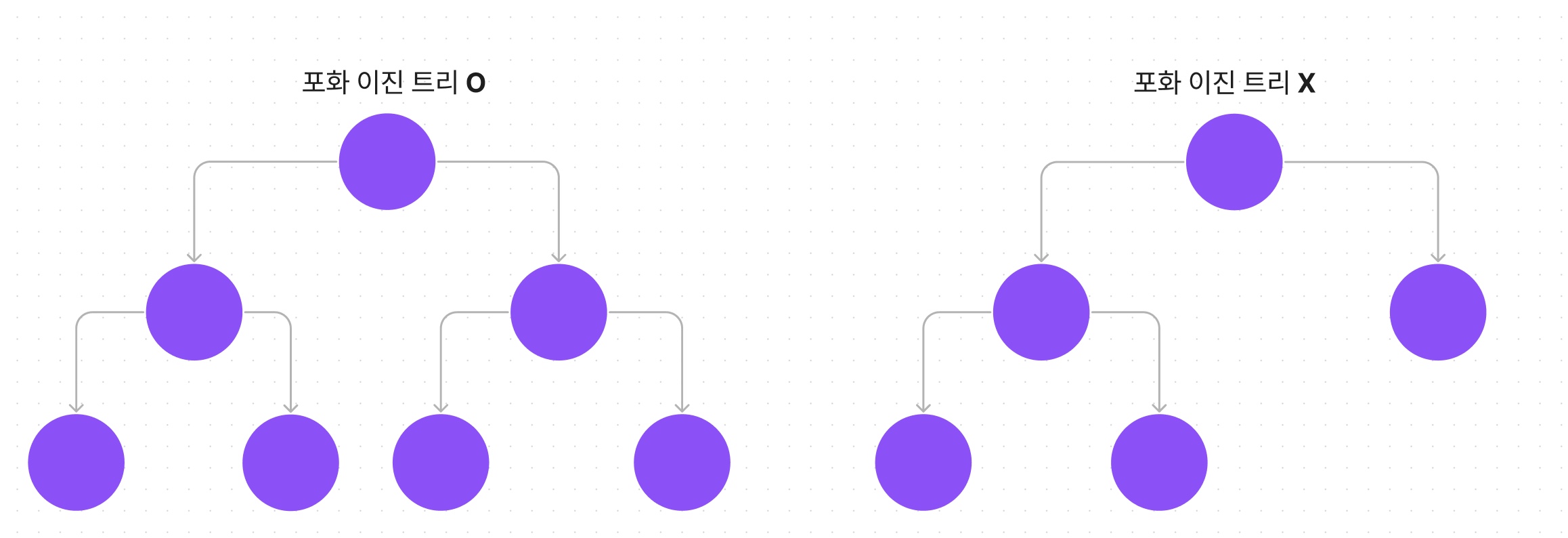
모든 노드의 차수가 2이며 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 이진트리
-
전 이진 트리 (Full Binary Tree)
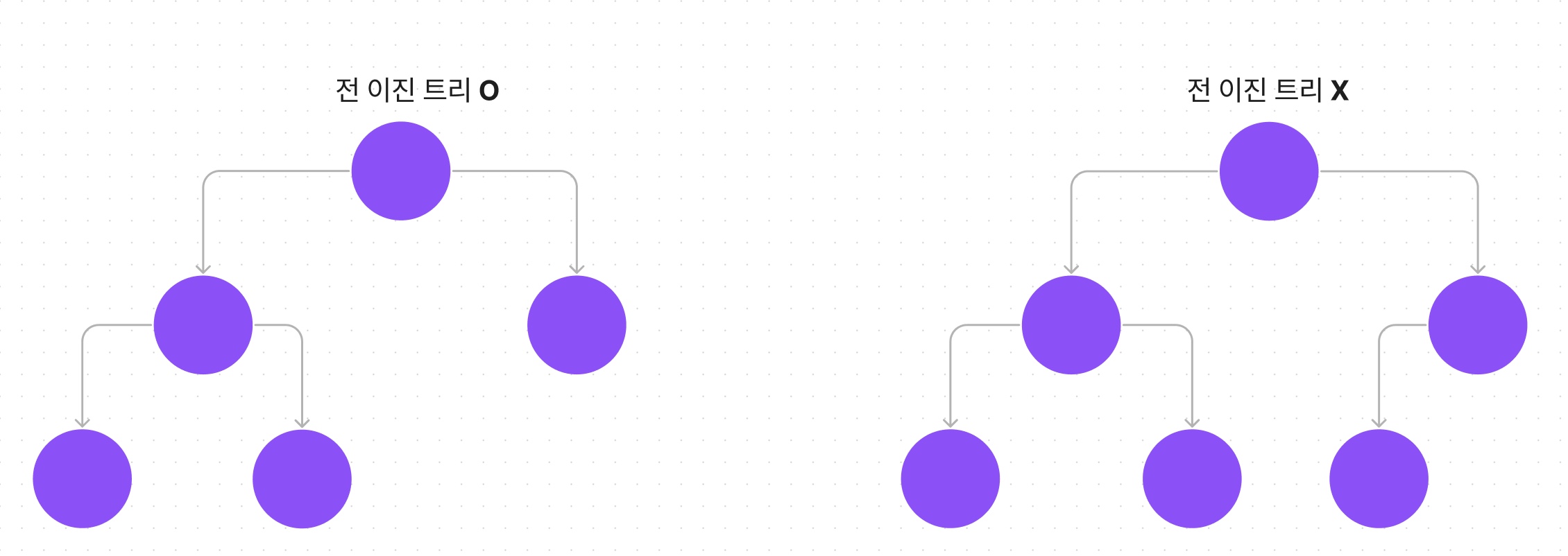
모든 노드의 차수가 2 혹은 0인 이진 트리
-
이진 탐색 트리(Binary Search Tree)
-
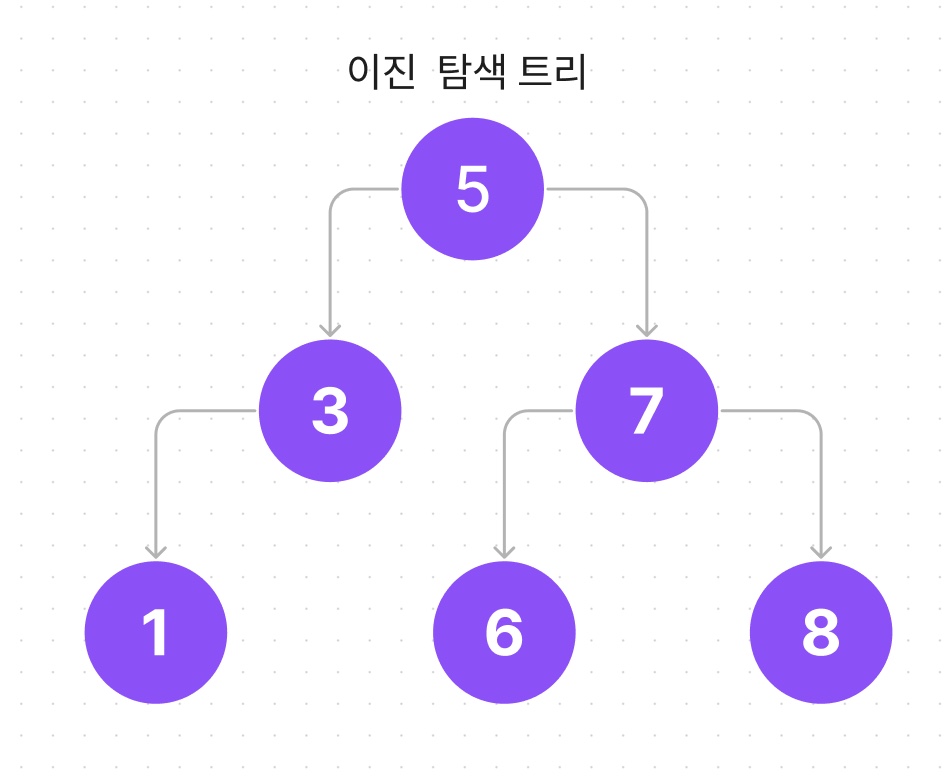
-
이진탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조의 일종으로서
이진 트리를 이용한 검색 방법을 이용할 때 쓰는 트리구조입니다. -
부모노드의
왼쪽 자식 노드에는 부모노드보다작은 값이,
오른쪽 자식 노드에는 부모 노드보다큰 값이들어가 있어야 하며,중복된 노드가 없어야 하는트리입니다.
-
-
삼항트리 (Ternary Tree)
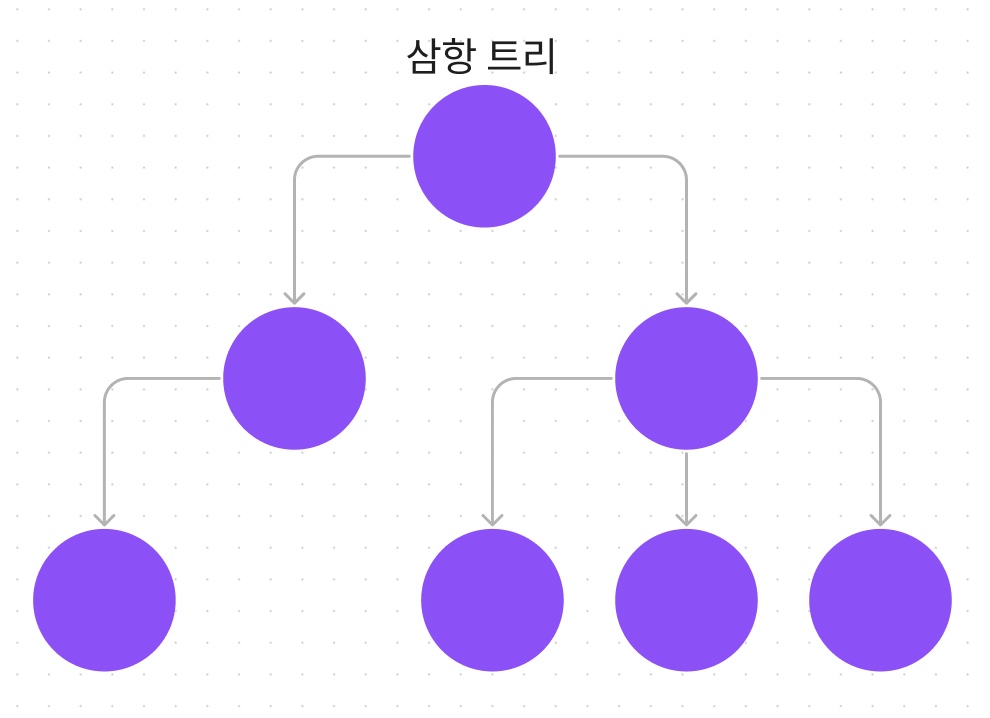
자식 노드가 3개 이상 존재하는 트리
편향 이진 트리 (Skewed Binary Tree)
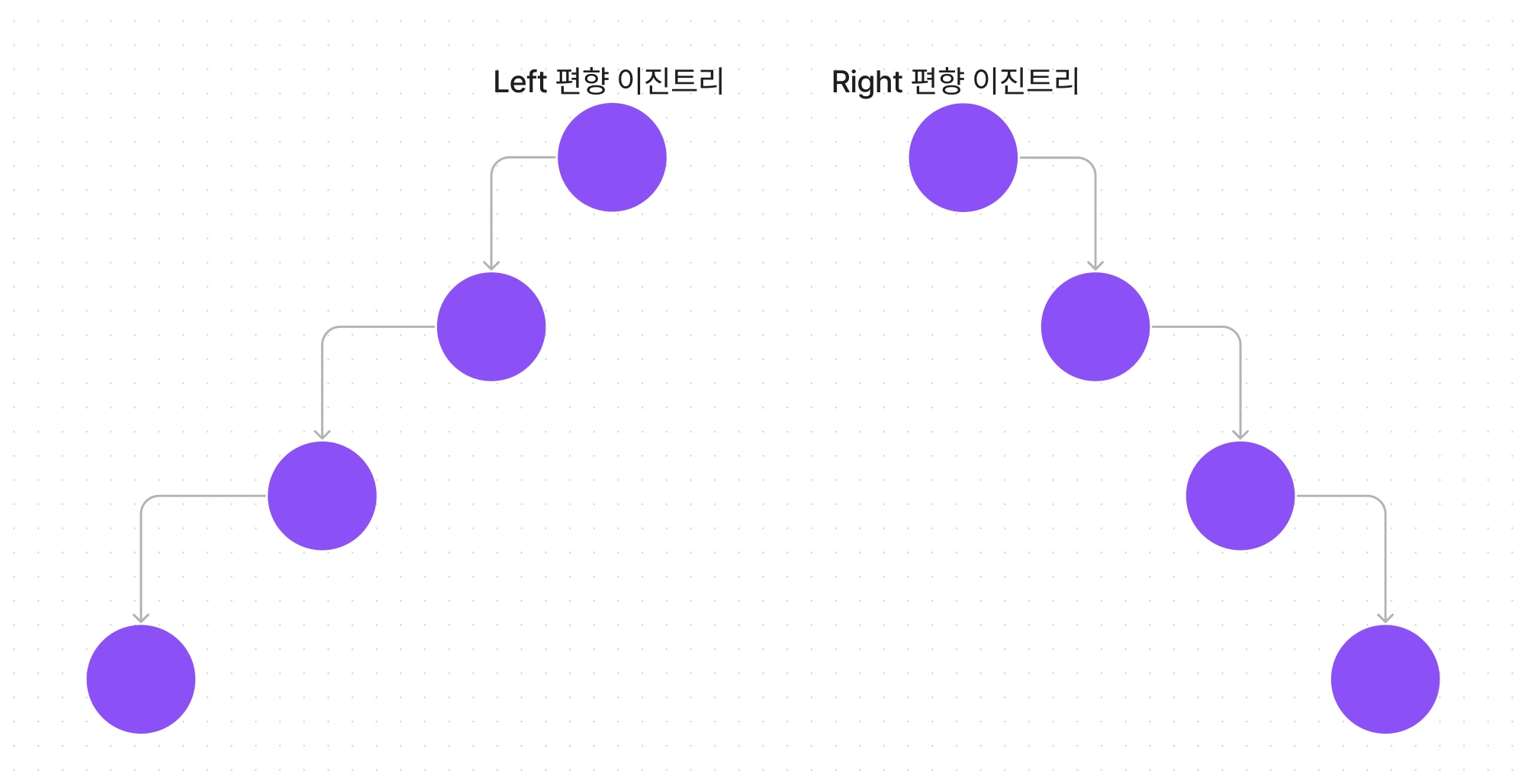
모든 노드가 부모의 왼쪽 혹은 오른쪽으로 편향되어 있는 트리
트리의 순회
-
트리의 순회란 트리의모든 노드들을 방문하는 과정을 의미합니다. -
선형 자료 구조(연결 리스트, 스택, 큐 등)는 순차적으로 요소에 접근하지만
트리 자료구조는 3가지의 순회 방법을 통해 요소에 접근할 수 있습니다. -
전위 순회 (Preorder Traversal)
-
전위 순회는 깊이 우선 순회(DFT, Depth-First Traversal)라고 하기도 합니다.
-
트리를 복사할 때 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문에, 주로 트리를 복사하거나, 전위 표기법을 구하는데 사용합니다.
-
전위 순회 순서
- 루트 노드를 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위 순회한다.
-
아래의 그림에서
전위 순회 순서는 5-3-1-7-6-8입니다.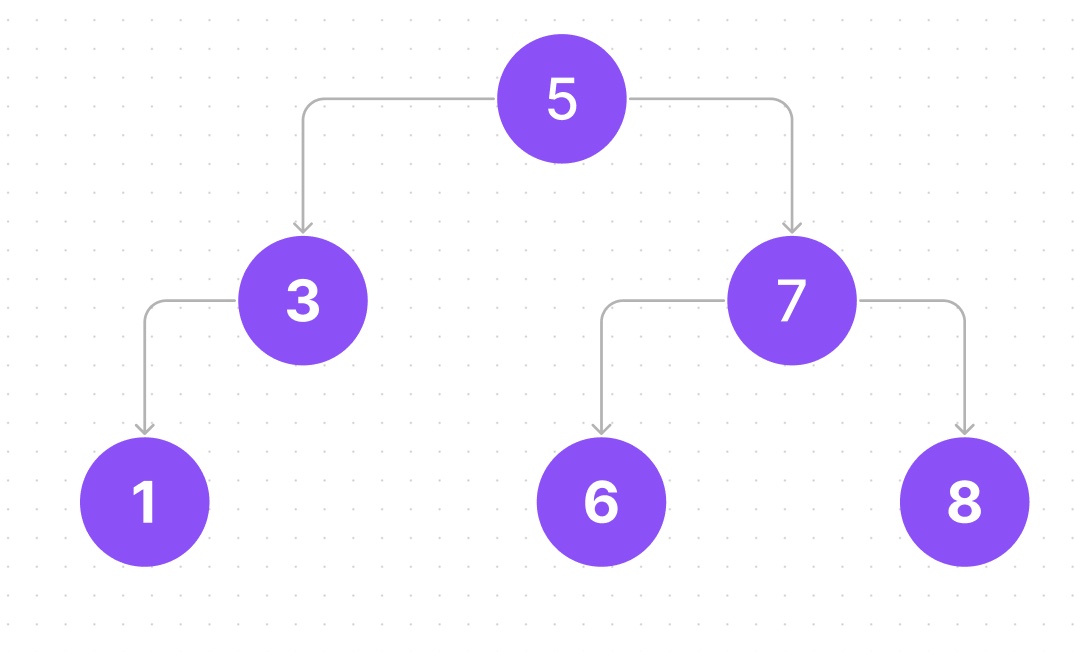
-
-
중위 순회 (Inorder Traversal)
-
중위 순회는 왼쪽 오른쪽 대칭 순서로 순회를 하기때문에
대칭 순회(symmetric traversal)라고도 합니다. -
중위 순회 순서
- 왼쪽 서브 트리를 중위 순회한다.
- 루트 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
- 아래의 그림에서
중위 순회 순서는 1-3-5-6-7-8입니다.

-
-
후위 순회 (Postorder Traversal)
-
부모 노드보다 자식 노드를 먼저 탐색하기 때문에 후위 순회는 주로
트리를 삭제할때 사용합니다. -
후위 순회 순서
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 루트 노드를 방문한다.
- 아래의 그림에서
후위 순회 순서는 1-3-6-8-7-5입니다.

-
JS로 트리 구현하기
class Tree {
constructor(val) {
this.val = val;
this.leftNode = null;
this.rightNode = null;
}
getVal() {
return this.val;
}
setVal(val) {
this.val = val;
}
addLeftNode(node) {
this.leftNode = node;
}
getLeftNode(node) {
return this.leftNode;
}
addRightNode(node) {
this.rightNode = node;
}
getRightNode(node) {
return this.rightNode;
}
// 전위순회
preOrderTraversal(node) {
if (!node) {
return;
}
console.log(node.val);
this.preOrderTraversal(node.leftNode);
this.preOrderTraversal(node.rightNode);
}
// 중위순회
inOrderTraversal(node) {
if (!node) {
return;
}
this.inOrderTraversal(node.leftNode);
console.log(node.val);
this.inOrderTraversal(node.rightNode);
}
// 후위순회
postOrderTraversal(node) {
if (!node) {
return;
}
this.postOrderTraversal(node.leftNode);
this.postOrderTraversal(node.rightNode);
console.log(node.val);
}
}
let root = new Tree(5);
let node = new Tree(3);
root.addLeftNode(node);
node = new Tree(7);
root.addRightNode(node);
node = new Tree(1);
root.leftNode.addLeftNode(node);
node = new Tree(6);
root.rightNode.addLeftNode(node);
node = new Tree(8);
root.rightNode.addRightNode(node);
console.log('start preOrder');
root.preOrderTraversal(root); // 5-3-1-7-6-8
console.log('');
console.log('start inOrder');
root.inOrderTraversal(root); // 1-3-5-6-7-8
console.log('');
console.log('start postOrder');
root.postOrderTraversal(root); // 1-3-6-8-7-5
console.log('');