자료구조- 힙(Heap)

치맨·2023년 1월 16일
자료구조
0

알고리즘,자료구조

목록 보기
9/11
post-thumbnail

목차

Heap이란

  • 최댓값이나 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조입니다. 트리란? ←

  • 시간복잡도가 삽입,삭제 모두 O(nlog₂n) 입니다.

  • 힙은 반 정렬 상태, 느슨한 정렬 상태 ,약한 힙(weak heap)이라고도 불리는데 이유는 부모노드와 자식노드간의 관계만 신경쓰면 되기 때문에 형제 간 우선순위는 고려되지 않기 때문입니다.

  • 힙(Heap)에는 최소힙과 최대힙이 있습니다.

    • 최소힙 : 작은 값을 항상 트리의 위에 있게 해서 트리의 루트에는 가장 작은 값이 오도록 하는것 입니다.

    • 최대힙 : 최소힙과 반대로 가장 큰 값이 맨 위에 오도록 하여 트리의 루트에는 가장 큰 값이 오도록 하는 것 입니다. 따라서 모든 노드는 자기 부모 노드가 자기보다 큰 값을 가지고 있습니다.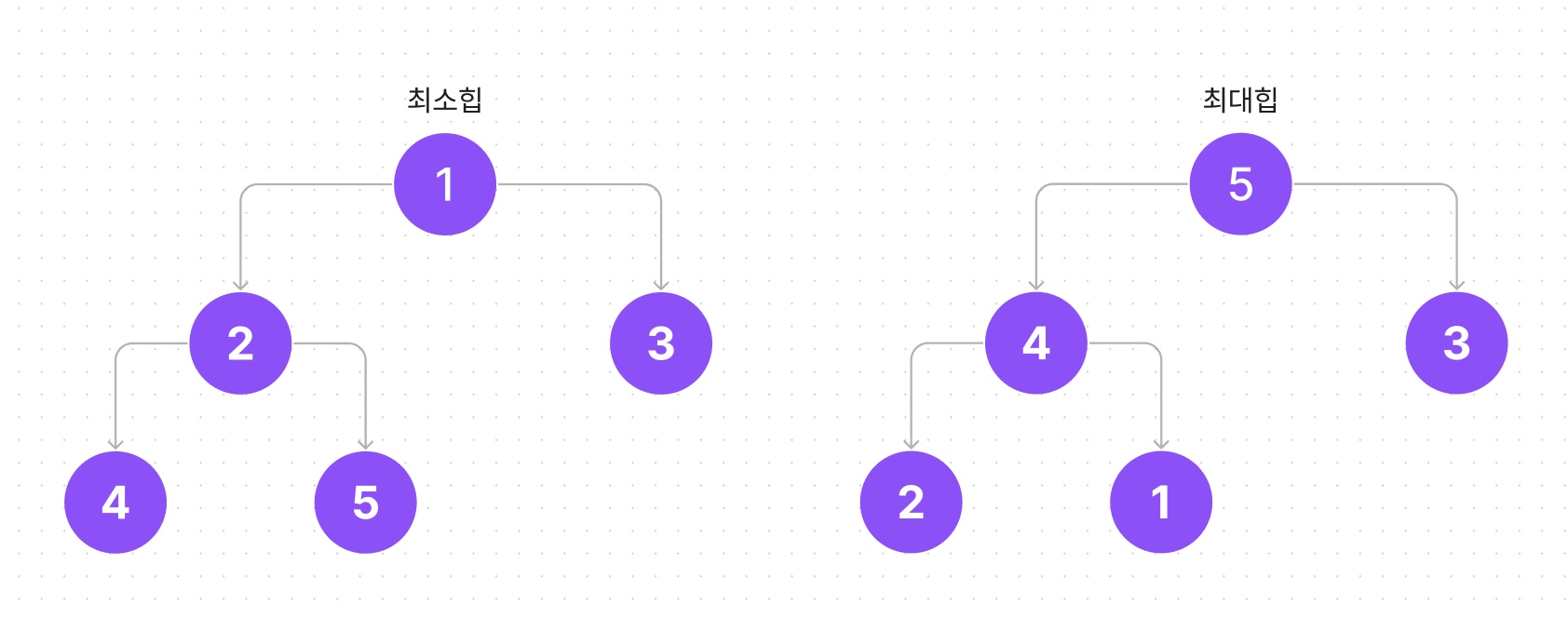

Heap 사용 이유

  • 삽입과 삭제의 시간복잡도가 O(nlog₂n) 즉 효율적이기 때문에 Heap을 사용합니다.

  • 그러면 완전이진트리를 사용하면 되지 왜 힙을 사용할까? 라는 의문이 생겼습니다. 이유는 Heap은 완전 이진 트리보다 수행 속도가 빠르고, 공간을 적게 차지하기 때문에최소/ 최대 값의 확인 및 삭제가 필요할 때는 Heap을 사용합니다.

  • 결론은 삽입과 삭제의 경우 효율적이기 때문에 Heap을 사용합니다.

Heap에 삽입과 삭제

최대힙과 최소힙의 원리는 같으며, 최대힙과 최소힙은 숫자만 반대로 되어 있습니다. 따라서 최소힙만 구현 해보겠습니다.

최소힙 삽입

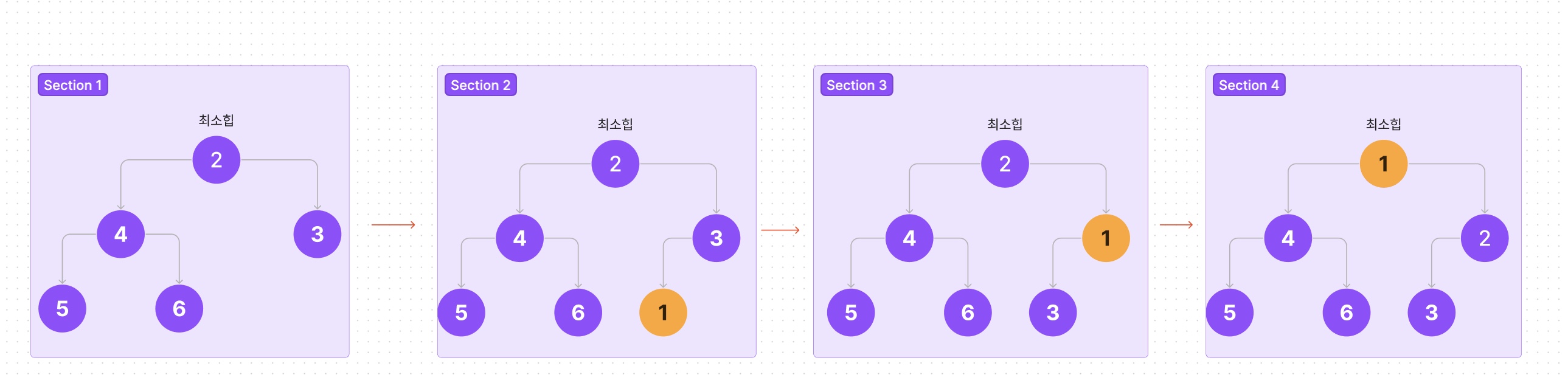
  1. 새로 추가할 노드를 맨 마지막 레벨의 왼쪽부터 넣어줍니다.
  2. 자신(1)과 부모노드(3)를 비교하여 부모노드의 값보다 작다면 바꿔줍니다.
  3. 2번 작업을 반복하여, 자신의 값이 부모노드값보다 작거나 자신의 값이 루트에 도착할 때까지 반복합니다.

이때 부모노드와 비교해서 값을 교환하여 올바르게 정렬이 될 때 까지 올라가는 것을 bubbleUp이라 합니다.

최소힙 삭제

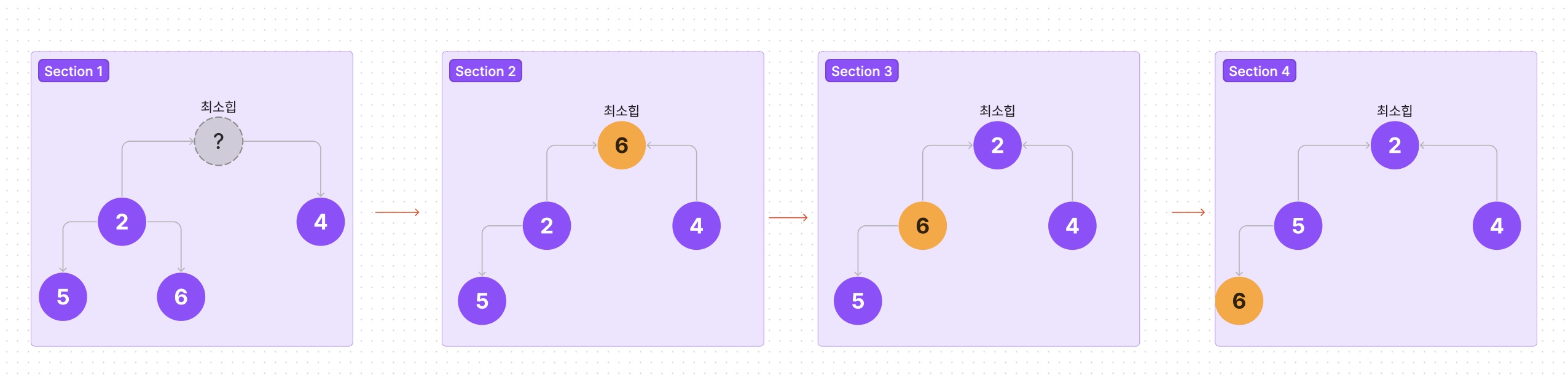
  1. 최소값을 빼줍니다.
  2. 루트노드가 비어있을때, 마지막 값인 6을 루트노드로 가져옵니다.
  3. 자신(6)을 자식노드(2)와 비교해서 작은값이면 바꿔줍니다.
  4. 3번 작업을 반복하여 자식노드가 자신보다 크거나, 마지막 레벨인 경우 멈춰줍니다.

이때 부모노드와 비교해서 값을 교환하여 올바르게 정렬이 될 때 까지 내려가는 것을 bubbleDown이라 합니다.

JS로 Heap 구현

heap을 배열로 구현해보겠습니다. 왜 why? 마지막값을 찾아야 되기 때문에, index를 가지고 있는 배열을 통해 구현하는것이 효율적입니다.

Heap ADT

메소드설명
swap(index1, index2)index1, index2의 값을 바꿔줍니다.
parentIndex(index)부모Node의 index값을 구해줍니다
leftChildIndex(index)왼쪽 자식 노드의 index값을 구해줍니다.
rightChildIndex(index)오른쪽 자식 노드의 index값을 구해줍니다.
parentNode(index)부모 노드의 값을 구해줍니다.
leftChildNode(index)왼쪽 자식 노드의 값을 구해줍니다.
rightChildNode(index)오른쪽 자식 노드의 값을 구해줍니다.
peek()heap의 최상위 노드를 구해줍니다.
size()heap의 크기를 구해줍니다.

class Heap {
  constructor() {
    this.items = [];
  }

  swap(index1, index2) {
    let temp = this.items[index1]; // items의 index1의 값을 temp 담아줍니다.

    this.items[index1] = this.items[index2]; // index2를 index1에 담아줍니다.

    this.items[index2] = temp; // index2에 temp에 옮겨놨던 처음 index1의 값을 담아줍니다.
  }

  parentIndex(index) {
    return Math.floor((index - 1) / 2);
  }

  leftChildIndex(index) {
    return index * 2 + 1;
  }

  rightChildIndex(index) {
    return index * 2 + 2;
  }

  parentNode(index) {
    return this.items[this.parentIndex(index)];
  }

  leftChildNode(index) {
    return this.items[this.leftChildIndex(index)];
  }

  rightChildNode(index) {
    return this.items[this.rightChildIndex(index)];
  }

  peek() {
    return this.items[0];
  }

  size() {
    return this.items.length;
  }
}

JS로 Min Heap 구현

Min Heap ADT : Heap Class를 상속받았기 때문에 Heap메소드도 사용가능

메소드설명
swap(index1, index2)index1, index2의 값을 바꿔줍니다.
parentIndex(index)부모Node의 index값을 구해줍니다
leftChildIndex(index)왼쪽 자식 노드의 index값을 구해줍니다.
rightChildIndex(index)오른쪽 자식 노드의 index값을 구해줍니다.
parentNode(index)부모 노드의 값을 구해줍니다.
leftChildNode(index)왼쪽 자식 노드의 값을 구해줍니다.
rightChildNode(index)오른쪽 자식 노드의 값을 구해줍니다.
peek()heap의 최상위 노드를 구해줍니다.
size()heap의 크기를 구해줍니다.
--
bubbleUp()부모의 노드와 현재의 노드를 바꿔줍니다.
bubbleDown()현재의 노드와 자식의 노드를 바꿔줍니다.
push(item)노드를 추가 해줍니다.
poll()최솟값을 가져옵니다.
class MinHeap extends Heap {
  bubbleUp() {
    let index = this.items.length - 1;

    while (this.parentNode(index) !== undefined && this.parentNode(index) > this.items[index]) {
      this.swap(index, this.parentIndex(index));

      index = this.parentIndex(index);
    }
  }

  bubbleDown() {
    let index = 0;

    while (
      this.leftChildNode(index) !== undefined &&
      (this.leftChildNode(index) < this.items[index] ||
        this.rightChildNode(index) < this.items[index])
    ) {
      let smallerIndex = this.leftChildIndex(index);

      if (
        this.rightChildNode(index) !== undefined &&
        this.rightChildNode(index) < this.items[smallerIndex]
      ) {
        smallerIndex = this.rightChildIndex(index);
      }

      this.swap(index, smallerIndex);

      index = smallerIndex;
    }
  }

  // 힙에 노드를 추가

  push(item) {
    this.items[this.items.length] = item;
    this.bubbleUp();
  }

  // 최소 힙이라면 최솟값이, 최대힙이라면 최댓값을 나타낸다.

  poll() {
    let item = this.items[0]; // 첫번째 원소 keep
    if (item === undefined) {
      return 'Heap이 비어있습니다';
    }
    this.items[0] = this.items[this.items.length - 1]; // 맨 마지막 원소를 첫번째 원소로 복사
    this.items.pop(); // 맨 마지막 원소 삭제
    this.bubbleDown();
    return item;
  }
}

const minheap = new MinHeap();
minheap.push(2);
minheap.push(4);
minheap.push(3);
minheap.push(5);
minheap.push(6);
minheap.push(1);
console.log(minheap); // MinHeap { items: [1, 4, 2, 5, 6, 3 ] }

console.log(minheap.poll()); // 1
console.log(minheap.poll()); // 2
console.log(minheap.poll()); // 3
console.log(minheap.poll()); // 4
console.log(minheap.poll()); // 5
console.log(minheap.poll()); // 6
console.log(minheap.poll()); // Heap이 비어있습니다.

JS로 Max Heap 구현

Max Heap ADT : Heap Class를 상속받은 Min Heap을 상속받아, Heap Class의 메소드와 Min Heap Class를 모두 사용할 수 있지만, Max Heap의 bubbleUp, bubbleDown메소드를 재정의(overriding)해서 사용합니다.

메소드설명
swap(index1, index2)index1, index2의 값을 바꿔줍니다.
parentIndex(index)부모Node의 index값을 구해줍니다
leftChildIndex(index)왼쪽 자식 노드의 index값을 구해줍니다.
rightChildIndex(index)오른쪽 자식 노드의 index값을 구해줍니다.
parentNode(index)부모 노드의 값을 구해줍니다.
leftChildNode(index)왼쪽 자식 노드의 값을 구해줍니다.
rightChildNode(index)오른쪽 자식 노드의 값을 구해줍니다.
peek()heap의 최상위 노드를 구해줍니다.
size()heap의 크기를 구해줍니다.
--
bubbleUp()부모의 노드와 현재의 노드를 바꿔줍니다.
bubbleDown()현재의 노드와 자식의 노드를 바꿔줍니다.
push(item)노드를 추가 해줍니다.
poll()최댓값을 가져옵니다.

class MaxHeap extends MinHeap {
  bubbleUp() {
    let index = this.items.length - 1;
    while (this.parentNode(index) !== undefined && this.parentNode(index) < this.items[index]) {
      this.swap(index, this.parentIndex(index));
      index = this.parentIndex(index);
    }
  }

  bubbleDown() {
    let index = 0;

    while (
      this.leftChildNode(index) !== undefined &&
      (this.leftChildNode(index) > this.items[index] ||
        this.rightChildNode(index) > this.items[index])
    ) {
      let largerIndex = this.leftChildIndex(index);
      if (
        this.rightChildNode(index) !== undefined &&
        this.rightChildNode(index) > this.items[largerIndex]
      ) {
        largerIndex = this.rightChildIndex(index);
      }
      this.swap(largerIndex, index);
      index = largerIndex;
    }
  }
}

const maxheap = new MaxHeap();
maxheap.push(2);
maxheap.push(1);
maxheap.push(4);
maxheap.push(3);
maxheap.push(6);
maxheap.push(5);
console.log(maxheap); // MaxHeap { items: [6,4,5,1,3,2] }

console.log(maxheap.poll()); // 1
console.log(maxheap.poll()); // 2
console.log(maxheap.poll()); // 3
console.log(maxheap.poll()); // 4
console.log(maxheap.poll()); // 5
console.log(maxheap.poll()); // 6
console.log(maxheap.poll()); // Heap이 비어있습니다.

Ref

profile
치맨
기본기가 탄탄한 개발자가 되자!
이전 포스트

자료구조-트리(Tree)

다음 포스트

정렬 알고리즘 - 선택 정렬, 삽입정렬, 버블정렬

0개의 댓글