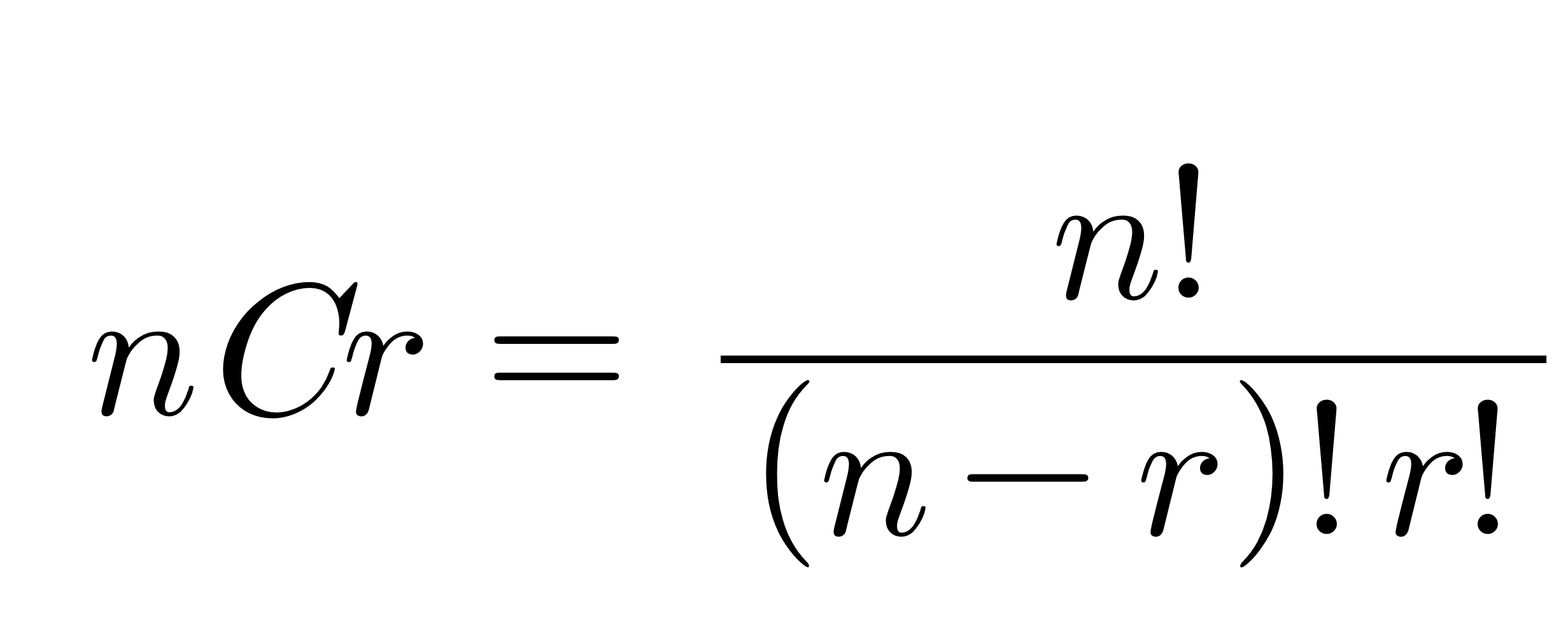 조합은 위의 공식으로 계산합니다. 하지만 여러분은 이 공식을 쓰지않고 다음공식을 사용하여 재귀를 이용해 조합수를 구해주는 프로그램을 작성하세요.
조합은 위의 공식으로 계산합니다. 하지만 여러분은 이 공식을 쓰지않고 다음공식을 사용하여 재귀를 이용해 조합수를 구해주는 프로그램을 작성하세요.
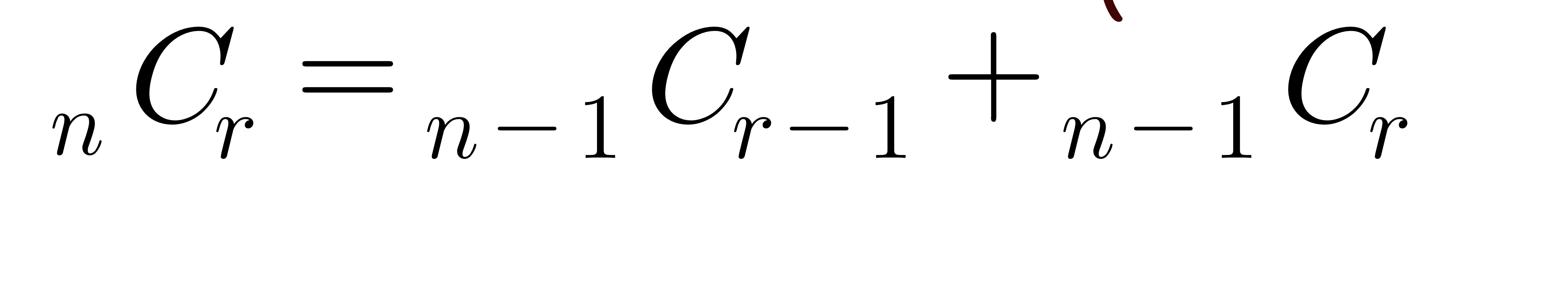
[입력설명]
첫째 줄에 자연수 n(3<=n<=33)과 r(0<=r<=n)이 입력됩니다.
[출력설명]
첫째 줄에 조합수를 출력합니다.
입력예제 1
5 3 (5C3이라는 뜻)
출력예제 1
10
입력예제 2
33 19
출력예제 2
818809200
문제 풀이
예습이론
- 메모이제이션: 이미 구했던 것은 메모를 해놓고, 필요할 때 값을 가져온다. 이를 통해 시간을 매우 줄일 수 있다.
- 문제에서 나온 공식 이해
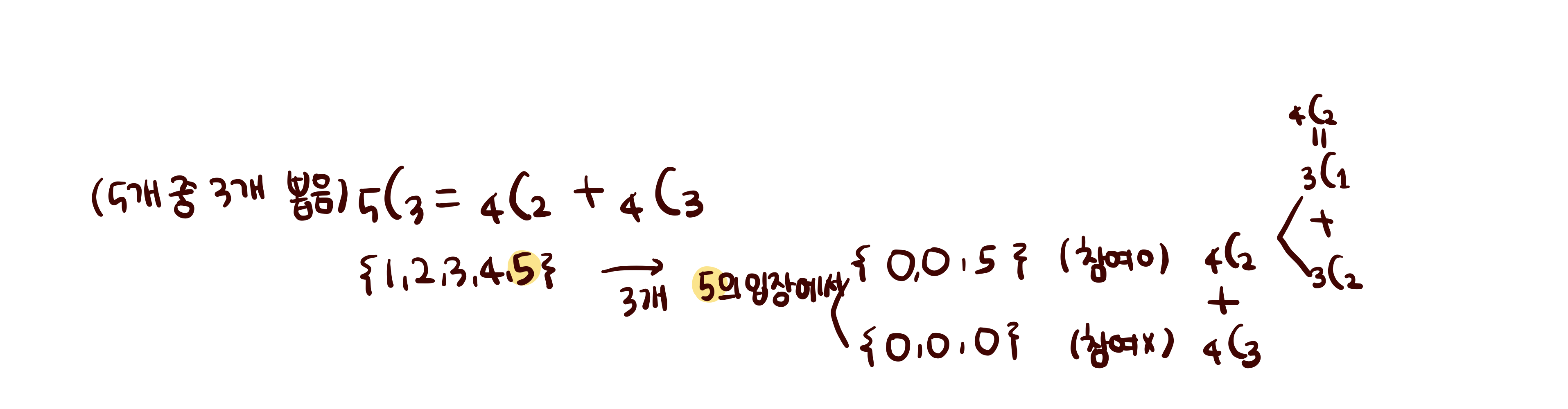
코드
- 문제 풀이 원리는 다음과 같다.
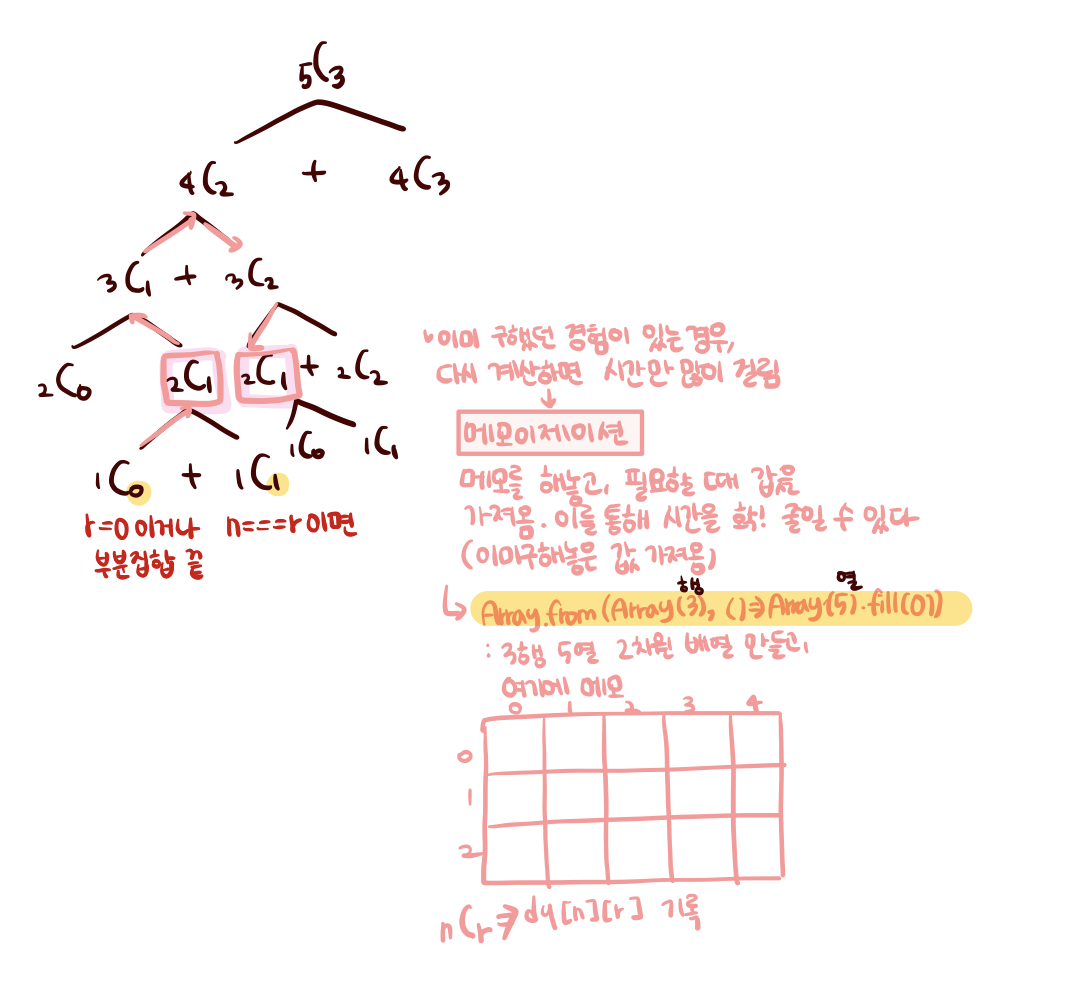
- n, r의 조건에 따라 넉넉잡아 dy를 35행 35열의 유사 배열로 만들어준다.
<!-- 메모이제이션 사용(시간로딩 극복, 권장) -->
<html>
<head>
<meta charset="UTF-8">
<title>출력결과</title>
</head>
<body>
<script>
function solution(n, r){
let answer=[];
let dy=Array.from(Array(35), ()=>Array(35).fill(0)); //35행 35열 배열 만듦
//console.log(dy); //표 확인
function DFS(n, r){
if(dy[n][r]>0) return dy[n][r];//이미 기록이 되어있는 값: 재귀해서 다시 계산 할 필요 없음
if(n===r || r===0) return 1;
else return dy[n][r]=DFS(n-1, r-1)+DFS(n-1, r);
}
answer=DFS(n, r);
return answer;
}
console.log(solution(33, 19));
</script>
</body>
</html>
<!--시간 로딩 너무 많이 걸림(메모이제이션 사용하지 않고 부딪힐때마다 구함)-->
<!--
<html>
<head>
<meta charset="UTF-8">
<title>출력결과</title>
</head>
<body>
<script>
function solution(n, r){
let answer=[];
function DFS(n, r){
if(n===r || r===0) return 1;
else return DFS(n-1, r-1)+DFS(n-1, r);
}
answer=DFS(n, r);
return answer;
}
console.log(solution(5, 3)); //시간 로딩이 너무 많이 걸림
console.log(solution(33, 19)); //시간 로딩이 너무 많이 걸림
</script>
</body>
</html>
-->

9/17
메모이제이션 사용해서 효율성 높이기