파이썬 자료구조 2

알고리즘과 친해지기

알고리즘의 시간, 공간 복잡도를 비교하기 위해 아래 예제를 먼저 확인한다.

• 문제1) 배열 내에서 가장 큰 수를 반환하시오

"""
방법1) 각 숫자마다 다른 모든 숫자와 비교해서 최대값인지 확인. 만약 다른 모든 값보다 크다면
반복문 종료
"""
def find_max_num(array):
    for num in array:
        for c_num in array:
            if num < c_num:
                break
        else:
            return num

print(find_max_num([3, 5, 6, 1, 2, 4])) 
"""
출력 6
"""

"""
방법2) 배열 내 가장 큰 수를 저장할 변수를 만들고, 배열을 돌아가면서 변수와 비교. 
만약 값이 더 크다면,그 변수에 대입.
"""
def find_max_num(array):
    max_num = array[0]
    for num in array:
        if num > max_num:
            max_num = num
    return max_num

print(find_max_num([3, 5, 6, 1, 2, 4]))
"""
출력 6
"""

• 문제2) 문자열을 입력받았을 때, 어떤 알파벳이 가장 많이 포함되어 있는지 반환하시오

"""
방법1) 각 알파벳마다 문자열을 돌면서 몇 글자 나왔는지 확인. 만약 그 숫자가 저장한 알파벳 빈도 수보다 크다면,
그 값을 저장하고 제일 큰 알파벳으로 저장
"""

def find_alphabet_occurrence_array(string):
    alphabet_array = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s",
                      "t", "u", "v", "x", "y", "z"]
    max_oc = 0  #최대 빈도
    max_alp = alphabet_array[0] #최대 알파벳
    for a in alphabet_array: #알파벳 배열에서의 a
        oc = 0
        for char in string: #입력받은 문자열 중
            if char == a: #문자열에 알파벳 원소가 있으면
                oc += 1 #빈도 += 1

        if oc > max_oc:
            max_oc = oc
            max_alp = a
    return  max_alp

print(find_alphabet_occurrence_array("Hello my name is sparta"))

"""
방법2) 각 알파벳의 빈도수를 alp_oc_list 라는 변수에 저장.
각 문자열을 돌면서 해당 문자가 알파벳인지 확인. 알파벳을 인덱스화 시켜 각 알파벳의
빈도수를 업데이트
"""

def find_alphabet_occurrence_array(string):
    alp_oc_array = [0]*26
    for char in string:
        if not char.isalpha():
            continue
        arr_index = ord(char) - ord('a')
        alp_oc_array[arr_index] += 1

    max_oc = 0
    max_alp_index = 0
    for index in range(len(alp_oc_array)):
        alp_oc = alp_oc_array[index]
        if alp_oc > max_oc:
            max_oc = alp_oc
            max_alp_index = index
    return chr(max_alp_index + ord('a'))

print(find_alphabet_occurrence_array("Hello my name is sparta"))

시간 복잡도

시간 복잡도: 입력값과 문제를 해결하는 데 걸리는 시간과의 상관관계

각 줄이 실행되는 걸 1번의 연산이 된다고 생각하고 계산하자면
첫 번째 문제의 방법 1

for num in array: #array의 길이만큼 아래 연산 실행 
        for c_num in array: #array의 길이만큼 아래 연산 실행 
            if num < c_num: #비교 연산 1번 실행 
                break
        else:
            return num

array x array x 1
즉, N x N

첫 번째 문자의 방법2

  max_num = array[0] #연산 1번 실행 
    for num in array: #array의 길이만큼 아래 연산 실행 
        if num > max_num: #비교 연산 1번 실행 
            max_num = num #비교 연산 1번 실행 
    return max_num 

1 + array X (1+1)
= 2N + 1

비교)

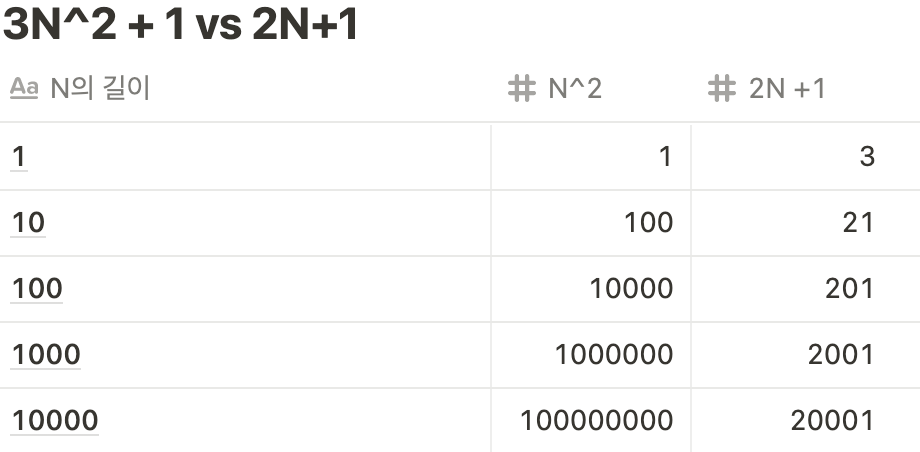
👉 하지만 매번 코드를 매 실행 단위로 이렇게 몇 번의 연산이 발생하는지 확인하는 건 불가능. 따라서 상수는 신경쓰지말고, 입력값에 비례해서 어느 정도로 증가하는지만 파악하기

공간 복잡도 판단하기

공간 복잡도란 입력값과 문제를 해결하는 데 걸리는 공간과의 상관관계

저장하는 데이터의 양이 1개의 공간 사용
두 번째 문제 방법1)

    alphabet_array = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "x", "y", "z"]
#26 개의 공간을 사용합니다
    max_occurrence = 0 # 1개의 공간을 사용합니다
    max_alphabet = alphabet_array[0]   # 1개의 공간을 사용합니다.

    for alphabet in alphabet_array:
        occurrence = 0  # 1개의 공간을 사용합니다

26 + 1 + 1 + 1 = 29개의 공간 사용

두 번째 문제 방법2)

 alphabet_occurrence_list = [0] * 26 #26개 

    for char in string:
        if not char.isalpha():
            continue
        arr_index = ord(char) - ord('a') #1개
        alphabet_occurrence_list[arr_index] += 1 

    max_occurrence = 0 #1개
    max_alphabet_index = 0 #1개 
    for index in range(len(alphabet_occurrence_list)):
        alphabet_occurrence = alphabet_occurrence_list[index] #1개
        if alphabet_occurrence > max_occurrence:
            max_occurrence = alphabet_occurrence 
            max_alphabet_index = index 

    return chr(max_alphabet_index + ord('a'))

26 + 4 = 30개

✅ 29나 30 모두 상수라 큰 차이는 없다. 이럴 땐 시간 복잡도로 비교하는데 더 좋다. 대부분의 문제에서는 알고리즘의 성능이 공간에 의해서 결정되지 않는다. 따라서 공간 복잡도 보다는 시간 복잡도를 더 신경 써야 한다

두 번째 문제 방법1)

for alphabet in alphabet_array:    
         # alphabet_array 의 길이(26)만큼 아래 연산이 실행
        occurrence = 0                  # 대입 연산 1번 실행
        for char in string:             # string 의 길이만큼 아래 연산이 실행
            if char == alphabet:        # 비교 연산 1번 실행
                occurrence += 1         # 대입 연산 1번 실행 

        if occurrence > max_occurrence: # 비교 연산 1번 실행
            max_alphabet = alphabet     # 대입 연산 1번 실행
            max_occurrence = number     # 대입 연산 1번 실행

array x 1 + string x (2) + 3
= 26 (1+2N+3) = 52N + 104

두 번째 문제 방법2)

  for char in string:        # string 의 길이만큼 아래 연산이 실행
        if not char.isalpha(): # 비교 연산 1번 실행
            continue
        arr_index = ord(char) - ord('a')         # 대입 연산 1번 실행 
        alphabet_occurrence_list[arr_index] += 1 # 대입 연산 1번 실행 

    max_occurrence = 0        # 대입 연산 1번 실행 
    max_alphabet_index = 0    # 대입 연산 1번 실행 
    for index in range(len(alphabet_occurrence_list)):    # alphabet_array 의 길이(26)만큼 아래 연산이 실행
        alphabet_occurrence = alphabet_occurrence_list[index] # 대입 연산 1번 실행 
        if alphabet_occurrence > max_occurrence: # 비교 연산 1번 실행 
            max_occurrence = alphabet_occurrence # 대입 연산 1번 실행 
            max_alphabet_index = index           # 대입 연산 1번 실행 

string x (1+2) + 1 + 1 + array x (1+3)
3N + 2 + 26(4)
=3N + 2 + 104
= 3N + 106

👉 다른 상수 시간의 연산은 계산하지 않아도 되기 때문에 N 만큼의 시간이 필요하다고 생각하면 된다

점근 표기법

알고리즘의 성능을 수학적으로 표기하는 방법
빅오(Big-O), 빅오메가(Big-Ω)
빅오는 최악의 성능이 나올 때 어느 정도의 연산량이 걸릴 것인지, 빅 오메가는 최선의 성능이 나올 때 어느 정도의 연산량이 걸릴 것인지에 대해 표기

빅오 표기법으로 표시하면 $O(N)$,
빅 오메가 표기법으로 표시하면 $Ω(1)$

#배열 내에 특정 숫자가 존재한다면 True, 존재하지 않다면 False 를 반환
def is_number_exist(number, array):
    for i in array: #array의 길핻만큼 아래 연산 진
        if number == i: #비교 연산 1번 
            return True
    return False
result = is_number_exist
print(result(3,[3,5,6,1,2,4]))

-> N x 1의 시간 복잡도

🔰 알고리즘의 성능은 항상 동일한 게 아니라 입력값에 따라서 달라질 수 있다. 어떤 값을 가지고 있는지, 어떤 패턴을 이루는 데이터인지에 따라서 뭐가 좋은 알고리즘인지 달라질 수 있다

알고리즘에서는 거의 모든 알고리즘을 빅오 표기법으로 분석한다. 대부분의 입력값이 최선의 경우일 가능성은 굉장히 적을 뿐더러, 우리는 최악의 경우를 대비해야 하기 때문

알고리즘 더 풀어보기

"""
숫자 사이에 '✕' 혹은 '+' 연산자를 넣어 결과적으로 가장 큰 수를 구하는 프로그램을 작성하시오
"""
def find_max_plus_or_multiply(array):
    multiple_sum = 0
    for i in array:
        if i <= 1 or multiple_sum <= 1:
            multiple_sum += i
        else:
            multiple_sum *= 1
    return multiple_sum

result = find_max_plus_or_multiply  #시간 복잡도: O(N)
print("정답 = 728 현재 풀이 값 =", result([0,3,5,6,1,2,4]))

"""
문자열에서 반복되지 않는 첫번째 문자를 반환하시오.
"""
input = "abadabac"

def find_not_repeating_first_character(string):
    alphabet_occurrence_array = [0] * 26

    for char in string:       #빈도 확인 
        if not char.isalpha():
            continue
        arr_index = ord(char) - ord("a")
        alphabet_occurrence_array[arr_index] += 1

    not_repeating_character_array = [] #반복되지 않는 문자열 찾기 
    for index in range(len(alphabet_occurrence_array)):
        alphabet_occurrence = alphabet_occurrence_array[index]

        if alphabet_occurrence == 1:
            not_repeating_character_array.append(chr(index + ord("a")))

    for char in string:
        if char in not_repeating_character_array:
            return char #첫 번째 문자 반환 

    return "_"

#시간 복잡도: O(N)
result = find_not_repeating_first_character
print("정답 = d 현재 풀이 값 =", result("abadabac"))

#소수 나열하기  
input = 20

def find_prime_list_under_number(number):
    prime_list = []

    for n in range(2, number+1):
        for i in prime_list:
            if n % i == 0 and i * i <= n:
                break
        else:
            prime_list.append(n)
    return prime_list

result = find_prime_list_under_number(input)
print(result)

#문자열 뒤집기
input = "011110"

def find_count_to_turn_out_to_all_zero_or_all_one(string):
    count_to_all_zero = 0
    count_to_all_one = 0

    if string[0] == '0':
        count_to_all_one += 1
    elif string[0] == '1':
        count_to_all_zero += 1

    for i in range(len(string) - 1):
        if string[i] != string[i + 1]:
            if string[i + 1] == '0':
                count_to_all_one += 1
            if string[i + 1] == '1':
                count_to_all_zero += 1

    return min(count_to_all_one, count_to_all_zero)

result = find_count_to_turn_out_to_all_zero_or_all_one(input)
print(result)

🔥 부족한 점

개념과 코드를 이해하는 건 어렵지 않은데 아직 문제만 주어졌을 때 코드를 완벽하게 구상하지 못한다.
더 많은 예제 문제를 풀어보며 코드를 구성해 나갈 수 있는 힘을 길러야겠다.